体会变化过程 培养直观想象

甘肃 张建文

直观想象素养是高中数学六大核心素养之一,而空间图形是培养学生直观想象素养的主要素材.直观想象包括图形的构建与分解,还包括利用图形进行的相关推理与运算.本文依托不同的图形情境,重点举例说明空间图形中的变化问题、函数问题、轨迹问题、截面问题以及最值问题等.依托空间图形进行学生直观想象素养的培养重在以问导学、以题引路,使得学生在感受图形变化的同时,学会反思总结.下面笔者就依托空间图形训练学生直观想象，并进行实例简述.

1.折叠中的变化问题

( )

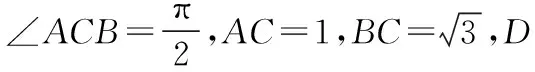
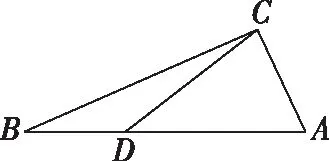
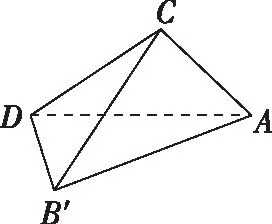
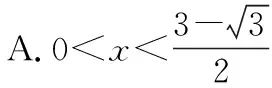
分析:此题是训练或考查学生直观想象素养的良好素材,包含图形的动态变化过程,涉及变量的有效选择,不等式的构造.解答的关键在于控制变量单独分析.

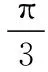
问题1.体会翻折过程，我们怎么将D在AB上的位置转化为角度？(设∠BCD=α)

问题2.在B′C变化的过程中，异面直线B′C与AD的夹角如何用图形直观表示？

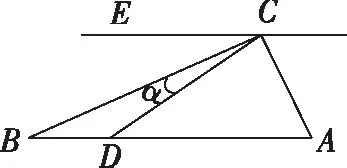
问题3.异面直线B′C与AD的夹角是如何刻画的？

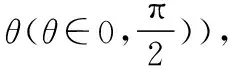
问题4.在翻折过程中θ和∠B′CE是连续变化的吗？

问题5.可以明确说明θ和∠B′CE的变化关系吗？

问题7.那临界状态是什么？

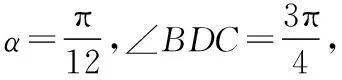
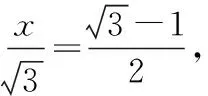
问题8.通过此练习题你有什么收获？(旨在促进学生进行反思)

学生总结：①要体会图形的折叠过程，从中发现解决问题的突破口；

②要理解变与不变的辩证关系，变化中有不变，不变中有变化；

启示：以问题促进学生思维发展，可以引导学生找准思维基点，发现知识的联系点，在学生会与不会处设置引导性问题，助力学生形成良好的思维习惯，获得思维经验，培养辩证思维和数学核心素养.

2.变动中的函数问题

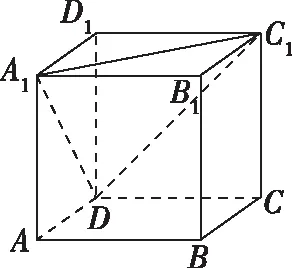
例2.如图为正方体ABCD-A1B1C1D1，动点M从点B1出发，在正方体表面沿逆时针方向运动一周后,再次回到B1的运动过程中,点M与平面A1DC1的距离保持不变,运动的路程x与l=MA1+MC1+MD之间满足函数关系式l=f(x),则此函数图象大致是

( )

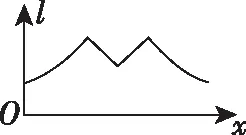
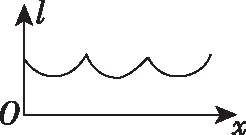
分析：体会动点M的运动过程，确定点M的运动轨迹,从中直观感受点M与三点A1,D,C1的距离变化,体会在点M运动变化过程中的变化与不变.

师生互动过程：在引导学生确定点M的运动轨迹后,找准学生的思维障碍点,以问题为索引引导学生进行量化分析,掌握通性通法,特别是选择题的解答方法,最后引导学生进行自我评价和总结,达到触类旁通的效果.

问题1.如何理解题目中的“点M与平面A1DC1的距离保持不变”？

问题2.体会动点M的运动过程,能画出动点M的轨迹吗？

学生操作：以线面平行的判定定理为依据,在平面ABB1A1内,过B1有B1A∥平面A1DC1，

同理可得AC∥平面A1DC1,CB1∥平面A1DC1,所以动点M的轨迹是△B1AC的三边.

问题3.设正方体的棱长是1,根据题型来看,要构造函数还是取特殊点分析比较好.

学生思考：取特殊点分析验证,排除不合理选项.

问题4.取哪些特殊点进行？

问题5.通过此题的解答你有什么收获？

学生总结：①选择题的解答应该是小题巧做,不要小题大做;

②此题的“题眼”是动点的轨迹，解题方法是排除法；

③在变化中构造函数关系,体会变化与不变的辩证关系.

启示：课堂上的解题教学要以问题背景为情境，通过恰到好处的问题引导使得学生思维能够经历整个分析过程，体会动点的运动过程，直观感受变动过程中的各种数量关系，为问题的有效解决提供方向．这使得学生能抓住问题的本质，进而产生“顿悟”.

3.空间轨迹判断:转化与化归

例3.已知异面直线a,b的夹角是60°,其公垂线段为EF,|EF|=2,长为4的线段AB的两端分别在直线a,b上运动,则AB中点的轨迹为

( )

A.椭圆 B.双曲线

C.圆 D.以上都不是

分析：此题属于立体几何中的动点轨迹判断问题,关键要合理作图,在图形中观察出线段之间的数量关系,将空间动点转化为平面内动点问题,建立恰当的坐标系解决问题.

师生互动过程：在通读题目的基础上,引导学生在脑海中想象线段AB的运动过程,体会AB中点P的运动过程,大致确定动点P所在的平面.之后引导学生画出简图,将问题转化为平面内动点的轨迹问题,最后通过定义确定曲线或选择方程确定曲线解决问题．

问题1.你能直观感受到AB中点P的轨迹吗?

学生思考:在脑海中感受图形的运动过程.

问题2.你可以画出简图进行量化分析吗？

学生操作：设EF的中点为O，过O作EF的垂面α，

可知AB中点P必在面α上，同时设M,N为A,B在平面α内的射影点.

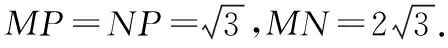
问题3.原问题可以进行怎样转化？

学生操作:可以将问题转化为“已知在平面α内,两直线之间的夹角是60°,且相交于点O,M,N是两直线上的两个动点,判断M,N中点P的轨迹.”

问题4.通常情况下,我们是怎么判断动点的轨迹问题的？

学生思考：根据定义或是借助方程.

问题5.若是借助方程,该怎么求解点P的轨迹方程？

学生操作：在平面α内建立坐标系,求出动点P的轨迹方程.

问题6.怎么建系比较好？为什么？

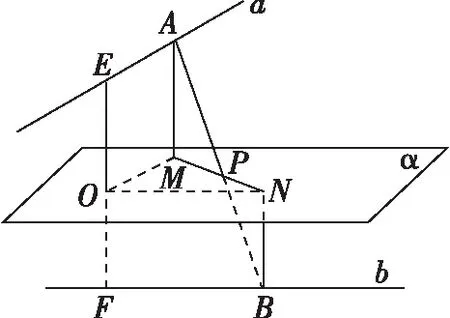
学生操作：以O为坐标原点,∠MON的角平分线为x轴,建立平面直角坐标系,如图所示.这样建系可以得到标准方程,便于判断轨迹.

问题7.如何建立点P的坐标与MN之间的关系？

学生操作：设OM=m,ON=n,由余弦定理可知,MN2=12=m2+n2-2mncos60°,

即m2+n2-mn=12(*),

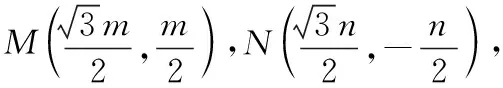
问题8.你从中有什么收获？

学生总结：①空间轨迹问题通常要转化到某个平面内研究；

②轨迹判断问题通常可以通过先求曲线方程再判断轨迹.

启示：转化与化归思想也是立体几何常用到的思想,就是要将空间内比较复杂的问题转化到平面内分析研究.我们研究习题不光是为了掌握知识的应用，更是为了锻炼思维，提高分析问题和解决问题的能力，形成数学思想，培养学生的数学核心素养.

4.空间几何体的截面问题

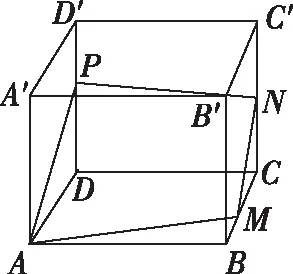
例4.已知正方体的体积为1,点M在线段BC上(点M异于B,C两点),点N为线段CC1的中点,若平面AMN截正方体ABCD-A′B′C′D′所得的截面为四边形,则线段BM的取值范围为

( )

分析：此题属于动态变化中的截面问题,通过点的运动变化，直观想象截面的动态图形并判断其形状.解答的关键在于合理借助图形进行准确作图,找准图形变化的临界状态,抓主抓重.

师生互动过程：教师首先要营造思维环境,引导学生在脑海中直观感受图形的变化过程,其次要作图分析,增强学生的动手能力,找准截面是四边形与五边形的临界状态.最后，再次清晰经历图形的动态变化过程,确定动点M的范围.

问题1.可以作出简图,感受动点M的变化过程吗？

学生操作：根据题意作简图,并让点M在BC上运动,直观想象截面图形.

问题2.可以取特殊点作出四边形截面或五边形截面吗？

学生操作：取靠近B的点M可以得到截面是四边形,取靠近C的点M可以得到截面是五边形.

问题3.截面图形的对边之间有什么关系？对你有什么启示？

学生观察思考：两个平行平面内的直线平行,如四边形中MN∥AP,五边形中MN∥AH,AM∥HQ.由此可知只要作出对应的边，找到对应的点就可以确定截面图形的形状.

问题4.四边形与五边形的临界状态是怎样的？

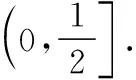
问题5.你从中有什么收获？

学生总结：①截面问题的关键是要确定截面图形的边和顶点;

②思路上的突破要通过取特殊点进行观察比较；

③体会图形变化过程,学会将复杂问题转化为简单问题.

5.空间最值问题

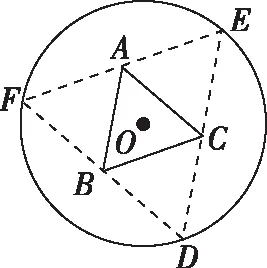
例5.(2017·全国卷Ⅰ理·16)如图，圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位：cm3)的最大值为________.

分析：先体会圆形纸片上剪出来的三棱锥的大小变化过程,大小是由三角形ABC的边长来控制,同时要确定边长为何值时构造的三棱锥的体积最大.要通过观察或构造函数来确定三棱锥的最大体积.

师生互动过程：首先教师引导学生感受图形的变化过程,在脑海中构造三棱锥,并使得三棱锥的大小随着三角形ABC的边长变化而变化;其次尝试探寻求解三棱锥体积最大的方法(构造函数);最后转化为函数问题进行解答.

问题1.你能直观想象三棱锥的形成过程吗？

学生思考：形成的三棱锥是正三棱锥(底面是正三角形，侧棱长都相等),其图形变化始终保持以下三点：①必须是圆形纸板裁剪出来的;②圆心O是三角形ABC的中心;③延伸出来的三角形是等腰三角形.

问题2.三棱锥的体积怎么确定？

问题3.通常通过什么方法来确定一个量的最值？三棱锥的最大体积怎么确定？

学生操作：通常情况下确定一个量最值的方法有观察法和构造函数法.由于三棱锥底面积和高都在变化,通过观察来确定三棱锥的体积最大值行不通,所以只能通过构造函数来实现.

问题4.观察图形,三棱锥的底面边长与高有什么关系？

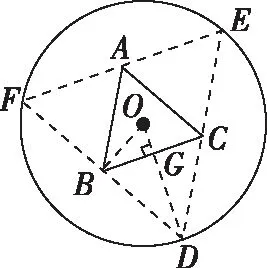
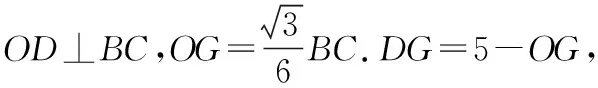
问题5.选择哪个量作为函数的自变量比较好？为什么？

学生操作：从计算过程的简洁度来看,因为每一个量都与OG有直接联系,所以选择OG作为自变量最好.

问题6.怎么来求这个函数的最值？

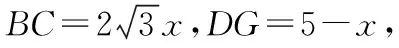
问题7.怎么确定定义域？

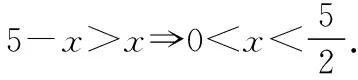
问题8.怎么求三棱锥体积的最大值？

问题9.从中你有什么收获？

学生总结：①要体会图形的变化过程，感受变化中的不变性;

②学会通性通法，掌握最值问题的常见处理方法;

③学会转化与化归思想，将复杂问题简单化.

6.思考与展望