三个“一”引领二轮复习 例题教学落地核心素养

陕西 张教训 韩红军

(作者单位:陕西省麟游县中学)

美国数学家波利亚指出:“拿一个有意义又不复杂的题目去帮助学生发掘问题的各个方面，使得通过这个题目就好像通过一道门户，把学生引入一个完整的领域.”在教学实践中,特别是高三二轮复习阶段，对一个典型问题要引导学生从不同角度分析理解，探索不同的解决方法，努力做到一题多解；对一个有意义的问题不仅要满足得出答案，同时要引导学生对问题进行深入挖掘，适当变式、拓展，特殊化或一般化，从而获得“一题多思”“一题多变”“一题多得”的效果；引导学生对一些“相似、相像、相近”的问题进行梳理、归类，抓住问题的内在联系与主要矛盾，减少机械重复训练，争取达到多题归一的境界.在二轮复习中，课堂教学做到这三点，高考复习效率就会大大提高，真正实现数学核心素养落地生根.

一、一题多解

一题多解，能够使学生开阔思路，把学过的知识和方法融会贯通，使用自如，提升学生分析问题和解决问题的能力.一题多解可以培养学生灵活、敏捷的思维能力，让学生学会对问题进行多角度、多层次的分析，达到对问题的全面理解，进而迅速准确的解决问题.通过一题多解的训练，可以培养学生的发散性思维及联想能力，学会用不同的知识解决同一个问题，达到对多种知识的融会贯通.

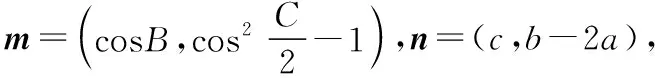
(1)求角C的大小；

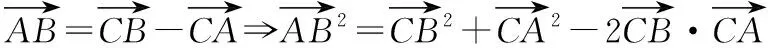
法2:(余弦定理法)在△CAD中，由余弦定理得CA2=CD2+AD2-2CD·AD·cos∠ADC①，在△CBD中，由余弦定理得CB2=CD2+BD2-2CD·BD·cos∠BDC②，

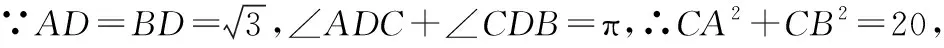
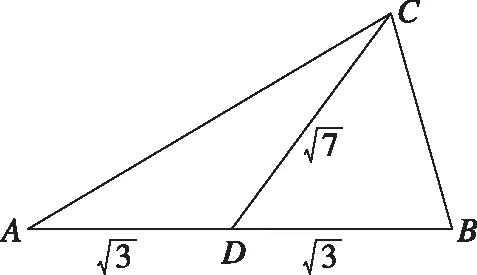
法3:(补形法)如图，将三角形补形成平行四边形，在△CAE中，由余弦定理得CE2=CA2+AE2-2CA·AE·cos∠CAE⟹b2+a2+ab=28①，

在△ABC中，由余弦定理得a2+b2-ab=12②，

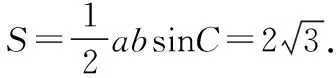
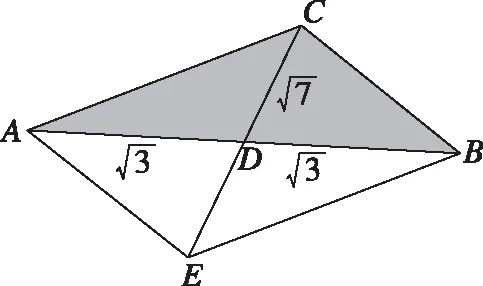
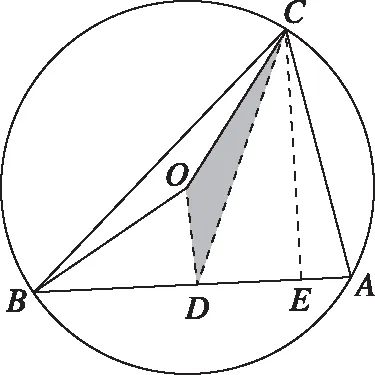
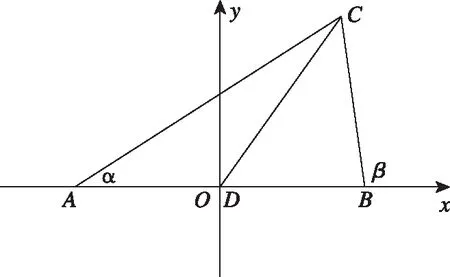
评注:这是一道比较典型的解三角形问题，大部分学生能够把它解出来.如果我们仅仅满足于此，显然就淡化了例题教学的价值.在高三二轮复习中，如何把一道典型试题的教学效果最大化，发挥典型例题的引领作用，是我们每个老师在备考阶段需要深思的问题，也是备课组需要研讨的问题.

二、一题多变

波利亚曾指出:“好问题同某种蘑菇有些相像，它们都成堆地生长，找到一个后，你应当在周围找找，很可能附近就有好几个.”在解题教学活动过程中要学会采“蘑菇”，善于引导学生对一个好问题进行变式改造，如改变题目的条件、结论、图形、叙述方式等，进而对问题进行更深层次的探索，这样灵活的运用变式教学，既可以免于搞题海战术，减轻学生负担，做到深入浅出，以点带面，以少胜多，又能较好地培养学生的思维能力，克服思维定式，提高学生的解题能力及应变能力，从而激发学生学习数学的兴趣，提高学习积极性.

【例2】(2018·全国卷Ⅱ理·21)已知函数f(x)=ex-ax2.

(Ⅰ)若a=1，证明:当x≥0时，f(x)≥1；

(Ⅱ)若f(x)在(0,+∞)只有一个零点，求a.

变式1:已知函数f(x)=ex-ax2，若f(x)≥1在区间[0，+∞)上恒成立，求a的取值范围；

变式2:讨论函数f(x)=ex-ax2的零点个数；

变式3:讨论函数f(x)=ex-ax2(a≥0)的极值点个数；

变式4:若函数f(x)在区间(0，+∞)上有两个极值点x1,x2(0

变式5:若函数g(x)=x-ln(ax2+1)(a>0，x≥0)有两个极值点x1,x2(x1

图书馆的服务不仅服务资源建设，更主要的是服务于人的发展。在图书馆的主页上，链接导师服务，或者组成学习小组或团队。在网络资源的学习过程中，注重对学生的学习支持、图书馆员作为参与者加入课程的辅导教师队伍中，比如发布公告和邮件通知、对学生适时进行学习路径的导航，通过线上、线下的参考咨询或者讨论组解答学生在学习中遇到的问题，帮助他们拓展相关的领域知识。这种做法能够充分体现图书馆的教育功能：连接与合作、网络化学习、融入课程、分享经验等特点。

评注:全国卷Ⅱ摒弃偏题、难题、怪题，注重主干知识，关键能力和核心素养的考查，引导数学教学回归课堂，重视教材.其试题设计充分体现基础性、层次性、实践性.当然对于高三复习备考而言，我们可以对试题进行适当的变式、拓展，拓宽学生的视野，提升学生的思维能力，提高复习的效益.

三、多题归一

在海量的数学试题中，很多问题其实大同小异，形异而神似，即所谓的同一“题型”.在教学过程中，我们要引导学生对它们从知识角度或解法角度进行归纳类比，梳理小结，提高学生对问题的理解与认识水平，强化他们对相关知识、方法的熟练与规范应用，力求做到举一反三，触类旁通，提升复习的效率与应对考试的能力.

1.题型归一

【例3.1】在△ABC中，三个内角A,B，C的对边分别为a,b,c，若m=(cosB,cosC),n=(2a+c,b)，且m⊥n.

(1)求角B的大小；

(1)求角A的值；

(1)求A；

(1)求角A的大小；

(2)若a=2，求△ABC的周长的取值范围.

评注:四道试题大同小异，其实为“同一个”问题.考查了解三角形中的三角恒等变换，利用正、余弦定理，通过边、角互化，求已知三角形的角和边；利用三角形的面积公式、三边之间的关系，三角函数的性质，结合均值不等式等，可求已知三角形的周长或面积的取值范围.解三角形试题难度不大，解题时要注重数形结合、注重分析、重视运算.

2.解法归一

( )

分析:曲线g(x)=f(x)-ax与x轴有三个不同的交点,即函数g(x)有三个不同的零点⟺方程f(x)=ax有三个不同的解⟺曲线y=f(x)与直线y=ax有三个不同的交点.

评注:已知函数图象与x轴的交点个数，求参数的取值范围，相当于已知函数的零点个数或相应的方程的实数根的个数，求参数的取值范围，目的是考查函数的零点、函数与方程的关系，考查数形结合的数学思想方法，考查分析问题、转化问题与解决问题的能力.

【例4.2】已知函数f(x)=ax,g(x)=lnx,a∈R.若在[1，+∞)上不等式xf(x-1)≥g(x)恒成立，求实数a的取值范围.

法2：不等式xf(x-1)≥g(x)即ax(x-1)≥lnx，令h(x)=ax(x-1)，则命题等价于在区间[1，+∞)内，曲线y=h(x)恒在曲线y=g(x)的上方(可以有公共点)，如图.

评注:很多含参不等式成立问题的原始背景就是直线与曲线的位置关系，从这个层面理解直观想象素养，就是让我们清晰地追溯到题目的源泉，站在更高的层面理解不等式问题的本质.并且我们还可以发现:当参数恰为一次项系数时，这个参数往往具备了斜率的几何意义，这就是将不等式转化为直线与曲线位置关系的核心所在.

评注:试题4.1是已知函数的零点个数，求参数的取值范围；试题4.2是已知函数不等式恒成立，求参数的取值范围；试题4.3通过等价转化，化归为直线AP的倾斜角α(α为锐角)的正弦值.因为所求参数有明确的几何意义，比如直线的斜率(倾斜角)，二次函数的二次项系数，而参数的“临界值”恰好是切线斜率，那么我们求解的策略就是巧用相切，化难为易.

将大量的“同类”问题进行恰当地“整合”之后，引导学生进行分析、比较、思考与探究、实践与体会，有利于学生从不同的角度审视问题，促进学生深入问题的内部，排除细枝末节的干扰，透过现象抓住本质，把问题弄清看透，从而提高学生分析问题的能力；有利于学生整体把握问题，形成对该类问题的一个合理成熟的算法，避免求解此类问题时走弯路甚至走死路，达到快捷准确的解题效果，从而提高学生解题的效率与解决问题的能力；也有利于淡化老师搞“题海”战术，避免重复机械训练，耗费学生宝贵的复习时间.