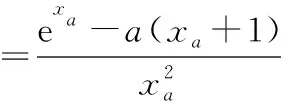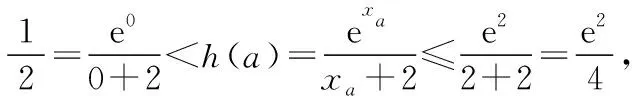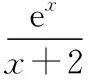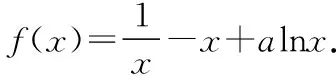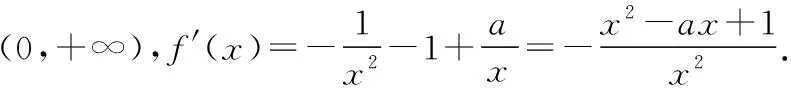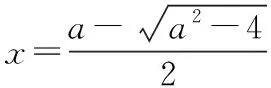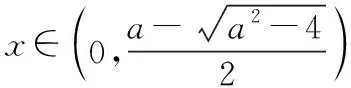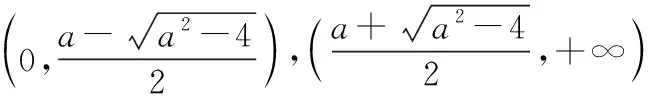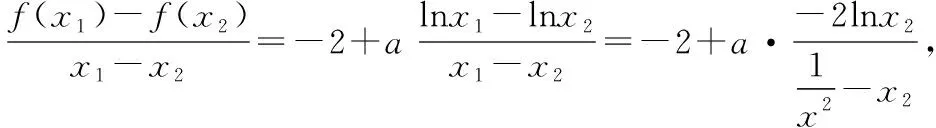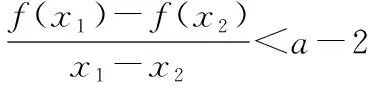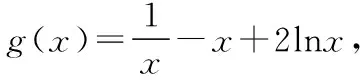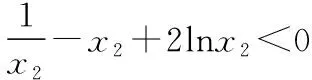导数压轴题常用方法揭秘

福建 林进伟

(作者单位:福建省惠安第一中学)

导数是研究函数性质的重要工具，是高考的重点与难点，在高考中常作为压轴题出现.由于它对思维能力要求高及解题方法灵活、难度大等特点，拿下导数压轴题是取得高分的关键，也是一道难以迈过去的坎.本文就导数压轴题中常见的解题策略及技巧进行系统的梳理和揭秘.

【典型题例】

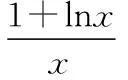
【思路探析】

本题是含参的函数不等式求参数范围的问题，解决这类题目的常规思路是分参.但此题不易分参，而且直接求导后，导函数又含有lnx,ex这两个部分，这就给导函数正负的判断带来了很大的困难.为此，我们采用“对数单身狗，指数找基友”的策略先进行等价变形.

【详解示范】

问题等价于ax+xe-ax-lnx-1≥0恒成立，令f(x)=ax+xe-ax-lnx-1，则f(x)≥0恒成立.

(ⅰ)当a=0时，f(x)=x-lnx-1≥0恒成立，所以a=0满足条件；

又t(1)=ea-1<0，即t(x)在[n,1)中有唯一解x0且eax0=x0.

故只需ymin=f(x0)=ax0+x0e-ax0-lnx0-1≥0，

由eax0=x0，可得x0e-ax0=1,lneax0=ax0=lnx0，即f(x0)=0，

所以a<0满足条件；

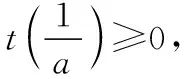
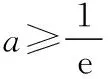
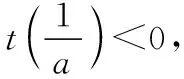
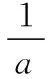
又因为f(xi)=axi+xie-axi-lnxi-1=0(i=1,2)，

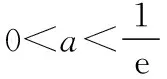
综上，a∈R.

【解后反思】

(3)解题过程中，利用零点的存在性定理说明导数零点的存在，用到了取点的方法，但也可以直接用极限判断图象的变化趋势来说明，同时a=0与a<0可以合在一起讨论.

(4)解题过程中，单调性与最值的确定还用到“隐零点的代换”技巧.即隐零点的处理一般用整体转化、换元或者代换(把复杂部分如指、对数或高次部分换成较简单的式子).

【问题】

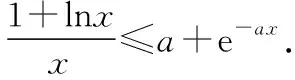
【策略1】由于在式子结构中，与a有关的部分比较简单，于是就视a为主元.

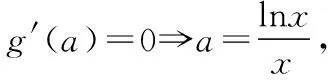
【策略2】利用ex≥x+1放缩法.

问题等价于证明:ax+xe-ax-lnx-1≥0.

由于ax+xe-ax-lnx-1=ax+elnx-ax-lnx-1≥ax+lnx-ax+1-lnx-1=0，

所以原不等式得证.

【反思】由于所证不等式与a相关的部分比较简单，因此策略1采用“视a为主元”的解题策略，可以达到事半功倍的效果.而“放缩法”是基于把指、对数放缩成幂函数，从而降低求导之后判断正负的难度的一种策略，既揭示了命题的意图，又体现了问题的本质，但不易想到.

通过上述典例及问题的探究，基本覆盖了解决导数压轴题中常用的策略与技巧，如指数、对数函数的处理、主元思想、放缩法、隐零点代换等.通过详细地分析与反思，可知其然而且知其所以然.下面再通过几道高考真题来进一步熟悉与巩固这些常用的策略与技巧.

【高考真题】

1.(2015·全国卷Ⅰ文·21)设函数f(x)=e2x-alnx.

(Ⅰ)讨论f(x)的导函数f′(x)的零点的个数；

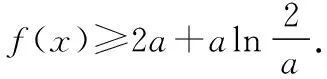
【策略1】隐零点换元.

(Ⅰ)略；

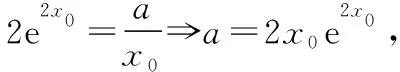
又∵a=2x0e2x0，即证:e2x0-2x0e2x0lnx0≥4x0e2x0-2x0e2x0(lnx0+2x0)，

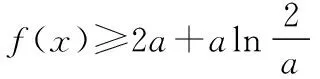
【策略2】视a为主元.

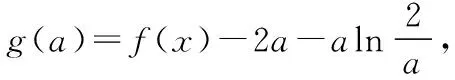
∴当x∈(0,2ex)时，g′(a)<0；当x∈(2ex,+∞)时，g′(a)>0，

即gmin(a)=g(2ex)=e2x-2exlnx-4ex+2exln(ex)=e2x-2ex，

然后求导，易证上式大于或等于0.

【评注】所证不等式与a相关的部分比较简单，采用视a为主元的策略，最后求导之后极值点也可以表示出来，降低了难度.

【策略3】放缩法.

利用ex≥ex可得f(x)≥2ex-alnx，

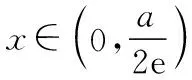
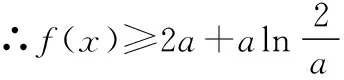
【评注】所给函数是含指、对数的混合式，考虑采用放缩法.

(Ⅰ)求a,b的值；

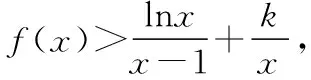
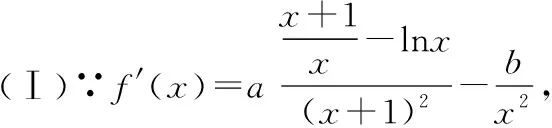
∴a=b=1.

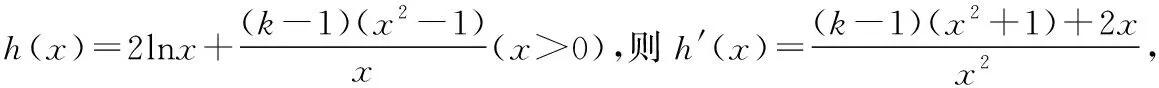
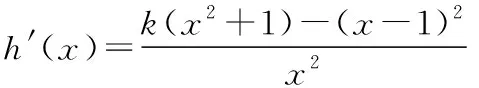
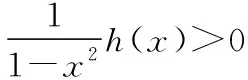
综上可得，k∈(-∞,0].

【评注】第(Ⅱ)问如果直接求导，相当麻烦.由于不等式含有lnx，于是采用“对数单身狗”来简化导函数.

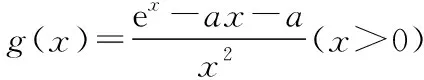
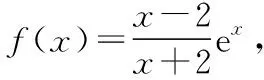
∵当x∈(-∞,-2)∪(-2,+∞)时，f′(x)>0，

∴f(x)在(-∞,-2)和(-2,+∞)上单调递增，

由(Ⅰ)知，f(x)+a单调递增，对任意的a∈[0,1)，f(0)+a=a-1<0，

f(2)+a=a≥0，因此，存在唯一xa∈(0,2]，使得f(xa)+a=0，即g′(xa)=0，

当0

当x>xa时，f(x)+a>0，g′(x)>0,g(x)单调递增.

因此g(x)在x=xa处取得最小值，最小值

【评注】该题第二问关键之处在于对g(x)求导之后的变型:除了转化为f(x)之外，还体现了“指数找基友”的策略.

(Ⅰ)讨论f(x)的单调性；

(ⅰ)若a≤2，则f′(x)≤0，当且仅当a=2，x=1时f′(x)=0，

所以f(x)在(0,+∞)上单调递减.

(Ⅱ)由(Ⅰ)知，当且仅当a>2时，f(x)存在两个极值点.

由于f(x)的两个极值点x1，x2满足x2-ax+1=0，所以x1x2=1，不妨设0

【评注】该题第(Ⅱ)问是隐零点的处理，这里利用韦达定理，找到两个极值点x1与x2的联系，再利用x1x2=1换元，变成单变量的恒成立问题.