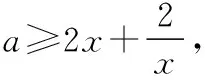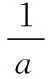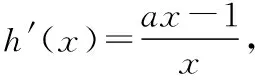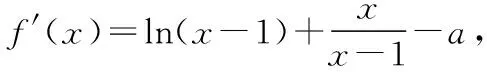摭谈含参导数题的分类讨论标准及优化策略
湖北 周 威
分类讨论思想是高中数学重要的思想方法,在对学生数学思维的考查方面有着独特的作用,因此是历年高考的必考点,特别是在导数综合题中分类讨论思想的应用,是我们不能回避的问题,例如2019年全国卷Ⅲ文、理科20题单调性讨论及根据最值求参数,2017年、2018年全国卷Ⅰ理科21题判断单调性,2017年全国卷Ⅱ理科21题求参数的范围等考题琳琅满目.既然是无法避免的问题,只有基于分类讨论思想在学习中做到合理、恰当分类以及掌握最常规的优化策略,才是备考的重点.通过分类讨论促进数学思维发展,形成规范化思考问题的品质,形成一丝不苟、严谨求实的科学精神.
一、单调性讨论的恰当分类标准
在高考导数综合题中单调性是必须要讨论的问题,因为单调性是解决后续问题的关键,而伴随单调性问题大多有参数的引入,由于参数取值不同导致结果的不同,因此给数学问题带来了不确定因素,从而就必须分类讨论.那么,如何才能在分类中做到恰当、合理呢?这就必须遵循恰当分类的基本原则,即根据一个相对统一的标准,做到不重不漏,这其实也就是分类讨论思想的核心.因为很多学生不知道这个标准如何确定,从而成为害怕、回避的主要原因.那么,单调性分类讨论时这个标准是什么呢?
1.准确找出界点
一般地,只要严格按照步骤先在一条数轴上标出各种界点(关于定义域的界点、导函数因式分解中不含参数的零点或导函数有无零点时的界点),然后遵循从左到右(或者从右到左)进行分段式讨论,最后再整合、归并就能做到恰当分类、不重不漏.
【例1】讨论函数f(x)=2ax-2lnx在区间(1,+∞)上的单调性.
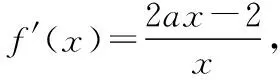
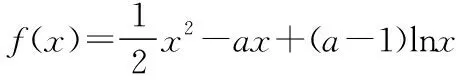

当a-1≤0时,即a≤1时,f(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
当0 当a-1=1时,即a=2时,f(x)在(0,+∞)上单调递增; 当a-1>1时,即a>2时,f(x)在(0,1),(a-1,+∞)上单调递增,在(1,a-1)上单调递减. 【评注】对f(x)>g(x)的处理,一般是构造函数h(x)=f(x)-g(x),然后进行求导, 一般情况下,含参函数求导后决定其符号的都是一次或二次函数模型,通过例1、例2让学生更加亲切、轻松地掌握含参函数单调性处理的一般方法,再通过相关界点分类讨论研究h(x)的单调性(极值、图象),从而解决问题. 2.借助二阶导数或判别式 对于无法通过因式分解确定零点作为界点的情形,如何进行恰当分类呢? 【例3】已知函数f(x)=ax+x2-xlna-a(a>0且a≠1),讨论f(x)的零点个数. 【例4】若a≥0,讨论函数f(x)=(1+ax2)ex-2的单调性. 【分析】函数的定义域为R,求导得f′(x)=(ax2+2ax+1)ex,因此需要考虑a=0,a>0两种情况. 当a=0时,f′(x)=ex>0,f(x)在R上单调递增; 当a>0时,ax2+2ax+1=0有可能有根,也可能无根,因此需继续分类: 当4a2-4a≤0时,即0 【评注】若f′(x)无法因式分解或无法确定正负时,需要通过题意中具体情况分类讨论,判断是否要继续对f′(x)进行求导得到f″(x),结合f′(x)、f″(x)一起判断f(x)的单调性或通过f′(x)=0的判别式分类讨论f(x)的单调性. 1.分离变量法 分离变量法一直是解决含参变量取值范围问题的常用方法,特别是含单变量的取值范围问题,分离变量能减少导数综合题中分类讨论层次. 【例5】已知函数f(x)=axex-x2-2x+1(其中a∈R,e为自然对数的底数).若x≥1时,f(x)≥0恒成立,求a的取值范围. 【评注】分离变量后构造h(x),其求导看似复杂,实则计算后恰好分子中不含ex,给计算带来了方便.对于单变量能分离的情形,甚至能达到避免分类讨论的目的. 【练习】已知函数f(x)=x2-ax+2lnx(a为常数),若f(x)是定义域上的单调函数,求a的取值范围. 综上,f(x)是定义域上的单调函数时a的取值范围是(-∞,4]. 2.利用局部单调性 怎样利用局部单调性质呢?主要根据函数零点及其导函数的正负.当函数f(x)满足f(x0)=0时,且在某区间内f(x)≥0(f(x)≤0)恒成立,则可结合f′(x0)的正负来确定参数的范围,然后验证在此范围内是否能得出题设中的已知结论.比如已知条件中有f(x)≥0,根据f(x0)=0,那么必有f′(x0)≥0,从而能得出关于参数的范围,然后根据这个范围,验证其能否得到f(x)≥0,如果能则参数范围即为所求. 【例6】(2017·全国卷Ⅱ理·21节选)已知函数f(x)=ax2-ax-xlnx,且f(x)≥0,求a. 【练习】已知函数f(x)=xln(x-1)-a(x-2)(a∈R),当x∈(2,+∞)时,f(x)>0恒成立,求a的取值范围. 《普通高中数学课程标准(2017年版)》在命题原则里强调,高考考查内容要注重数学本质、通性通法,淡化解题技巧.因此,我们不能一味的追寻如何规避分类讨论,寻求“偏、怪”的解题技巧,反而要熟悉、熟练分类讨论的标准、步骤等的“通性通法”.在专题复习或解题教学中,需要分类讨论的情形不尽相同,但其基本步骤可概括为先确定讨论的对象及范围,然后根据恰当分类,做到不重不漏,最后进行逐步讨论、归并和总结.同时,当分类讨论确实过于烦琐时,正所谓“正难则反”,一些减少、甚至规避分类讨论的优化策略,也是数学思维的一种体现,也应该掌握,开拓数学视野,提升核心素养.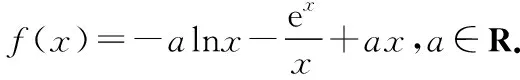
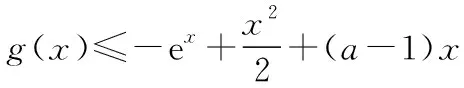


二、常规的优化策略