基本不等式模块复习要注意的几个问题

安徽 朱启州

基本不等式具有将“和式”与“积式”互化的放缩功能，应用广泛.在教学中要强化因式制宜，运用合理拆添项、配凑等恒等变形，创造基本不等式的应用条件.应用基本不等式的步骤可概括为“一正二定三相等”，需特别注意满足取等号的条件.与完全平方式等恒等式的应用一样，基本不等式应用只有达到精熟，才能当用时用、呼之即来.现就基本不等式模块复习教学谈谈自己的一点体会，供读者参考.

一、重视梳理基本不等式几种常见形式及其之间的关系

从上述恒成立的不等式可以看出，这些不等式的根源是(a-b)2≥0.理解掌握基本不等式的几种常见形式，是我们应用基本不等式正确解题的知识基础，应用时特别要注意每个不等式成立的条件.

二、不可忽视基本不等式的文化背景、几何意义

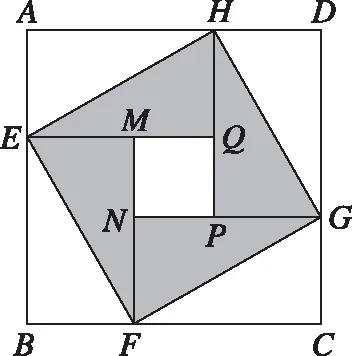
图1

图2

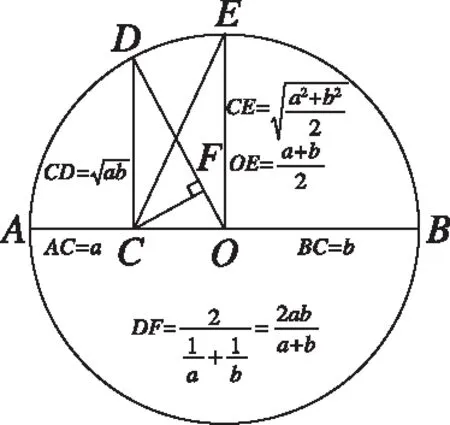
图3

三、理解函数、方程、基本不等式之间的本质联系，重视函数方法

基于此，在应用基本不等式求最值问题时，我们也会考虑利用函数方法.

【例1】在正项等比数列{an}中，a4+a3-a2-a1=5，则a5+a6的最小值为________.

【解析】设数列{an}的公比为q，则a1>0,q>0，

因为5=a4+a3-a2-a1=a1q3+a1q2-a1q-a1=a1(1+q)(q2-1)，

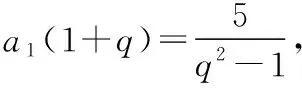
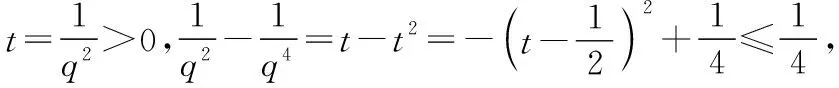
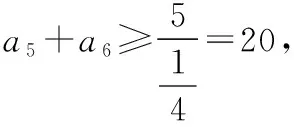
解法二：令q2=m，显然m>1，

所以a5+a6的最小值为20.

【说明】解法一就是以函数视角为出发点来解题的，解法二从应用基本不等式的角度来解题的，但共同点都需要对目标式进行合理的变形，从而实现转化.

这一模块复习的目的就是让学生掌握运用基本不等式求最值方法，掌握常见代数式变形方法，拓宽了求最值的思路.当然，本模块的复习目的是在函数、方程、不等式高度融合的基础上实现知识的成网成块，从而实现学生解题素养的提升.

四、通过对比体验认识应用基本不等式的必要性

既然利用函数模型可以代替基本不等式解决问题，为什么还要学习基本不等式呢？打个比方，正如我们在初中阶段学习了整式运算和乘法公式一样，正是因为应用基本不等式解决问题广泛与便利，所以学习和掌握基本不等式是很有必要的.下面举一例说明.

运用重要不等式，关键是要依据目标式的特点进行变形，以能运用重要不等式.

下面运用函数方法，就需要化二元代数式为一元代数式，从而转化为函数问题.

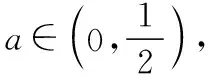
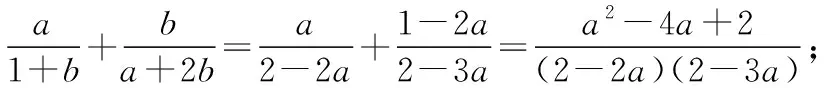
Δ=(4-10y)2-4(6y-1)(4y-2)=4y2-16y+8≥0，

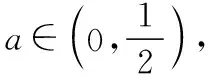
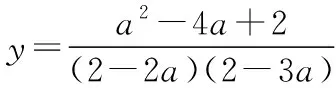
五、掌握应用基本不等式几个常见模式

1.由目标式特点凑成定值是运用基本不等式解题的关键

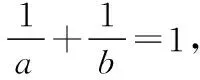
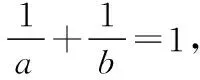
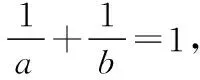
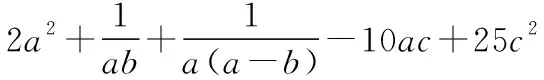
【解析】由a>b>c>0，

【说明】根据问题提供的条件，凑出和或积为定值往往是解题的关键，因此基于目标式的结构特征进行变形，凑出定值的变形就显得更为重要.

2.“一正二定三相等”，切实检查等号是否成立

【例5】下列命题:

【说明】“一正二定三相等”是应用基本不等式的重要步骤，要切实验证每一步骤成立的条件，不能敷衍了事.

3.常数代换是最常运用的模式

【解析】因为a+b=2，b>0，

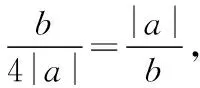
【说明】常数代换方法常见于条件代数式与目标代数式分别是整式与分式的情况，目的是实现目标代数式整式与分式等不同形式的转换，或凑出积式或和式为定值，从而为应用基本不等式创造条件，如2019年全国卷Ⅰ第23题.