不等式“恒成立”“存在成立”问题的破解策略

福建 吴志鹏 陈玉兰

不等式“恒成立”与“存在成立”问题是高考热点也是难点.它考查学生的化归与转化思想、逻辑推理和运算求解能力，要求学生具有扎实的数学基本功和较高的数学素养.不等式“恒成立”与“存在性”问题属于“全称量词与存在量词”的考查范畴，考纲要求并不复杂，但它涵盖的知识量大，试题的难易度能得到比较好的控制.既可作为基础题进行考查，有时也出现在选做题中；但它作为压轴题考查时，常表现为一题中既有若干研究对象即若干函数(常见2个)，有若干变量，又有“存在”或“任意”等量词的干扰，致使很大一部分的学生“望题生畏”，为了降低学生的解题难度，我们总结了以下破解策略.

一、排除干扰

弄清我们所要研究的对象，对于一些问题我们通过分离参数法、数形结合法、分类讨论法等获得以下两个模型(包含了恒成立与存在成立)：

1.x∈D,m≥f(x)(m≤f(x))成立.

变式：①x∈D,m≥f(x)±g(x)(m≤f(x)±g(x))成立；

②x∈D,m≥f(x)·g(x)(m≤f(x)·g(x))成立；

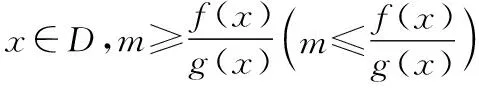
由于f(x),g(x)的变量是同一的，此时我们可将f(x),g(x)的关系式设为函数T(x)，这样就能减少所需研究函数的个数，有助于提高解题效率.

2.x1∈A,x2∈B,f(x1)≤g(x2)成立或x1,x2∈A,f(x1)-f(x2)<0成立;

由于函数的自变量不同一，x1,x2可以相同也可以相异，为此我们必须分别研究函数f(x)与g(x)或是研究函数f(x)的最大值或最小值两种情况.

研究对象的确定，主要是通过观察函数自变量是否同一，同一则大多数情况可转化为一个函数来研究，不同一则分成两个函数进行研究或是研究一个函数的两种情况.

二、转化确立

1.文字语言的转化，问题的呈现形式有：不等式的解集为R，不等式f(x)>0的解集为空集即f(x)≤0的解为全体实数；不等式在区间[a,b]上成立;不等式的解集包含[a,b]，以上几种说法通常可转化为不等式“恒成立”问题;不等式的解集不为空集；不等式有解;存在[a,b]，使得不等式成立等通常可转化不等式“存在成立” 问题 .

2.对于不等式“恒成立”和“存在成立”这两类问题，可转化为求函数的最值比较问题，并利用其结果解决相应的求参问题或不等关系的证明.利用不等式“恒成立”解决“存在成立”问题，用熟悉的知识解决不熟悉的内容，是进行这类转化的一种较好的方法.

①∀x∈D,m≥f(x)(m≤f(x))成立⟹x∈D,m≥f(x)max(m≤f(x)min).

②∃x∈D,m≥f(x)(m≤f(x))成立⟹x∈D,m≥f(x)min(m≤f(x)max).

学生对不等式“恒成立”问题比较熟悉，图形意识也比较强烈，这类问题部分学生能够很好地掌握，对比“恒成立”问题与“存在成立”问题，其实质只是对其最值的性质进行了变换，最大值与最小值的互换，这个特征也是不等式“恒成立”问题与“存在成立”问题最重要的区别，理解了其区别，转化也就能做到“水到渠成”.

通过研究不等式恒成立问题：

∀x1∈A,∀x2∈B,f(x1)≤g(x2)成立

⟹f(x)max≤g(x)min,f(x)的定义域是A,g(x)的定义域是B.

通过不等式“恒成立”研究获得“存在成立”问题的三个结论：

①∀x1∈A,∃x2∈B,f(x1)≤g(x2)成立

⟹f(x)max≤g(x)max,f(x)的定义域是A,g(x)的定义域是B.

②∃x1∈A,∀x2∈B,f(x1)≤g(x2)成立

⟹f(x)min≤g(x)min,f(x)的定义域是A,g(x)的定义域是B.

③∃x1∈A,∃x2∈B,f(x1)≤g(x2)成立

⟹f(x)min≤g(x)max,f(x)的定义域是A,g(x)的定义域是B.

三、函数研究

不等式“恒成立”“存在成立”问题转化后就成了函数最值的比较，而要求函数的最值，就需要对函数进行研究，可利用导数、单调性的定义、基本不等式或函数的图象等对其进行研究，以获得函数在定义域内的最值.

四、结论获取

通过比较函数的最值大小获得参数的取值范围或证明不等关系.

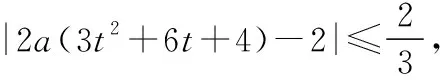
又3t2+6t+4=3(t+1)2+1≥1，

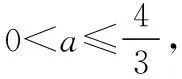
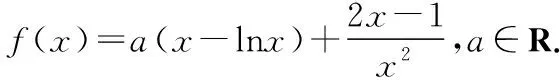
(Ⅰ)讨论f(x)的单调性；

则f(x)-f′(x)=g(x)+h(x)，

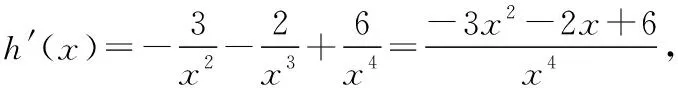
设φ(x)=-3x2-2x+6,则φ(x)在x∈[1,2]上单调递减，因为φ(1)=1,φ(2)=-10,

所以存在x0∈(1,2)，使得φ(x0)=0，且

当10,h(x)单调递增；

当x0

【例2】(2015·全国卷Ⅱ理·21)设函数f(x)=emx+x2-mx.

(Ⅰ)证明：f(x)在(-∞,0)上单调递减，在(0,+∞)上单调递增；

(Ⅱ)若对于任意x1,x2∈[-1,1]，都有|f(x1)-f(x2)|≤e-1，求m的取值范围.

解：(Ⅰ) 证明：略

(Ⅱ)由(Ⅰ)知,f(x)在(-∞,0)单调递减，在(0,+∞)单调递增，即f(x)在[-1,0]单调递减，在[0,1]单调递增，

所以f(x)在x=0处取得最小值.

当m=0时,f(x)=1+x2，此时f(x)在[-1,1]上的最大值为2，最小值为1,

所以此时|f(x1)-f(x2)|≤2-1≤e-1成立.

当m≠0时，f(-1)=e-m+1+m,f(1)=em+1-m,

令g(m)=f(1)-f(-1)=em-e-m-2m，由g′(m)=em+e-m-2≥0,

得g(m)在R上单调递增;

而g(0)=0，所以当m>0时，g(m)>0，即f(1)>f(-1),

所以当m<0时，g(m)<0，即f(1)

当m>0时，|f(x1)-f(x2)|≤f(1)-1=em-m≤e-1⟹0

当m<0时，|f(x1)-f(x2)|≤f(-1)-1=e-m+m≤e-1⟹-1≤m<0.

综上所得m的取值范围为[-1,1].

评析：本小题研究对象为函数f(x)，由于所给的自变量是不同一的，因此本题所研究的对象应视为函数f(x)的两种最值情况；对于任意x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤e-1成立，可转化为在区间[-1,1]上,|f(x1)-f(x2)|max≤e-1成立；研究函数f(x)在定义域内的最大值与最小值问题；最后利用不等关系进行比较获得m的范围.

g(x)在[1,2]上的最大值为max{g(1),g(2)}，所以有

解得m≥8-5ln2,

所以实数m的取值范围为[8-5ln2,+∞).

评析：本题研究对象为不同的两个函数f(x)和g(x)，且自变量也不是同一的，所以必须分别对两个函数进行研究，利用不等式成立的类型进行转化，即f(x)max≥g(x)max；在各自的定义域内利用导数或其他手段研究函数，寻求所需的最值；最后利用不等关系求得m的取值范围.

结语：不等式“恒成立”“存在成立”问题的破解策略：排除干扰，通过自变量是否同一确定函数是否可合一，以减少函数个数的研究；再将不等式“恒成立”“存在成立”两类不同情况转化为求函数的某类最值问题，以“恒成立”为蓝本进行“存在成立”的转化；利用所学知识对函数的图象或性质进行研究，以获得所需的最值；比较最值获得参数的范围或证得结论.突破以上几个关键的解题环节，破解不等式“恒成立”“存在成立”问题就将变得“轻而易举”，其内容将不再是学生学习的难点.