十年全国卷压轴题中的函数与方程思想研究综述

陕西 刘再平

一、函数与方程思想的内涵、原则与思维模式

1、函数与方程思想的内涵

函数是刻画现实世界中运动变化规律的一类重要模型，是高中数学的核心模块，贯穿高中数学课程的始终. 函数思想是基于对函数概念的本质认识，用联系与变化的观点提出数学对象、抽象数量特征并建立函数关系，用函数的知识来观察、分析和解决问题的一种思维方式.方程思想是基于对方程概念的本质认识，根据问题所表征的意思设一些未知量，然后根据题设中各个量之间的联系，建立变量之间的等量关系，即列出方程或方程组去分析和转化问题，使得问题获得解决的一种思维方式.

函数与方程联系紧密，可以互相转化. 若一个函数有解析式，那么这个解析式就可以看成一个方程，反过来一个二元方程中，两个非空数集变量间存在着某种映射关系，则这个方程就可以看成一个函数.如：解方程f(x)=0可以转化为求函数y=f(x)的零点;方程f(x)=a有解可以转化为参数a属于函数y=f(x)的值域;方程f(x)=g(x)的解可以转化为两函数y=f(x)与y=g(x)的交点问题或转化为新函数y=f(x)-g(x)的零点个数问题.

2、函数与方程思想的原则

在运用函数与方程思想时，需要遵循以下原则：

(1) 转化等价性原则. 函数与方程问题互相转化的前提是要保证转化的等价性，如：在涉及三角换元的转化过程中要注意三角函数的有界性，从而避免扩大了函数的定义域.

(2) 简单性原则. 数学解题中，频繁的复杂推理和运算会让人的数学学习兴趣受到消耗，所以要善于对比和辨析，在可接受的范围内追求其解法的简单性. 如：2012年全国卷文科函数与导数压轴题可以通过变参分离，转化为函数与方程问题，再通过隐含零点的代换解决，显然这样解决比较烦琐，直接运用不等式与函数的最值解决更为简洁.

3、运用函数与方程思想解题的思维程序

评注：(1)函数与方程是高中数学学习的主线，函数与方程思想也是中学阶段运用最频繁的数学思想，在解决相关问题时要有运用函数与方程转化的意识；

(2)函数与方程的引入方法有很多，特别是函数的引入手段非常丰富，如: 整体引入、局部引入、参变分离引入、分离函数引入、作差引入等；

(3)在解决引入的函数与方程问题时，通常会用到函数的单调性、奇偶性、周期性、函数最值或函数的图象等.

二、近十年全国卷压轴题中的函数与方程思想统计与分析

近十年全国卷共42套试卷，即有42道压轴题，其中35道是函数与导数压轴题，约占总量的83.3%，这也表明函数与导数问题承担了大部分全国卷压轴题的角色，所以下面主要研究近十年全国卷函数与导数压轴题中的函数与方程思想，具体如下统计：

从上表可以获得以下结论：

首先，近十年全国卷35道函数与导数压轴题有32道是对函数与方程思想的考查，约占91.4%，说明函数与方程思想在全国卷函数与导数压轴题中考查得十分频繁，不容忽视.

其次，从上述表格不难发现，函数与方程思想在2010年-2018年的函数与导数压轴题中考查较多，然而在2019年高考压轴题中出现较少，这是因为2019年全国卷Ⅰ、Ⅱ、Ⅲ的六套数学试卷的压轴题有五道变为了圆锥曲线试题，然而这并不能断定2020年高考全国卷不会以函数与导数的内容命制压轴题，更不能说明高考会降低对函数与方程思想的考查.

最后，近十年文理科全国卷函数与导数压轴题对函数与方程思想的考查频率一样高，这说明函数与方程思想要引起文理科师生的共同重视，具体来说，要重视构造函数和通过参变分离将方程问题转化为函数交点问题的能力.

三、十年压轴题中的函数与方程的引入方法

如何引入函数和方程呢？引入函数和方程的具体方法有哪些呢？下面将以近十年函数与导数压轴题为例进行阐述，鉴于篇幅，下文只分析函数与方程的引入思路，不给出详细的解答过程.

1、通过函数零点与方程的转化引入

由于函数的零点就是函数解析式等于零的方程的根，也是函数与x轴交点的横坐标，可以通过分离函数转化为两函数交点问题，所以通过零点与方程的转化是常见的引入方式.

例1(2018·全国卷Ⅱ理·21)已知函数f(x)=

ex-ax2.

(Ⅰ)若a=1，证明：当x≥0时，f(x)≥1；

(Ⅱ)若f(x)在(0,+∞)只有一个零点，求a.

运用思路：(Ⅰ)证明略.

(Ⅱ)由题函数f(x)在(0,+∞)只有一个零点，即方程f(x)=0在(0,+∞)只有一个根，通过代数变形后则方程1-ax2e-x=0在(0,+∞)只有一个根，所以引入函数g(x)=1-ax2e-x，问题转化为函数g(x)在(0,+∞)上与x轴只有一个交点.

2、通过隐含零点与方程的转化引入

函数的隐含零点与方程的转化是全国卷函数与导数压轴题中的重点、热点与难点，主要是要运用零点存在性定理准确的找到隐含的零点，再将其转化为方程问题，从而实现有效的代数变换，如：2019年全国卷Ⅱ文科压轴题、2017年全国卷Ⅱ理科压轴题、2016年全国卷Ⅱ理科压轴题等.

例2(2015·全国卷Ⅰ文·21)设函数f(x)=e2x-alnx.

(Ⅰ)讨论f(x)的导函数f′(x)零点的个数；

运用思路：(Ⅰ)当a≤0时，f′(x)没有零点；当a>0时，f′(x)存在唯一零点;

3、通过函数极值与方程的转化引入

函数极值问题也是全国卷高考常见的压轴题，由于函数极值点处的导数值必然为零，所以函数极值问题常常转化为方程根的问题，运用函数与方程思想解决.

(Ⅰ)讨论f(x)的单调性；

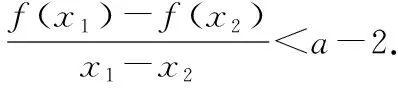
(Ⅱ)由题f(x)存在两个极值点x1,x2，因为极值点处的导数值为零，所以函数极值问题可以转化：方程f′(x)=0存在两个根x1,x2，通过代数变形知方程x2-ax+1=0存在两个根x1,x2，再结合一元二次方程的韦达定理等知识解决问题.

4、通过不等式与函数的转化引入

函数与不等式综合问题是近十年全国卷中出现频率最高的压轴题类型，函数与不等式压轴题通常可以结合函数思想，将不等式问题转化为函数问题.

例4(2016·全国卷Ⅲ文·21)设函数f(x)=lnx-x+1.

(Ⅰ)讨论f(x)的单调性；

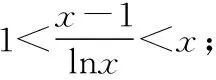
(Ⅲ)设c>1，证明当x∈(0,1)时，1+(c-1)x>cx.

运用思路：(Ⅰ)当01时，f(x)单调递减；

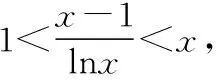
(Ⅲ)由题要证1+(c-1)x>cx，即证cx-1-(c-1)x<0，引入函数m(x)=cx-(c-1)x-1，x∈(0,1)，即转为证明函数m(x)<0.

5、通过绝对值与函数最值的转化引入

例5(2015·全国卷Ⅱ理·21)设函数f(x)=emx+x2-mx.

(Ⅰ)证明：f(x)在(-∞,0)上单调递减，在(0,+∞)上单调递增；

(Ⅱ)若对于任意x1,x2∈[-1,1]，都有|f(x1)-f(x2)|≤e-1，求m的取值范围.

运用思路：(Ⅰ)证明略；

(Ⅱ)由题对于任意x1,x2∈[-1,1]，都有|f(x1)-f(x2)|≤e-1，可以将绝对值问题转化为函数最值问题：对于任意x∈[-1,1]，都有f(x)max-f(x)min≤e-1.

四、教学建议

在函数与导数问题的教学中,函数与方程思想是师生不得不重视的数学思想方法，当然同一道函数与导数问题解决方法不同，其函数与方程的引入视角也有区别,这需要师生的辨析与优化.那么，在函数与导数压轴题的教学中如何渗透函数与方程思想呢？笔者建议如下：

(1)充分挖掘教材上的函数与方程思想. 如教材在探究函数的零点时，将函数y=f(x)的零点定义为方程f(x)=0的根，反过来方程f(x)=0的根也可以视为函数y=f(x)的零点等，这些教材核心内容都是培养学生函数与方程思想的好素材.

(2)教师要上好数学概念课以及章末复习课，因为数学概念的生成往往渗透着数学思想，章末复习课不仅仅是组织学生做大量的习题，而是要突出章末复习课的两个核心功能：一是构建本章节知识的思维联系，二是渗透数学思想方法.

(3)有目的有意识的渗透、介绍和突出与函数导数压轴题有关的函数与方程思想，展示函数与方程思想在指导数学解题方面的魅力，再通过讲练结合、合作探究与归纳领悟等多种方式促进学生感悟函数与方程思想，提高学生灵活运用函数与方程思想解决函数与导数压轴题的能力.

(4)有计划、有步骤循序渐进的渗透函数与方程思想. 由于数学思想方法教学具有隐晦性、活动性、主观性和差异性，所以数学思想方法的教学一般都不是一蹴而就、一气呵成的，它需要教师长期的渗透，学生慢慢的感悟和运用，这将是一个静等花开的过程.