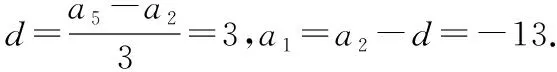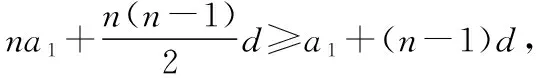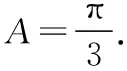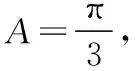追根溯源 遇新不惊——高考新题型剖析

山东 张邦杰

今年全国高考模拟试卷第17题首次出现开放型试题，形式新颖，很好地考查了学生对知识掌握的熟练程度和分析问题的能力.所谓开放型试题是指条件不确定或者答案不唯一，具有多种不同的解法、情景新颖，有别于传统的试题.一般试卷中出现的传统试题都是已知条件比较充分，研究的结论也是确定的问题，而开放型的题目条件可能不确定，其结论也可能具有不确定性.开放型题目的背景新颖、立意深刻，能起到“举一反三”的效果，这是对传统的“题海战术”的极大挑战.《普通高中数学课程标准(2017年版)》在内容标准部分强调数学探究的教育价值，并且贯穿于整个高中数学课程的重要内容，而开放型试题不仅考查了学生的数学探究能力和数学素养水平，同时也对高中课程教学由关注教到关注学的转变起到一定的推动作用.结果显示学生在遇到这一类问题时，解答效果并不理想，失分现象严重，为加强对高考开放型试题的分析研究，帮助学生答疑解惑，现对典型的开放型试题进行分类剖析.

题型剖析：(2020·全国统一考试模拟卷·17)在①b1+b3=a2,②a4=b4,③S5=-25这三个条件中任选一个，补充在下面问题中，若问题中的k存在，求k的值;若k不存在，说明理由.

设等差数列{an}的前n项和为Sn,{bn}是等比数列，________，b1=a5,b2=3,b5=-81,是否存在k,使得Sk>Sk+1且Sk+1

注:如果选择多个条件分别解答，按第一个解答计分.

【解题策略】本题中条件不完整，给出三个条件添加选择项，构建出完整题目后再解决问题，因此需要对题干要进行整体详细分析，找出条件和结论的内在联系是解题关键，最后再决定选哪个条件是自己比较容易把握和入手的.根据条件中{bn}是等比数列，由b2,b5易确定{bn}，从而确定a5，那么三个条件无论选择哪一个都可确定{an}.再分析使Sk>Sk+1,Sk+1

【详细解析】在等比数列{bn}中，b2=3,b5=-81,因为b5=b2·q3，所以其公比q=-3,

所以bn=b2(-3)n-2=3×(-3)n-2,从而a5=b1=-1.

若存在k,使得Sk>Sk+1,即Sk>Sk+ak+1,从而ak+1<0;

同理，若使得Sk+10.

(方法一)若选①：由b1+b3=a2,得a2=-1-9=-10,所以an=3n-16,当k=4时，满足a5<0,且a6>0成立;

若选②：由a4=b4=27,且a5=-1,所以等差数列{an}为递减数列，故不存在ak+1<0且ak+2>0;

若选②或选③(仿上可解决，过程略).

【解题反思】从本题的解析中可以看出这种开放型试题的解答是多样性的，更能考查出学生的数学素养水平，但对知识本质的考查我们并不陌生，只要熟练得掌握所考查知识，理解透彻，给出完美的解答并不困难.因为往年高考试题中并没有这种形式的开放型试题，下面就在剖析2019年全国卷试题的基础上，探究新题型的应答.

问题研究一:(2019·全国卷Ⅰ文·18)记Sn为等差数列{an}的前n项和.已知S9=-a5.

(Ⅰ)若a3=4，求{an}的通项公式；

(Ⅱ)若a1>0，求使得Sn≥an的n的取值范围.

【解题策略】(Ⅰ)条件中给出了a3=4，S9=-a5．直接设出等差数列的首项和公差，易建立关于a1和d的方程组，求得a1和d的值，从而求出{an}的通项公式；

(Ⅱ)由S9=-a5得a5=0，又a1>0，可知d<0，将Sn≥an，转化为a1和d的形式，得到关于n的不等式，从而求得结果.

所以等差数列{an}的通项公式为an=-2n+10.

(Ⅱ)由条件S9=-a5，得9a5=-a5，即a5=0，

因为a1>0，所以d<0，并且有a5=a1+4d=0，所以有a1=-4d.

因为d<0，所以n2-9n≤2n-10，即n2-11n+10≤0，

解得1≤n≤10，所以n的取值范围是1≤n≤10(n∈N*).

【解题反思】本题考查的是等差数列的通项公式和等差数列的求和公式，在解题的过程中，需要认真分析题意，重视对数列基本量的分析并能正确求解不等式，熟练掌握基础知识是正确解题的关键.下面将该题改编成一道开放型试题，从而体会新题型与传统题型考查的异同点.

题型探析：在①S9=-a5,②S7=S2,③当n=4或n=5时，Sn均取最大值,这三个条件中任选一个，补充在下面问题中，若问题中的n存在，请求出n的值；若不存在，请说明理由.

记Sn为等差数列{an}的前n项和，a1>0，若________，是否存在n使得Sn≥an？

注：如果选择多个条件分别解答，按第一个解答计分.

【解题策略】本题给出的三个供选择的条件都涉及了等差数列{an}的前n项和Sn，那么an与Sn之间的联系及性质将是本题考查的关键知识点.

②由S7=S2，知S7-S2=a3+a4+a5+a6+a7=5a5=0，所以a5=0；

③由n=4或n=5时，Sn均取最大值，且a1>0，易知等差数列{an}单调递减，S4=S5，所以a5=0.

【详细解析】请参考本题解题策略及2019年全国卷Ⅰ文科第18题第(Ⅱ)问的解答过程，此处略.

【解题反思】由此题的设计可见，虽然题目的呈现方式有所变化，但与原高考题所考查的知识方面差别不大，所以对知识的学习要关注知识的本质及知识间的内在联系，重视对问题的探究，不搞“题海战术”，就能做到以不变应万变，追根溯源，遇新不惊，得到完美的解答.全国高考模拟试卷中的开放题在第一道解答题位置上，此处往往考查数列或三角函数及三角恒等换、解三角形等知识，下面针对三角函数这个板块探究一下本题型.

问题研究二:(2019·全国卷Ⅰ理·17)△ABC的内角A，B，C的对边分别为a，b，c.设(sinB-sinC)2=sin2A-sinBsinC.

(Ⅰ)求A；

即sin2B+sin2C-sin2A=sinBsinC,

由正弦定理可得b2+c2-a2=bc,

(Ⅱ)本文不探讨此问题，解析略.

【解题反思】本题考查利用正弦定理、余弦定理解三角形的问题，同时涉及两角和差正弦公式、同角三角函数关系的应用，解题关键是能够利用正弦定理对边角关系式进行化简，得到余弦定理的形式或角之间的关系.下面对这道高考题改编成一道开放型试题，从而思考与原高考题考查知识及能力方面的异同点.

若问题中的C存在，请求出C的值;若不存在，请说明理由.

注：若选择多个条件分别解答，按第一个解答计分.

【解题策略】本题给出的三个供选择的条件都可以通过正弦定理或余弦定理进行转化，从而求出A的值，然后再对问题进行解决.

【详细解析】(Ⅰ)△ABC的内角A，B，C的对边分别为a，b，c,

即sin2B+sin2C-sin2A=sinBsinC,

由正弦定理可得b2+c2-a2=bc,

∴2 sinBcosA=sinAcosC+sinCcosA, ∴2 sinB· cosA=sin(A+C)= sinB，

下面的解答过程请参考选择①的解答过程，不再重述.

【解题反思】本题所提供的三个添加条件无论选择哪一个，所考查的知识与技能都与2019年全国卷Ⅰ理科17题相似，解题的关键都是对正弦正理和两角和与差公式的熟练应用，但在考查数学核心素养方面，新题型有较好的区分度.如果将本题中“是否存在C使得f(C)存在最大值？”改为“是否存在C使得f(C)存在最小值？”也是利用类似方法求解，在此不再赘述.

从以上两个知识板块的分析来看，新高考题型虽然在问题呈现方式上与往年高考题有所不同，更具有开放性和多样性，但只要我们在研究高考试题时能多思考和总结所考查知识的本质内涵及重视知识间的内在联系，对问题分析透彻，我们就能做到从容应答.这种题目形式的出现也体现了新高考趋势和《高中数学课程标准(2017年版)》的要求，希望在平常的数学教学中，能抛开“题海战术”，重视数学核心素养的提升，就可以以不变应万变，做到遇新不惊！