用数形结合思想求解2019年高考全国卷Ⅱ函数解答题

甘肃 吴天斌

函数解答题往往是高考数学试卷中难度最大的，它不仅运算量大，更突出的是立意新颖，构思精巧，思维容量大，大多数考生想不到、找不到解题的切入点与突破口，而心生畏惧，一筹莫展；数形结合思想往往是解决该类问题的有力杠杆与指路明灯，下面以2019年高考全国卷Ⅱ理科函数解答题为例，例析由数想形、以形助数、由形化数、数形兼备求解函数零点等相关问题中的应用，希望引起更多读者对数形结合思想的重视与深研.

(Ⅰ)讨论f(x)的单调性，并证明f(x)有且仅有两个零点；

(Ⅱ)设x0是f(x)的一个零点，证明曲线y=lnx在点A(x0,lnx0)处的切线也是曲线y=ex的切线.

分析：(Ⅰ)思路①(直接判断法)：先对函数f(x)求导，结合定义域，判断函数的单调性，画出函数f(x)图象草图，取一些特殊函数值，然后结合零点存在定理证明函数f(x)有且仅有两个零点；

思路②(极限、极值、最值分析法)：先对函数f(x)求导，结合定义域，判断函数的单调性，画出函数f(x)图象草图，求端点极限值或极值或最值，比较它们与0的大小关系，再结合零点存在定理证明函数f(x)有且仅有两个零点；

思路③(函数分离法)：先对函数f(x)求导，结合定义域，判断函数的单调性，然后令f(x)=0，将所给函数分离成两个熟悉的函数，两个新函数的交点个数即为原函数的零点个数.

(Ⅱ)思路①：先求出曲线y=lnx在点A(x0,lnx0)处的切线l，然后求出当曲线y=ex的切线l′的斜率与l的斜率相等时，再证明曲线y=ex的切线l′在纵轴上的截距与l在纵轴的截距相等即可；

解析：(Ⅰ)解法1：

解法2：

函数f(x)的单调性及草图同解法1所示；

①x∈(0,1),当x→0-时y→-∞，而x→1-时y→+∞，由f(x)单调性和零点存在定理知当x∈(0,1)，函数f(x)有唯一的零点；

②x∈(1,+∞)，当x→1+时y→-∞，当x→+∞时y→+∞，由f(x)单调性和零点存在定理知当x∈(1,+∞)，函数f(x)有唯一的零点；所以函数f(x)在定义域(0,1)∪(1,+∞)内有且仅有两个零点；

点评：x→0+指的是变量x从0的右侧趋向于0，x→1+指的是变量x从1的右侧趋向于1，其余类似，这种做法是把解法1推向于极限情形，更直接地解决问题，只不过对考生的知识、能力要求更高.

解法3：

函数f(x)的单调性同解法1，草图如图所示；

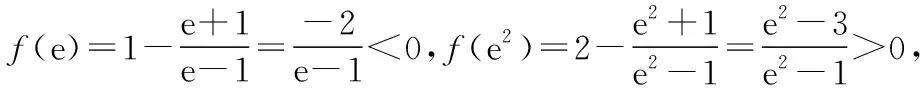
解法4：

函数f(x)的单调性同解法1；

点评：数形结合思想的本质是转化，由函数零点转化为两个我们最为熟悉的函数图象的交点，把复杂问题转化为较容易的问题，是数形结合思想的灵魂和精神所在；有时候，一个图形胜过千言万语，把数学的简洁美、直观美、形象美体现得淋漓尽致，这不但能起到简化运算，降低试题难度的作用，而且还能激发学生学习数学的兴趣.

(Ⅱ)解法1：

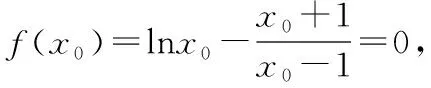
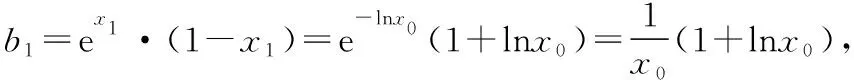
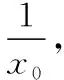
解法2：

在面对“山重水复疑无路”的解题困境时，数形结合思想往往是“柳暗花明又一村”的有效途径，所以我们要一边演算、一边思考、一边修正草图，画出与之匹配的图形，通过数与形的结合，将抽象问题具体化、复杂问题简单化、陌生问题熟悉化，这不仅有利于学生快速地找到解决问题的切入点、突破点，摸索解题思路，弄清问题实质，而且有助于减轻学生对函数解答题的恐惧心理，指引学生顺利求解，成功登顶.