一次函数中分类讨论思想的应用

葛 松

(江苏省泗阳实验初中开发区校区 223700)

一、遇到有坐标轴名称不明确时需要讨论

例1已知正比例函数y=k1x和一次函数y=k2x+b的图象都经过点P(-2，1)，且一次函数y=k2x+b的图象与y轴交点坐标是A(0，3)，求直线y=k1x和直线y=k2x+b与坐标轴围成的三角形的面积.

解如图1，∵直线y=k1x经过点P(-2，1)，

∵直线y=k2x+b经过点P(-2，1)和A(0，3),

∴一次函数的解析式为y=x+3.

(1)两条直线与y轴围成的△AOP的面积(如图).

(2)两条直线与x轴围成的△BOP的面积.

归纳由已知条件可以求出正比例函数和一次函数的解析式，但求两条直线与坐标轴围成的三角形的面积，并没有指明是与x轴围成的三角形的面积，还是与y轴围成的三角形的面积，致使需要进行分类讨论.

二、遇到有点的位置不明确时需要讨论

例2在平面直角坐标中，已知点A(-3，0)，B(2，6)，在x轴上有一点C，满足S△ABC=12，试求点C的坐标.

解如图2,过点B作BD⊥x轴，垂足为D.

∵S△ABC=12，∴AC=4.

(1)当点C在点A的右侧时，则点C坐标为(1，0);

(2)当点C在点A的左侧时，则点C坐标为(-7，0).

综上所述，点C的坐标为(1，0)或(-7，0).

归纳因在x轴上存在一点C位置的不确定，致使需要进行分类讨论，点C可以在点A的左侧，也可以在点A的右侧，这样的点C有两个.

三、遇到有两个量大小不明确时需要讨论

例3已知一次函数y=x+3的图象与x轴，y轴分别交于A、B两点.直线l经过原点，与直线AB交于C点；直线l把△AOB的面积分成2∶1两部分，试求直线l的解析式.

解如图3，过点C作CM⊥OA，垂足为M.

∵A(-3，0)，B(0，3) ∴S△AOB=4.5.

(1)若S△AOC∶S△BOC=2∶1，则S△AOC=3，即CM=2，求出点C坐标为(-1，2)，

∴直线l的解析式为y=-2x.

(2)若S△BOC∶S△AOC=2∶1，则S△AOC=1.5,

即CM=1，求出点C的坐标为(-2，1)，

∴直线l的解析式为y=-0.5x.

综上所述，直线l的解析式为y=-2x或y=-0.5x.

归纳因S△AOC和S△BOC的大小不明确，可能是S△AOC∶S△BOC=2∶1，也可能是S△BOC∶S△AOC=2∶1，所以需要进行分类讨论.

四、遇到有相等线段位置不确定时需要讨论

∴A(-3，0)，B(0，4)，∴OA=3，OB=4.

(1)当点A为顶点时，此时有AB=AC,如图4(2).

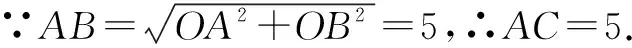
①若点C在A点的右侧时，则点C的坐标是C(2，0),

②若点C在A点的左侧时，则点C的坐标是C(-8，0).

(2)当点B为顶点时，此时有BA=BC,如图4(3),

则点C的坐标是(3，0).

(3)当点C为顶点时，此时有CA=CB,如图4(4).

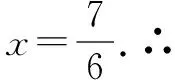
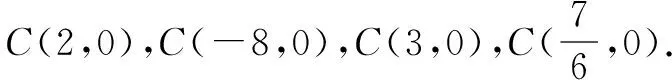
归纳要使△ABC为等腰三角形，因没有指明哪一个点为顶点(或哪一条边为底边)，所以要分(1)点A为顶点；(2)点B为顶点；(3)点C为顶点三种情况进行逐一分类讨论.

五、遇到有k或b的符号不确定时需要讨论

例5一次函数y=kx+b的图象与x轴、y轴分别交于A、B两点，且S△AOB=4，OA∶OB=1∶2，试求一次函数的解析式.

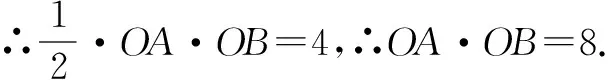
∵OA∶OB=1∶2，

∴设OA=x，OB=2x(x>0)，则x·2x=8，即x=2(-2舍去),

∴OA=2，OB=4.

(1)当k>0，b>0时，一次函数y=kx+b的图象过一、二、三象限，此时A(-2，0)，B(0，4).则一次函数的解析式为y=2x+4.

(2)当k>0，b<0时，一次函数y=kx+4的图象经过一、三、四象限，则一次函数的解析式为y=2x-4.

(3)当k<0，b>0时，一次函数y=kx+4的图象经过一、二、四象限，则一次函数的解析式为y=-2x+4.

(4)当k<0，b<0时，一次函数y=kx+b的图象经过二、三、四象限，则一次函数的解析式为y=-2x-4.

综上所述，一次函数解析式为y=2x±4或y=-2x±4.

归纳由S△AOB=4，OA∶OB=1∶2，可以求出OA和OB的长度，但由于k和b的符号不确定，k和b的值存在多种可能，所以需要分四种情况进行讨论.

六、遇到有增减性不明确时需要讨论

例6已知一次函数y=kx+b的自变量x的取值范围是-2≤x≤6，相应的函数值y的取值范围是-11≤y≤9，试求一次函数的解析式.

解(1)若函数y=kx+b为增函数,则一次函数y=kx+b图象的两个端点坐标分别是(-2，-11)和(6，9),即一次函数的解析式为y=2.5x-6.

(2)若函数y=kx+b为减函数，则函数y=kx+b图象的两个端点坐标分别是(-2，9)和(6，-11)，即一次函数的解析式为y=-2.5x+4.

综上所述，一次函数的解析式是y=2.5x-6或y=-2.5x+4.

归纳由于一次函数y=kx+b中的k值符号未明确，因此函数的增减性也不确定，与之相对应的两个端点的坐标同样也不确定，所以需要进行分类讨论.

总之，分类讨论思想是研究数学极为重要的一种数学思想和解题方法.在解题中，重在考查思考数学问题的逻辑性、周密性和全面性，力求做到正确、合理和严谨的分类.