初探翻折与隐圆

朱铭华

(江苏省苏州工业园区星湾学校 215021)

叶圣陶先生在《创造的儿童教育》中说；“处处是创造之地、天天是创造之时、人人是创造之人.”，是的，在我们的生活中处处有数学的素材等着我们去创造.

折纸，是我们日常生活中喜闻乐见的一种游戏，其实它就是非常贴近生活的数学素材， “折纸型”问题在近年屡屡出现在中考试题、综合实践活动中.因为在折叠纸张时，会出现许多几何概念，如：直线、角；角平分线、高；三角形、正方形、矩形；线和线的位置关系等等几何基本元素，还会有图形间的几何变换，如：对称、旋转、平移等.所以由折纸派生出来的平面图形的折叠问题能较全面的考查学生的动手操作能力、空间想象能力和数学建模能力，而在教学过程中学生在动手与动脑之间的数学学习中产生浓厚的探索、学习的兴趣.这种蕴含着丰富的数学思想的数学活动，在强调塑造数学能力的课程改革中也日益凸显其重要性.

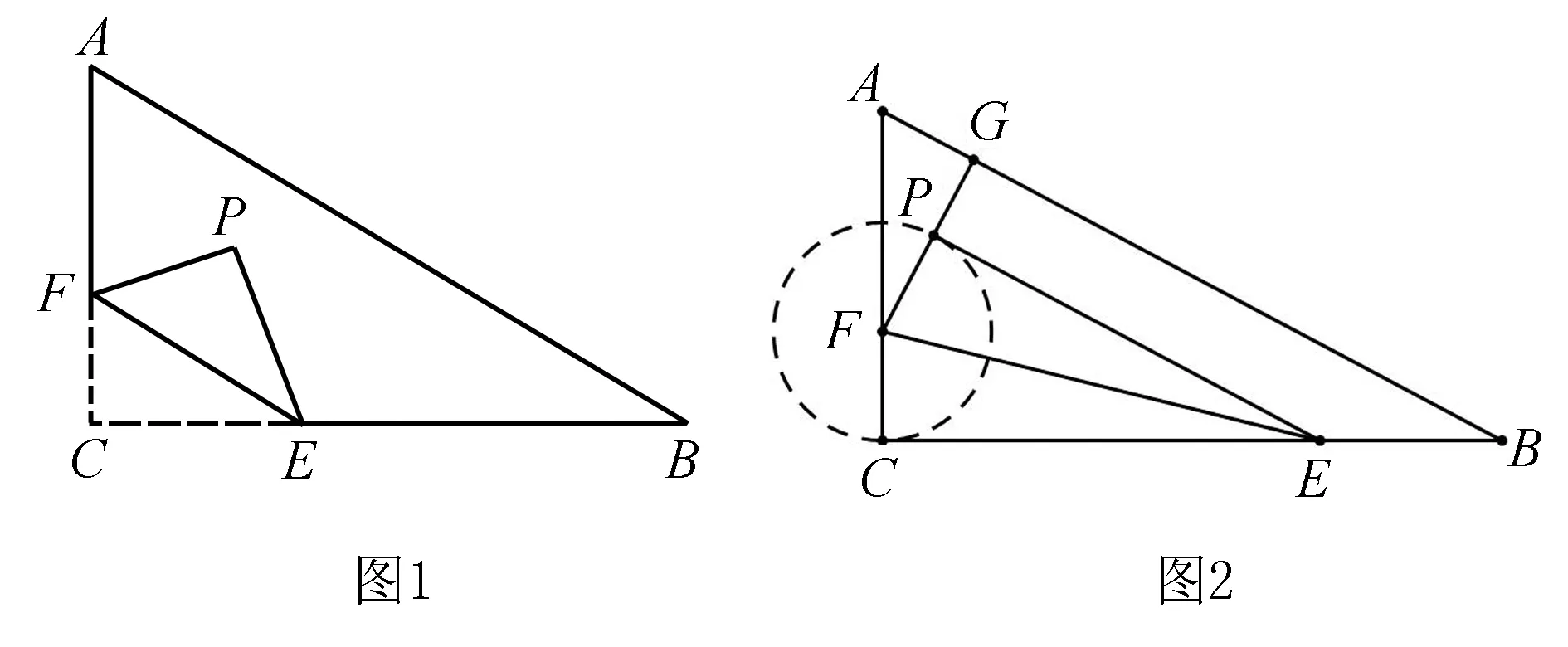
例题如图,在Rt△ABC中,∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是____.

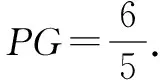
变式如图，已知矩形ΑΒCD中，ΑΒ=4，ΑD=m．动点Ρ从点D出发，在边DΑ上以每秒1个单位的速度向点Α运动，连接CΡ，作点D关于直线ΡC的对称点Ε．设点Ρ的运动时间为t(s)．

(1)若m=6，求当Ρ、Ε、Β三点在同一直线上时对应的t的值；

(2)当D、Ε、Β三点在同一直线上时，求m关于t的函数关系；

(3)已知m满足：在动点Ρ从点D到点Α的整个运动过程中，有且只有一个时刻t，使点Ε到直线ΒC的距离等于3，求所有这样的m的取值范围．

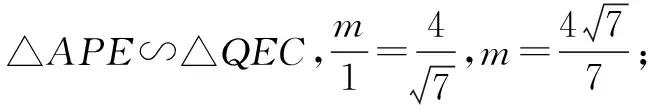
学以致用(来源：苏州工业园区九上数学期末考试28)如图，在矩形纸片ABCD中，AB=4，BC=5，点E在AD边上，EF⊥BC，垂足为F，点M在AB边上，BM=1，沿过点M的直线折叠该纸片，使点A落在线段EF上的点A'处，折痕为MN，点N在AD边上.

(1)画出折痕MN；(尺规作图，保留作图痕迹，不写画法)

(2)当BF=1.8 时，求折痕MN的长；

(3)写出折痕MN的条数与对应的BF的长度之间的关系.

分析(1)略.(2)由A′M=3,MH=1.8可知A′H=2.4,所以A′E=0.6.

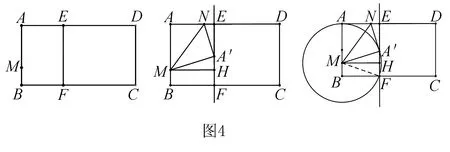
三、总结与反思

在这一系列的问题中，通过一个基本元素——折纸，让学生感受到：在生活中将周围事物与数学知识加以结合，处处都有数学，考虑问题时可以从数学的角度出发.陶行知认为：“活的人才教育不是灌输知识,……”.陶行知所说的“活的人才教育”，是指放手让学生“自主学习”，学生在自主学习过程中掌握了科学的方法，培养“自动力”，培养敢于创新的“自动”精神.也只有积极探索、认真研究和及时总结，才能更加深入的研究“折纸”中的奥妙.当然，折纸本身也不是数学的终点，它不能完全取代对所有数学活动的分析，数学是一种多边的人类活动，数学中的游戏娱乐、美学欣赏、哲学思考、实用价值探索等因素是如此紧密地交织在一起.