让学生有机会好好想问题——《积相等（一）》教学设计

章伟华

数学教育的核心是思维教育，培养学生的思维能力是数学教育最为重要的任务，教学中要重视设计挑战的、开放的数学任务，让学生有机会好好地想问题。本课教学涉及两个相关联的内容：一个是等量代换，另一个是等式的基本性质。等量代换是指一个量用与它相等的量去代替，它是数学中一种基本的思想方法，也是代数思想方法的基础。等式的基本性质其实是系统学习方程的开始，其核心思想是构建等量关系的数学模型。本节课的学习，是学生在观察天平的基础上，掌握等式的基本性质，引导学生通过比较发现规律，并能够用自己的语言清晰地表达出规律，为今后运用等式的基本性质解方程打基础，学生的推理归纳能力和清晰的语言表达能力是本课的重点。

【教学过程】

一、引入

师：天平有什么共同的特点？生：左右相等。

二、新授

（出示第一个天平）

师：你看到了什么？你能用一个等式来表示吗？

师：我们可以把等式写成这

（出示第二个天平）

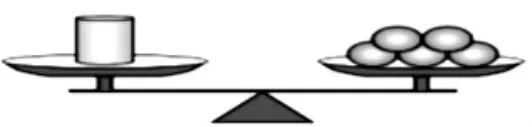
师：仔细观察，你还能写出其他的等式吗？

师：你能理解这些等式表示的意义吗？

【设计意图：教师鼓励学生多角度思考，写出不同的等式，引导学生相互交流，解释意义。在此基础上让学生理一理，归纳出各种不同的等式，培养学生求异思维、以及良好的交流表达能力。】

师：两个圆锥和五个球并没有在同一个天平的两边，那它们怎么会相等呢？

师：你能看懂这个等式吗？和同学说说它表达了什么意思？你觉得它是怎么来的？

生：这个等式是错误的，因为2个圆锥和5个球并没有在天平两边，不能判断相不相等。

生：（指着天平图边指边说）这个等于这个，那个也等于这个，所以它们相等。

生：1个圆柱等于2个圆锥，1个圆柱还等于5个球，所以2个圆锥等于5个球，因为它们都等于一个圆柱的重量（质量）。

【设计意图：让学生在经历观察的过程后，留给学生充足的独立思考和小组间互相讨论时间，让学生好好地想问题。等量代换的内容本身比较抽象，学生理解起来有一定困难，也有一些学生积累了等量代换的初步经验，但不能很准确地表达出来，通过同学间互相讨论、合作交流，明确了圆柱、圆锥和球之间的质量关系，也体会了等量代换的意义。】

小结：因为1个圆柱等于2个圆锥，5个球也等于1个圆柱，所以2个圆锥的质量等于5个球的质量，像这样的变化，在数学上我们把它叫做等量代换。

并表示出等式

揭题：像上面这样的等式，表示积相等的关系，今天我们就来学习《积相等（一）》的等式。（板书课题）

（独立计算，讨论反馈）

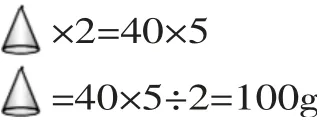
小结：等量可以代换，积相等的算式中有2个未知量，已知其中一个，就可以求出另外一个。

【设计意图：通过新学习的等量代换和之前所学的计算知识相结合来解决一些实际问题，体会到数学与实际生活是相关联的，感受到学习数学的作用。】

师：圆锥数量变化，球的数量也会相应发生变化。你能根据已知的等量关系，推算出4个圆锥等于几个球吗？

师：4个圆锥等于几个球？你是用什么方法求出来的？

生：我看天平左边，圆锥的数量乘2了，右边也可以乘2，所以等于10个球。

生：我把上面天平的2个圆锥看成一组圈起来，5个球也看成一组圈起来，它们相等，下面的天平左边等于上面天平再加一组圆锥，那么天平右边也同样加上一组五个球就行了，等于10个球！

生：天平的左边乘2，右边也乘2，等式还是成立的，所以右边是5×2=10个球。

【设计意图：猜想是学生感知事物后做出初步的未经证实的判断，是学生在成长过程中获取知识的重要环节。两个天平物体数量的变化包含着什么样的规律？问题驱动猜想，把学生的思考进一步引向深入。】

师：大家在天平上说得很好，老师把天平变化成等式，你还能说清理由吗？

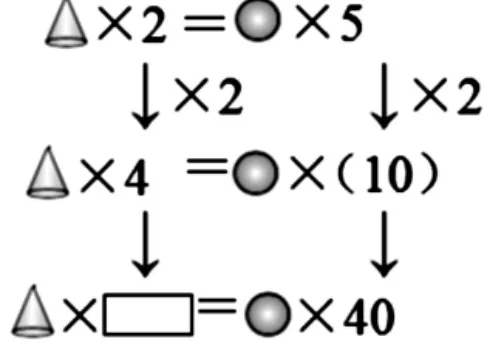
（学生表达从天平抽象到等式的结论）

（学生回答略）

师：观察同学们变出的这些等式，你发现了什么规律？

生：左边乘几，右边也乘几。

生：我觉得他说得不够完整，应该是等式的左边乘几，右边也乘几，等式还是等式。

生：我们从下往上看，也可以理解成等式的左边除以几，右边跟着除以几，等式还是成立的。

生：不一定必须要从第一个等式开始，从中间等式也可以变化到下面的等式的，只要它们有倍数关系就可以。

小结：等式的左边乘几，右边也乘几，等式还是成立的。

【设计意图：学生由具体实物之间的平衡关系抽象、概括出等式的两边同乘几（除以几）等式还是成立的，这是本节课的教学重点，它将为之后系统地学习等式的基本性质打下基础。】

（练习巩固题目略）

三、课堂小结

师：通过本节课的学习你有什么收获？

【反思：张天孝老师说，数学教学要把数学知识作为载体，以数学问题为中心，在解决问题的过程中进行数学思维方式训练，培育学生良好的思维品质和思维能力。在教学过程中要舍得留时间让学生独立思考，并组织学生充分地讨论与交流，为学生提供好好思考问题的空间与时间。教学要尽可能将知识的发生、发展过程详细地展现在学生面前，让学生共同经历这个过程，从中得出结论，只有这样，学生得到的知识才是他自己的。有时候，为了赶时间，我们会不自觉地把知识“教”给学生，本意是想节约一点时间，多做做巩固练习，可是学生掌握的知识并不牢固，根本原因是教师灌输的知识没有转化为学生自己的知识。让学生好好想问题，就要设计出学生愿意参与的学习活动，乐于思考的学习材料。等式的基本性质本身是比较抽象的，从天平的直观到数形结合的等式，抽象程度逐步提高，归纳概括的结论也慢慢升级，学生在其中可以好好地想问题。】