凡欲明一法，必设一题

何月丰

“夫学算者，题从法取，法将题验，凡欲明一法，必设一题。”这句话出自我国南宋时期杰出的数学家杨辉之笔。我第一次读到是在单墫教授所著的《解题研究》一书中，当时甚为惊讶。只是那本书中仅引用这句话，以此佐证题在数学教学中的重要性，对于这句话的具体释义则并未给出。

我带着一点认识，又夹杂着“不甚理解”的遗憾，请教了我县教科所、中学语文特级教师朱益群老师，朱老师给出了如下释义：“学算术，题目依据规律（方法）而命制，规律（方法）又对题目做出验证，凡是想要理解一种规律（方法），必定对应地创设一个题目。”

读罢，心里既兴奋又踏实。兴奋的是这句话所表达的意思如我所愿，踏实的是我的想法得到了更好印证。

这让我联想到了我所从事的小学数学教学工作。为了让学生理解小数乘法的算理和算法，为了让学生理解图形的周长、面积计算公式，为了让学生理解公因数、最大公因数的概念，我们都要创设一道道相关的题目。猛然间发现，在数学教学中，例题不正是“必设一题”的最好证明吗？杨辉的观点我们一直沿用至今，足见其价值。

至此，让我又想起了《这才是好读的数学史》中的一段话：

4000年前的埃及数学已经是相当发达的知识体系，其内容与我们今天所学习的计算和几何的内容非常相似，我们今天的中小学都还在应用。它被记录下来，并通过问题的方式进行教学，这些问题的例子都是可以模仿的。

“通过问题的方式进行教学”不正是“凡欲明一法，必设一题”的体现吗？这无疑进一步证实了题是教学数学的最佳载体，“凡欲明一法，必设一题”是数学教学的最佳方式，且这种方式已经延续了几千年。所以可以得出这样一个结论“凡欲明一法，必设一题”贯穿于整个数学教学的历史中。

现在，我们必须思考另一个问题：题由谁设？

就现在的小学数学教学而言，让学生获得知识的题基本已经由教材编写者设计好了。教材上的题从功能上讲，可以分为例题和习题这样两大类。例题一般使学生发现和理解知识，习题一般使学生对知识的理解与掌握更加深刻和深化。

可以这样说，现在小学数学教材上的题已经比较完备了，主要体现在两个方面：第一是例题的知识体系已经很完备，基本将学生生活和进一步学习数学所必需的基础知识涉及到了；第二是例题后的习题跟进比较完备，作为必要的补充和深化，体现出了逐步提升的层次结构，能帮助学生更好地理解数学。

那么，这是不是说我们现在的小学数学教学，只要按照教材上编排好的这些题，依次按部就班教学即可？从教学实际来看，不是这么简单。也就是说，即使教材编写者设计的题已经比较完备，但教师依旧要根据教学实际需要设计题目。这种设计，主要体现在对习题的改编和创编上。

习题改编，相信很多教师不会感到陌生，因为这在小学数学教学中是一种比较常见的行为，此处不再赘述。

下面，重点谈一下习题创编。从“凡欲明一法，必设一题”可知，每一道数学题的创设，都是有明确目的的，这一点，教材上的每一道题都可证明。所以，教师要创编一道习题，自然也要有明确的目的，这不仅体现了教师对教材的深度理解，还常常体现着教师对数学知识本质的深度把握。下面这个例子可以较好地说明此观点。

【习题创编说明】

平行与垂直是平面内两直线的位置关系。虽然是在一个课时中教学的，但一般是作为两个独立的内容对待的，即平行和垂直各自作为一个教学环节。概念建立后的习题教学，也往往以静态呈现的方式独立看待平行和垂直。这样的习题，对于学生更好地理解和掌握平行与垂直的概念固然有很好的促进作用，是需要的。但是，这样的习题对于理解平行与垂直之间的关系——尤其是两者之间的运动变化关系，始终没有顾及。基于这样的认识，我萌生了要创编一道体现两者关系的习题，意图引导学生从运动变化的视角来看待平行与垂直，更好地理解平行与垂直是平面上两条直线在运动变化过程中某一时刻的定格，是两条直线之间的某一特殊位置关系的表征。

【习题教学描述】

教学时，几何画板上直接出示下图页面。学生观察页面上的两条直线，判断这两条线之间的位置关系——相交。

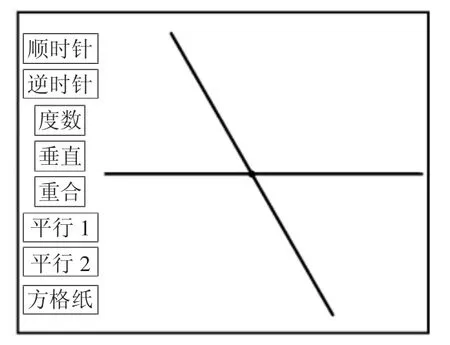
在确认是相交之后，教师提出第一个任务：“如果现在想让这两条直线互相垂直，你有办法吗？”此时学生都能想到：只要把有点“斜”的那一条直线再稍微旋转一下即可（说明：课件边上的按钮是用英文字母代替的，以防给学生暗示）。按照学生的方式，教师将有点“斜”的那条直线顺时针旋转，并请学生观察，提醒教师停止的时间。这个时间点是很难控制的，所以课件上还准备了逆时针的按钮。经过多次调整，在大家都认为是垂直的时候，出示度数验证，如果还不垂直，可通过“垂直”按钮准确实现垂直。（如下图）

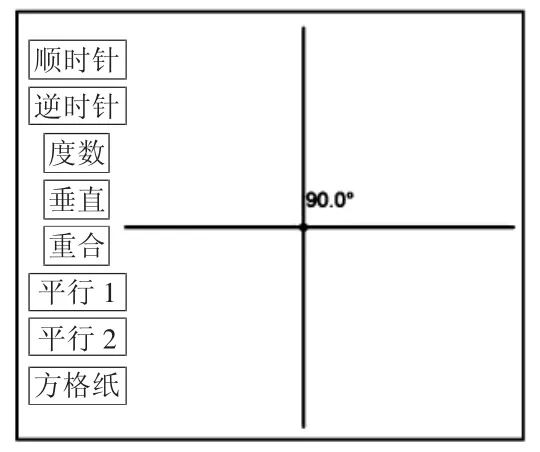
在上述过程中，来回多次调整看似多余，其实是关键，因为正是这个过程，让学生深刻体会到了垂直是两条直线在运动变化中某一特殊时刻的瞬间定格。

完成上述教学之后，教师提出第二个任务：“如果这条直线继续顺时针旋转，会发生什么情况？”这里不着急请学生回答，让学生先想象一下。学生根据想象，会发现继续顺时针旋转，两条直线就会重合。根据学生的想法，教师课件演示，继续顺时针旋转，直到重合。

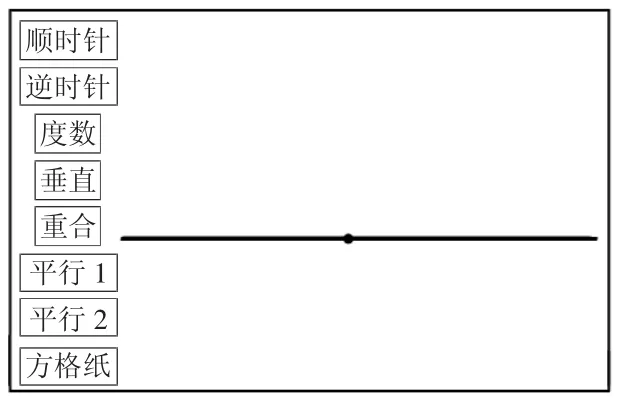
上述教学实现了从相交到重合的运动变化。同样，学生在这个运动变化的过程中就体会到，重合也无非是两条直线在运动变化过程中的一个瞬间定格而已。

完成上述教学之后，教师提出第三个任务：“如果现在想使这两条直线平行，你有办法吗？”学生自然会想到：只要把其中一条直线向下或者向上平移即可。运用学生的方法，课件演示向下平移。为了更好地展现“平行”，可借助方格纸进一步帮助证明。一次平移之后，继续思考：还能不能继续移动？这就是“平行2”按钮的作用了。

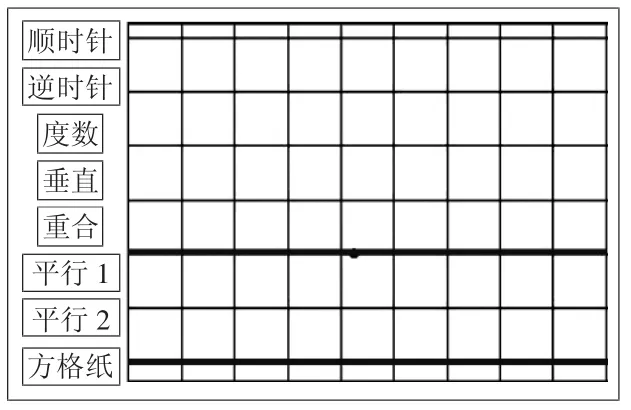
从这道习题的设计和教学可以看出，此题一方面在进一步巩固学生对于平行与垂直的理解，另一方面——也是本题创编的核心目标——引导学生从运动变化的视角看待垂直、重合与平行的关系，加深对平行与垂直的理解。

所以，题由谁设？就我们现在的小学数学教学而言，题主要是由教材编写者设计。但这不是全部，题，也需要作为教学执行者的教师自己来设计。

教材编写者设计的题，是基于数学知识体系的逻辑结构和教学的一般原理考虑的，具有很强的普适性。教师自己设计的题，是基于自己教学的具体实际需要和对数学的自我理解而考虑的，具有很强的个人色彩。当然，两者的目的一定是一致的，都是为了学生能更好地学习数学。

综上所述，作为一线数学教师，不仅要努力做好“习题执行者”这个基础角色，也要努力成为“习题设计者”这个“高光”角色。特别值得一提的是，教师创编习题的过程，也能有效促进自我的专业成长。

“凡欲明一法，必设一题”，于学生，于教师，同样重要。