经历定义的选择过程提高表达和辨析能力
——以《角的认识》一课为例
章剑
【教学内容】
浙教版四年级上册第51、52页《角的认识》。
【教材分析】
教材给出了两种角的定义,从角的静态(从一点引出两条射线所组成的图形叫做角)、动态(角也可以看成是由一条射线绕着它的端点旋转而成的图形)两个方向经历科学、规范、抽象的角的概念的探究过程,是浙教版教材独有的内容。
【教学过程】
一、回忆引入
学生自主作业:什么是角?
(用文字或画图等方法来说明什么是角)
表述一:
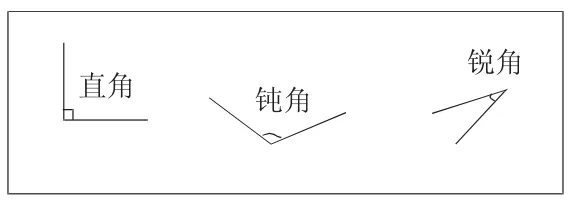
表述二:

表述三:
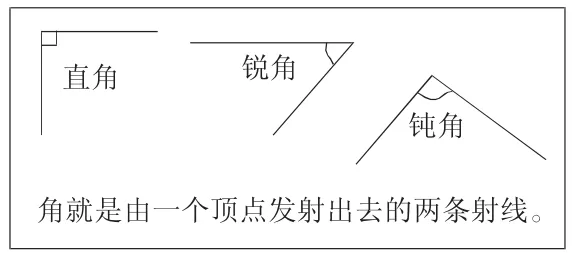
师:画图、文字、图文并茂有什么好的地方?有什么不足的地方?(学生回答略)
师:同学们的见解有什么相同的地方,又有什么不同的地方?
相同:都有一个点,两条线。
不同:角的边有的同学说是线段,有的说是射线。
师:用线段比较好?还是用射线比较好呢?我们可以举一些例子,看看射线和线段谁更合适用来定义角?
【设计意图:回忆什么是角,了解学生角的概念掌握情况。继而,让学生对各种典型的表达进行评价,评价他人的同时,也是对自己概念理解和表达的反思,聚焦认知冲突:角的边(线)到底用射线还是线段来表达,引导学生进行深层次的概念辨析。】
二、探索静态角的概念
1.比较两个滑梯的陡和平。
师:(出示滑梯图)哪个滑梯比较陡?哪个比较平?为什么?

生:右边的滑梯比较陡,因为这条线比较斜。
师:比较斜是什么意思?
生:像滑梯这样比较陡,就是下面这个角比较大;比较平,就是角比较小。
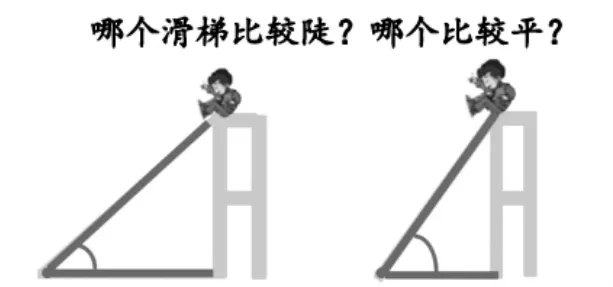
生:张开得大,角比较大,滑梯就比较陡;张开得小,角比较小,滑梯就平。
【设计意图:图中特意增加一条水平线(地平线),帮助学生直观理解所谓“比较斜”“比较陡”,亦可以用地平线和滑梯线组成角的大小来作参照和刻画。】
2.比较三个滑梯的陡和平。
师:这里有三个滑梯,比较一下哪个滑梯最陡?

生:一样陡。
生:第一个最陡。
生:第三个最陡。
师:有什么方法能清楚地知道哪个滑梯更陡?
生:可以通过重叠来比一比。
师:(演示课件重叠)哪个滑梯更陡?重叠以后你发现了什么?
生:滑梯的高矮不一样,长短不一样,但角的大小没有变,其实是一样陡的。
师:如果滑梯的两条边更长,那么角的大小?两条边再变长呢?
生:两条边线不管怎么延长,角的大小不变。所以,两条边以射线表达更好。
【设计意图:在学生熟悉的滑梯情境里,帮助学生直观感知边的长度增加不影响角的大小。呼应学生前测作品中的困惑,角的大小既然与边的长度无关,则两边可以往一个方向无限延长,用射线定义角更加合适。】
师:角的大小和两边张开大小有关,而和边的长短无关。所以我们定义角用——
生:用射线比较好。角的两边可以无限延长。
【设计意图:本课要学习的静态角的概念和三年级直观认识角的组成比较接近,将重点放在学生困惑的问题上:角的两边用线段还是射线来定义好?创设滑梯情境,引导学生借助直观经验,自主辨析明理,突破知识难点。同时,也有助于学生形成良好的学习信念:一切定义都有道理可循。】
三、探索动态角的概念
师:钱江新城的灯光秀上有两个探照灯扫射形成了角——你会怎样描述这个角的形成呢?
生:我觉得,这可以想象成一条射线绕着它的端点旋转,形成了很多个角。
生:灯的位置就是射线的端点,射出的灯光就是一条射线,射线绕着端点慢慢旋转,来到新的位置,和原来位置的射线形成了角。
师:真棒!我们除了可以从静态角度分析角的组成,也可以从动态角度观察。动态角是怎么形成的?请用手比划一下。
【设计意图:动态角的认识角度比较新颖,对于学生来说,比较陌生和抽象。设计探照灯扫射成角的场景,激活学生已有的生活经验,激发动态想象。学生通过观察探照灯扫射是如何形成角的,理解到一条射线绕着它的端点旋转,可以形成各种各样的角。最后,通过用手比划,将动态角的形成形象化。】
四、探索读角写角的方法
师:你能比较这两个动态角的大小吗?有什么好办法让别人一听就明白你在说哪一个角呢?
生:可以把一个角叫角1,一个角叫角2。
生:可以把一个角叫角A,一个角叫角B。
依言标上数字和字母——
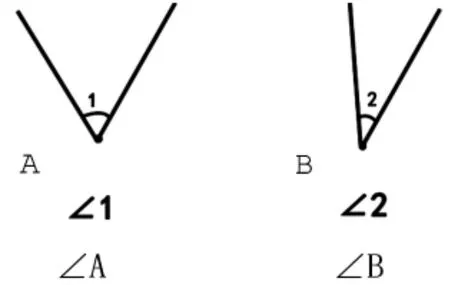
师:如果共用一个顶点的角有好几个,怎样区分呢?
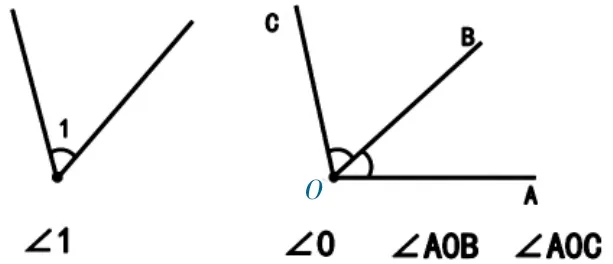
引导讨论:仅用顶点字母无法区分,只能添加边上的字母——顶点字母放在中间。
师:你知道怎么画角吗?画一个角,给画好的角取一个名字。
生:画两条射线,这两条射线要从一个点出发。
生:先画一个顶点,再从一个顶点出发画两条射线。
生:可以用数字或者字母来标记角,顶点字母放中间。
【设计意图:数学常识的教学也要给学生自主创造和辨析的机会。创设几个角共用顶点的情境,引导探讨如何表示这些角,自然地想到要用其他相关字母。再从角的字母表示思考,从所示符号中,能看出角的顶点吗?能看出角的边吗?进一步体会书写规则的合理性。】
五、探索判断角、比较角的方法
1.找直角。
师:用一个圆片,不借助其他工具,你能创造出一个直角吗?
生:像这样将一个圆对折又对折得到的角就是直角。
师:你在哪里见过直角?
生:三角板上有直角。
生:我们刚才做的活动角也可以变成一个直角。
生:数学书上有直角。
2.判断活动角。
师:怎么判断在活动角上找到的角是直角呢?
生:用三角尺上的直角,或用圆折出的直角比,如果角的两条边都和标准的直角重叠了,就是直角。
师:怎么判断锐角和钝角呢?
生:顶点重合,一条边(始边)重叠,另一条边(终边)在直角边里面就是锐角;另一条边(终边)在直角边外面就是钝角。
动态演示:观察射线旋转到什么位置形成直角、锐角和钝角?
3.巩固练习。
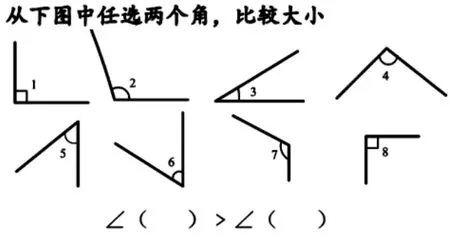
(1)直接目测比较:钝角>直角>锐角。
(2)同样是锐角或者钝角,怎样比较大小呢?
重叠法比较:借助活动角比较∠2和∠7或∠5和∠6的大小。
(3)如果没有活动角,我们还能怎么比较角的大小?(量角器)
【设计意图:从特殊的直角开始形成重叠(重合)比较的经验,进一步推广到一般角的比较。利用活动角来判断角,在应用中再认识动态角,突破教学难点。在此基础上,初步渗透量角器的测量原理,量角的过程就是与量角器上对应角重合的过程。】
六、小结
师:今天这节课学了什么?什么叫角呢?
师:这是个静态角,你能把它看成动态角吗?
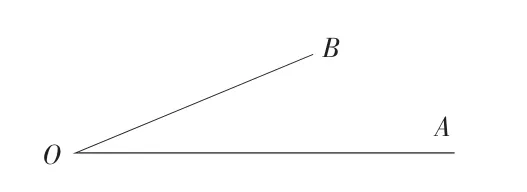
生:角AOB可以看作是动态角,就是射线OA绕着它的顶点O旋转到OB的位置所形成的角。
【设计意图:小结中体现了学生理解和表达的四个水平层次,水平1:能用自己的语言来描述角;水平2:能用静态角或动态角的定义来描述角;水平3:能用静态角和动态角的定义从不同角度来描述角;水平4:能将静态角转化成动态角。】
【课例综述】
概念教学常常比较枯燥,如何让学生有兴趣学,而且还能发展高阶思维,提升数学素养,本课尝试从以下两方面来实现。
一、重视学生数学表达能力的培养
语言是思维的外壳。数学语言能力与数学思维互为表里,息息相关。关注学生的表达:通过倾听学生的表达,了解他们的思维水平;通过改进学生的表达,提升他们的认知深度。具体来说:1.引入环节。回忆什么是角,用文字、画图等方法来说明什么是角?侧重于书面的、形象的表征。2.判断角,比较角,让学生利用三角尺中的直角、圆上的直角、活动角等来说明判断的依据。3.小结环节。课的最后,学生对“什么是角”的表述体现了他们理解和表达能力的四个水平层次。
二、重视学生数学辨析能力的培养
数学概念往往基于具体、形象而又要超越直观,作出理性的抽象,为进一步推理、生发新概念、新命题做准备。教学中,积极创设学生熟悉的生活情境,在此基础上引导学生反思、想象,辨析数学概念。具体来说:1.聚焦认知冲突,通过滑梯陡峭程度的讨论,理解为什么用“射线”定义角。2.创设灯光秀情境,感知角的动态形成,突破角的动态定义。3.创设共用顶点角的情境,深化讨论角的表示方法,感悟数学规定的合理、简洁。4.从判断直角到测量角的度数,聚焦边的重合情况,体会角的大小的本质。

