数形结合百般好
——《点阵中的规律》教学实录(一)
洪乔
【教学内容】
北师大版五年级上册第98页。
【教学过程】
一、计算比赛,激趣导入
师:先来做个小调查,咱们班谁计算速度最快?谁动作最快?
(选一位学生速算,再选一位学生用计算器计算,与教师比赛)
师:请看大屏幕中的题,任选其中一题进行比赛。其他同学看清楚了,你们是评委哦!

(比赛结果:教师获胜)
师:想知道获胜的秘诀吗?
生:想。
师:老师把这道计算题转化成了一个正方形点阵,只要用一句乘法口诀就能很快地算出答案,这种学习数学的方法叫做数形结合。(板书)
二、化难为易,获得经验
1.揭示数点数要找规律。(动画依次呈现三角形点阵)

师:我们一起来数一数,这些图形是由几个点组成的?
生:第一个点阵是由1个点,第二个点阵由3个点,第三个点阵由6个点,第四个点阵由10个点,第五个点阵?第六个?第七个?
师:声音怎么不整齐了?怎么回答不出来了?原来咱们还没有发现其中的规律,今天我们就来学习点阵中的规律。(板书)
2.探索点阵内分组找规律的方法。
师:第三个点阵是怎么数的?
生:横着数1+2+3=6。
生:斜着数也是1+2+3=6。
(学生回答的同时,教师用课件的荧光笔涂色,进行分组)
师:我们从上往下观察这些点阵,你有什么发现?
生:从上往下看每个点阵,一层比一层多一个点。
师:我们再从左往右观察每个点阵的算式,你又有什么发现?
生:从左往右看每个算式,后一个加数比前一个加数多一。
师:这些算式都是由点阵得到的,我们一起来说一说吧。
齐说:第一个点阵是1,第二个点阵是1+2,第三个点阵是1+2+3,第四个点阵是1+2+3+4,第五个点阵是1+2+3+4+5,……第N个点阵是1+2+3+……+N。
师:第七个点阵的算式应该从1一直加到几?怎样列式?
生:从1一直加到7,算式是1+2+3+4+5+6+7。
小结:对于这组三角形点阵,我们可以任取一个三角形采用分组的方法来研究,发现点阵中的规律是:一层比一层多一,那么相对应的算式中的规律是:从1开始,后面一个加数比前面一个加数依次多一,是第几个点阵就加到几。
三、自主探究,构建模型
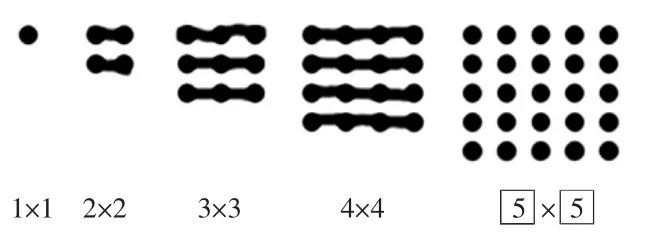
师:请拿出学习卡。这是一组正方形点阵,请同桌两人共同探索规律,写出相应的算式,并说说点阵与算式之间的规律。

(同桌两人运用所学知识,共同探讨规律,教师巡视,手机拍照展示学生的探索结果)
1.横着看,找规律。
师:说说你是怎么找规律的?
生:我是横着看找规律的,第一个点阵是1个1,所以列式1×1;第二个点阵是2个2,所以列式是2×2;第三个点阵是3个3,所以列式是3×3;第四个点阵是4个4,所以列式是4×4。
(课件同步演示:1×1,2×2,3×3,4×4)
师:那么第八个点阵的算式怎样列呢?有多少个点?
生:8×8=64。
师:这个正方形点阵与算式之间有什么联系吗?
生:第一个点阵是1×1,第二个点阵是2×2,第三个点阵是3×3,第四个点阵是4×4……第N个点阵是N×N,第几个点阵算式就是几乘几。
2.斜着看,找规律。
师:还有不同的方法吗?
生:斜着看,找规律,第一个点阵是1,第二个点阵是1+2+1,第三个点阵是1+2+3+2+1,第四个点阵是1+2+3+4+3+2+1。(学生边说教师边同步出示算式)

师:仔细观察第三个点阵,我们把正方形沿对角线分成了两个三角形,就成了我们之前研究的三角形点阵,谁知道正方形的这条对角线的点数对应在算式里的什么数吗?
生:对应算式里的3。
师:谁能说说点阵与算式之间的规律?
生:点阵中的点数依次多一,然后又依次减一。相对应的算式也是依次加一,然后又依次减一。
师:还有不同的发现吗?
生:第二个点阵最大数是2,第三个点阵最大数是3,第四个点阵最大数是4……那么第N个点阵最大加数就是N。
师:谁能说说第五个点阵相对应的算式吗?
生:1+2+3+4+5+4+3+2+1。
3.拐弯看,找规律。
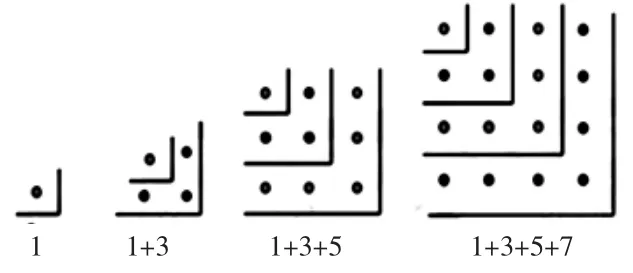
师:这组正方形点阵,你还能列出不一样的分组方法吗?
(展示学生拐弯分的涂色方法,并课件动画出示1个点、3个点、5个点、7个点,最后组成了正方形点阵)
师:你会根据这种分法列出相应的算式吗?
生:第二个算式是1+3,第三个算式是1+3+5,第四个算式是1+3+5+7。
师:你发现算式中各数有什么特点吗?
生:是一组连续奇数的和。
师:再观察点阵与算式之间有什么规律吗?(如果学生发现不了,可以启发:图形被折线分成了几组?所以算式中就有几个数?)
生:第二个点阵被分成了2组,所以算式中有2个数相加。第三个点阵被分成了3组,所以算式中有3个数相加。第四个点阵被分成了4组,所以算式中有4个数相加。
师:第N个点阵,就是从1开始的N个连续奇数相加。
师:刚才我们是在同一个点阵内找规律的。我们还可以与前一个点阵比较来看,还有其他找规律的方法吗?
生:发现第二个点阵比前面一个点阵新增了3个点,所以在前一个点阵的算式后面加3。第三个点阵比前面的点阵新增了5个点,所以在前一个点阵的算式后面加5。第四个点阵比前面一个点阵新增了7个点,所以在前一个点阵的算式后面加7。
师:原来我们横向比较也能发现规律,列出相对应的算式。现在老师要来考考你们了,第五个点阵相对应的算式谁会列?
生:1+3+5+7+9。
四、揭示秘诀,固化新知
1.探索三个算式间的联系。
师:(结合板书)横着看,列式是4×4;斜着看,列式是1+2+3+4+3+2+1;拐弯看,列式是1+3+5+7,结果都是多少?为什么?
生:16,都是同一个点阵。
生:把后两个算式通过移多补少或重新配对可变成4个4。
师:这三种方法中,你最喜欢哪种分法?为什么?
生:第一种,计算最简便。
2.揭示比赛获胜秘诀。
师:这些算式都是同一个正方形点阵,所以在计算时,老师把这些算式都转化成了正方形的第一种分法,直接用乘法口诀4×4=16,就很快算出答案了。你现在知道前面人机大战老师获胜的秘诀了吗?
生:老师都是看算式想是几乘几的点阵,是几乘几的点阵就用几乘几算出结果。
师:大家说一说人机大战中六个算式各是几乘几的点阵?
3.小结。
师:原来数形结合可以这么巧妙地解决数学问题,难怪中国现代“数学之父”华罗庚用他朴素的语言作了一首七言绝句。(课件展示)

五、延伸应用,形成策略
1.我们来看一看这道题:比一比,看谁算得又对又快。
课件出示:
(1)1+2+3+……+20+……+3+2+1
生:都等于20×20=400。
师:看到这样的算式,你能想到什么样的点阵呢?
生:一排20个点,共有20排。
2.请按长方形点阵中的规律填空。

六、联系生活,结课欣赏
1.欣赏图片。

2.请你设计一个点阵,看你的爸爸、妈妈或同学能不能找出你设计的规律?

