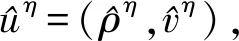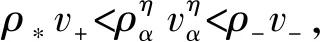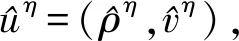关于耦合交通流Aw-Rascle模型Riemann问题
王文雷,潘丽君
(南京航空航天大学理学院,江苏 南京 210016)
2000年,RASCLE和AW提出了二阶交通流模型[1]:
(1)
其中:ρ≥0代表车流密度,即表示单位长度有多少辆车辆;v≥0代表地点行车速度,即某个特定车辆的速度[2-5];标量η>0是微观中对应车辆的加速与减速的加权[6];变量w代表优先速度;压强项p(ρ)为一个预期因子.这里假设p(ρ)满足:
p(ρ)=ργ,γ>0,
(2)
所以对∀ρ有ρp″(ρ)+2p′(ρ)>0,又由文献[7]可知标量η越小,密度ρ越大,交通事故的发生概率也变大.
现实生活中,司机可能会出现一段时间走神的现象,即大脑突然空白这种短暂的无意识阶段,为了描述这一现象并预测交通事故,2010年HERTY和SCHLEPER提出了下面的耦合Aw-Rascle(AR)交通模型[7].
x<0:
(3)
x>0:

(4)
耦合条件:
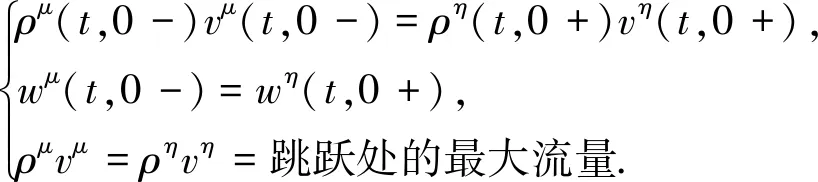
(5)
其中μ<η.将x<0路段记为μ路段,将x>0路段记为η路段,如图1所示.

图1 暂时失去意识驾驶人士的道路网络(μ<η)
耦合交通模型(5) 中的第一个方程表示质量守恒,第二个方程表示动量守恒,第三个方程表示两条路段交汇处的最大车流量,更多细节可以参考文献[1,6,8-9].针对上面的耦合模型(3)-(5)的黎曼问题,HERTY 和SCHLEPER在文献[7]证明了解的存在性,但是没有给出显式解.此外,在μ→0的条件下,他们证明了带有如下初值

(6)
耦合交通模型(3)-(5)的解的唯一.
本文仍然研究耦合AR交通模型(3)-(5)带有初值(6)的黎曼问题.根据不同的情况,利用特征分析法和相变的相关理论,详细构造出耦合AR模型黎曼问题的显式解,并且在无μ→0的条件下,证明了黎曼解的唯一性.
1 基础知识
系统(1)的特征值为:
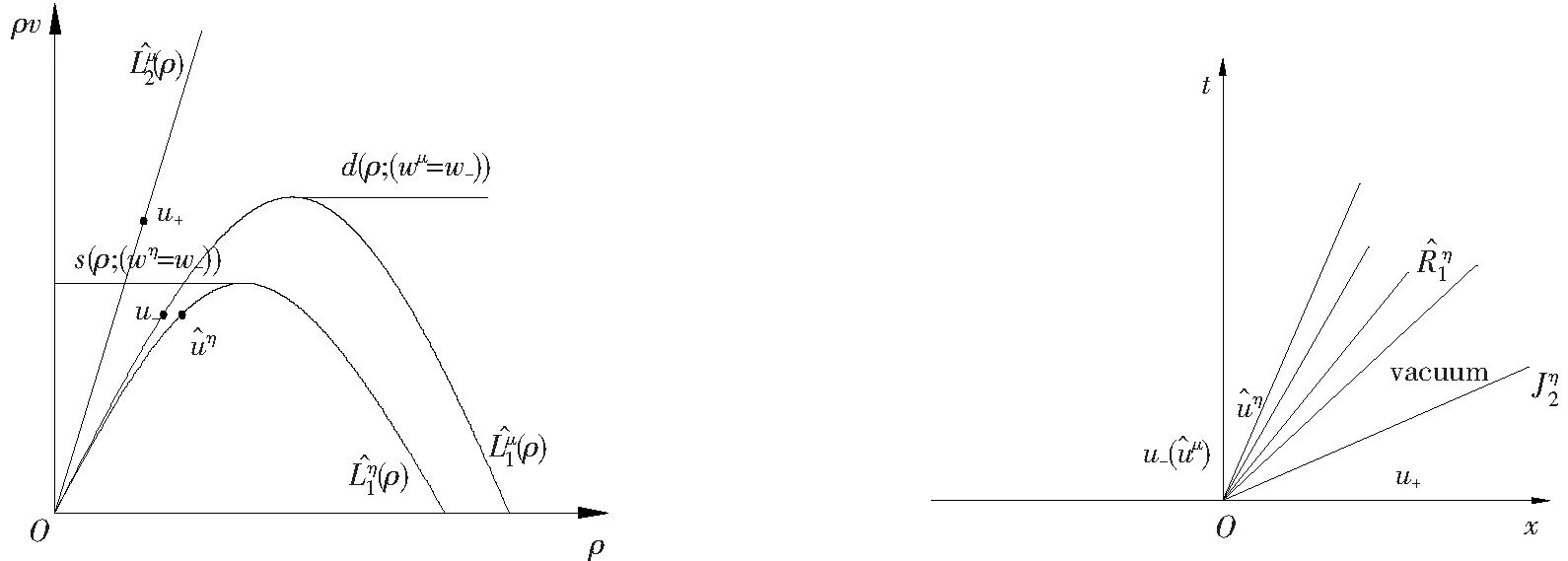
λ1=v-ηρp′(ρ) 故系统(1)是严格双曲的,对应的特征向量为: 第1-Riemann不变量w和第2-Riemann不变量z分别为: w=v+ηp(ρ),z=v. (9) 为表达方便,需引进一些记号.记 图2 曲线曲线和曲线的数学性质在平面(ρ,ρv)表达 经过简单的计算得到: 需求函数为 d(ρ;(wμ=w-))= (10) 供给函数为 s(ρ;(wη=w-))= (11) 此时条件(5)的第三个方程变为 ρμvμ=ρηvη= min{s(ρ*;{wη=w-}),d(ρ-;{wμ=w-})}[7], 耦合条件(5)可以改写为 (12) 本节,根据不同情况详细讨论耦合AR交通模型(3)—(6)的 Riemann问题,利用特征分析法和相变的相关理论构造出上述问题的显式解,并讨论解的唯一性. 在(x,t)平面上,由AR交通模型的特征值λ1和λ2,可以先粗略地表示出Riemann问题(3)—(6)解的结构[7],如图3所示. 图3 在(x,t)平面上粗略表示Riemann问题波的形式 在μ-路上左状态u-=(ρ-,v-)先通过负波连接到状态uμ=(ρμ,vμ),再通过耦合条件跳跃到η-路上的状态uη=(ρη,vη),此时状态uη=(ρη,vη)通过正波连接到中间状态u*=(ρ*,v*),最后中间状态u*通过正波连接到右状态u+=(ρ+,v+). (13) (14) (15) (16) (17) CaseⅠv+ CaseⅠ.1s(ρ*;{wη=w-}) SubcaseⅠ.1.1ρ*v+<ρ-v-. (18) 图4 在(ρ,ρv)平面和平面(x,t)中表示在跳跃处的黎曼问题解 图5 在(ρ,ρv)平面和平面(x,t)中表示在跳跃处的黎曼问题解 (19) 图6 在(ρ,ρv)平面和平面(x,t)中表示在跳跃处的黎曼问题解 SubcaseⅠ.1.2ρ*v+>ρ-v- (20) 图7 在(ρ,ρv)平面和平面(x,t)中表示在跳跃处的黎曼问题解 (21) 图8 在(ρ,ρv)平面和平面(x,t)中表示在跳跃处的黎曼问题解 CaseⅠ.2s(ρ*;{wη=w-})>d(ρ-;{wμ=w-}). SubcaseⅠ.2.1ρ-v-<ρ*v+. (22) 图9 在(ρ,ρv)平面和平面(x,t)中表示在跳跃处的黎曼问题解(ρ-v-<ρ*v+) SubcaseⅠ.2.2ρ-v->ρ*v+. 如图10所示,此时该Riemann问题的解结构为 CaseⅡv+>v-+μp(ρ-). CaseⅡ.1s(ρ*;{wη=w-}) u0=(ρ0,v0)≜(0,v-+μp(ρ-)). (23) (24) 此时的Riemann问题的解结构为 (25) 图10 在(ρ,ρv)平面和平面(x,t)表示在跳跃处的黎曼问题解(ρ-v->ρ*v+) 图11 在(ρ,ρv)平面和平面(x,t)中表示在跳跃处的黎曼问题解 图12 在(ρ,ρv)平面和平面(x,t)中表示在跳跃处的黎曼问题解 CaseⅡ.2s(ρ*;{wη=w-})>d(ρ-;{wμ=w-}). (26) 图13 在(ρ,ρv)平面和平面(x,t)中表示在跳跃处的黎曼问题解 注对于情况Case Ⅱ.2,HERTY和SCHLEPER在文献[7]中证明了μ趋于0时,耦合AR交通模型黎曼解具有唯一性,而本文无需满足该条件. 综上,Riemann问题(3)—(6)的显式解已经完全获得,于是得出如下定理: 定理给定初值(6),如果μ<η,则耦合AR交通模型(3)—(5)的Riemann解存在且唯一.

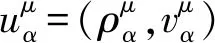
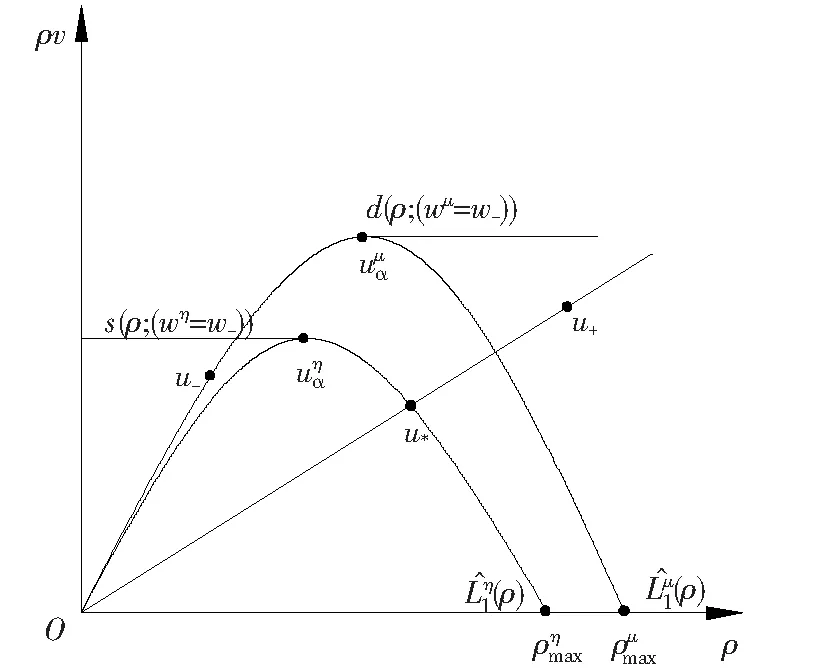



2 Riemann问题的显式解及其唯一性