开放世界信息更新的逻辑系统

曹发生

(1.中山大学 逻辑与认知研究所,广东 广州 510275;2.贵州民族大学认知科学与技术系,贵州 贵阳 550025)

知识或人的智能很多时候表现为分类的能力.一个简单的例子，从房间里打开门走出来，这里就得区分墙与门.从抽象的意义上来讲，知识构成了某个领域中的各种分类模式的一个集簇.有些知识系统不难被人们描述而掌握，有些新生事物则没那么容易被刻画.以2003年出现的新事物SARS(严重急性呼吸综合症Severe Acute Respiratory Syndrome) 为例，刚开始时候不知道它到底属于哪一种类型肺炎,用原有的知识很难描述，于是要打破传统的封闭世界预设，建立开放世界预设.李未在文献[1]中建立了一阶开放的逻辑系统，用来刻画知识的增长、更新和假说的进化.他将假说序列看成对力学的认识的进程，在论文的结束语中指出： 开放逻辑将在机器学习、知识获取及数据库维修方面有着广阔的应用.鞠实儿[2]详细给出开放类的存在性的论述.我们结合粗糙集逻辑决策逻辑和文献[2]对开放类的刻画建立开放世界信息更新的逻辑系统.随着信息的更新,发现 SARS 是一种非典型肺炎，用本文语言描述就形式化为：(φ→P*)→[(φ,c1,vc1′);(φ,c2,vc2′);...;(φ,ck,vck′)]P.

文献[2-3]给出开放类的定义如下:

设q为任意一阶谓词,它表达性质Q.一个类Q是W上的开放类，当且仅当它满足如下条件：

(i)Q={x|x具有Q性质,x∈W}={x|q(x),x∈W}；

(ii)在潜在世界WR中可能存在一个体a,a具有性质Q.

鞠实儿在文献[2]以肺炎概念知识为例，将整个知识范畴划分为：

粗糙集理论中的知识表达方式一般采用信息表或称为信息系统的形式，用信息表来刻画粗糙逻辑和决策逻辑的语义[4-11].信息表就已经设定这个映射是满射，为了解决部分映射或非满射情况，我们提出开放信息系统，更一般的映射取代信息表恰好为建立开放信息系统的语义提供了坚实的理论基础.

1 开放世界信息系统

一方面我们要将实例抽象到理论高度，另一方面想把信息表这个映射推广到部分映射或非满映射上来.出于这两方面考虑，本文的目标是把开放世界形式化，给出开放世界信息更新的逻辑系统.

下面给出开放世界信息系统的定义.

定义1 一个开放世界信息系统S是一个多元组S=(W,A,VA∪{},f,{Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I).其中:

(1)W是对象的非空集合，称为论域；

(2)A是属性的非空集合；

(3)VA=∪a∈AVa,Va是属性a的值域，其元素也称为关于属性a的属性值，或简称为属性值；

(4)f:W×A→VA∪{}是一个映射，即对每一个对象的任意属性都赋予了一个属性值；

(5)I是有穷指标集合对于每一个i∈I有下面的成立:

(a)Bi,CBi,DBi⊆A是一些特殊的属性集合，称为开放属性集合，这些属性可以用来给出开放世界中的概念的刻画；

(b)VBi,VCi′,VCi″,VDi分别是属性集合Bi,CBi,CBi,DBi中特殊的属性值集合，使得

(i)VBi={vb∈Vb|b∈Bi} ；

(ii)VCi′={vc′∈Vc|c∈CBi}，VCi″={vc″∈Vc|c∈CBi}使得对任意的c∈CBi都有vc′≠vc″；

(iii)VDi={vd∈Vd|d∈DBi}；

(i)Pi={x∈W|对于每一个b∈Bi有f(x,b)=vb并且对于每一个c∈CBi有f(x,c)=vc′}；

(iv)Ui={x∈W|对于每一个b∈Bi有f(x,b)=vb并且存在c∈CBi有f(x,c)≠vc′,并且存在c∈CBi有f(x,c)≠vc″,并且存在d∈DBi有f(x,d)≠vd}；

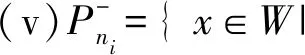
经典的信息系统中f:W×A→V是一个映射，如果它是一个部分映射(这里部分映射的定义可以参考文献[12])，我们通过将未给定义的原像引入一个新的表示未知属性值的符号作为这些原像的像，补充成为映射.这里表示开放世界中知识的该属性值还未被认知.接下来引入开放世界信息系统的信息映射的定义.

定义2 设f:W×A→V∪{}是一个映射，可以定义一个映射m:A×V∪{} →2W，m(a,v)={x|f(x,a)=v}.(f可以不是满射，若v无原像则m(a,v)=∅.)

由映射m:A×V∪{} →2W，也可以定义f:W×A→V∪{},其中f(x,a)=v，若x∈m(a,v).此时f也记为fm，m也记为mf.

2 开放世界信息更新的逻辑系统

开放世界信息更新的逻辑LSOWIS语言L采用PAWLAK在文献[6]及KHAN等在文献[9]中给出的方式定义.

2.1 语法

定义3 开放世界信息系统更新的逻辑LSOWIS语言L的字母表包括以下部分：

(1)可数无穷集合OC，其元素称为个体常元，用x,y,z或加数字下标表示；

(2)可数无穷集合AC，其元素称为属性常元，用a,b,c,d或加数字下标表示；

(3)集合AC的子集合符号，用B,C,D或加下标表示；

(6)信息算子符号;(合成算子),∨(选择算子)；

(8)合式公式变元符号，用α,β,γ或加数字下标表示；

(9)命题变元符号集合PV，其元素用符号p或加数字下标表示；

(10)技术性符号(,),[,].

定义4 信息的形成规则：

(1)每一个原子信息(φ,a,v)是信息，这里φ是下面定义中的合式公式；

(2)若σ，σ′是信息，则σ;σ′和σ∨σ′都是信息；

(3)仅由以上2条形成信息.

定义5 开放世界信息更新的逻辑LSOWIS语言L的合式公式的形成规则：

(2)(a,v)是合式公式，称为描述子；

(3)若α,β是合式公式，则α,α∧β,[σ]α是合式公式；

(4)仅由以上3条形成合式公式.

全体描述子的集合记为D，全体合式公式的集合记为P，记Pfini为每一个属性集合符号B仅仅含有穷多个属性的全体合式公式.除去形成规则(3)中的构造方式[σ]α而得到的公式也称为布尔合式公式.

下文中的合式公式α∨β定义为(α∧β);合式公式α→β定义为(α∨β);合式公式α∨β定义为(α→β)∧ (β→α).

2.2 语义

开放世界信息更新的逻辑LSOWIS语言L的语义是基于模态逻辑[13]的模型结构的.

定义6 一个模型M 是一个多元组M=(W,A,VA∪ {}, {Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I,m,V). 其中

(1)m:D→2W；

(2)多元组(W,A,VA∪ {},f, {Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I)是一个开放世界信息系统，其中f是由m按定义2所对应映射；

(3)V:PV→2W.

模型结构M也可以诱导出一个开放世界信息系统，这个开放世界信息系统也记为SM.

给定开放世界信息系统S=(W,A,VA∪ {},f, {Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I)，它本质上是语义的，自然地就有语言L下的一套语法系统.下文中提到开放世界信息系统S=(W,A,VA∪ {},f, {Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I)后就将开放世界信息系统的语义符号和语言的语法符号用了同样的形式字符表示，这并不影响理解本文的内容.

定义7 给定开放世界信息系统S=(W,A,VA∪ {},f, {Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I). 定义信息系统的框架SS=(W,A,VA∪ {},{Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I,m)，其中m是由f按定义2所对应映射.模型结构(SS,V)也记为MS.

为了给出一类开放世界信息更新系统，我们要引入一个重要的概念，即开放世界信息系统的相容信息.本文给出的开放世界信息更新系统就是建立在相容信息上的更新.

定义8 设多元组S=(W,A,VA∪ {},f,{Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I)是一个开放世界信息系统.(φ,a,v)是一个关于开放属性a的信息，称它是S的相容信息，如果对于任意的x∈φMS都有f(x,a)=.

定义9 给定开放世界信息系统的模型M=(W,A,VA∪ {}, {Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I,m,V)，定义由原子信息I=(φ,a,v)更新模型M所得模型，或称为M的I更新模型，记为

MI=(W,A,VA∪ {}, {Bi,VBi,VCi′,VCi″,DBi,VDi,}i∈I,mI,V)：

mI如下给出：

当a不是开放属性时:

mI(a′,v′):=m(a′,v′),当a′≠a时;

mI(a,v′):=m(a,v′)φM,当v′≠v时;

mI(a,v):=m(a,v) ∪φM;

当a是开放属性时，当信息I=(φ,a,v)和SM是相容的：

mI(a′,v′):=m(a′,v′),当a′≠a时;

mI(a,v′):=m(a,v′)φM,当v′≠v时;

mI(a,v):=m(a,v) ∪φM;

当a是开放属性时，当信息I=(φ,a,v)和SM不是相容的：

mI(b,v′):=m(b,v′),对于任意的b时;

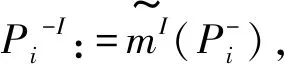
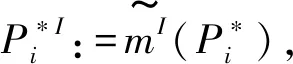
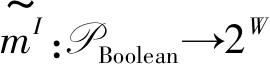
给定开放世界信息系统的模型M=(W,A,VA∪ {}, {Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I,m,V)，给定原子信息I=(φ,a,v)，那么更新模型MI的本质理解如下：

注2fmI是由fm只改变序对(x,a)的像(这里x∈φM)而得到，具体是经过下面变化而得到的：对于个体x∈φM和开放属性a的序对(x,a),若在fm下已经有非像，就将这个像定位这个序对在fmI下的像.序对(x,a),若在fm下的像是，则这个序对在fmI下的像为v. 通俗地讲，是指个体x的开放属性a的属性值已经被认知就不能再改变，没有认知的属性值就由这个信息中的v来定出属性值.对于非开放属性a，这个序对在fmI下的像为v.通俗地讲，是指个体x的非开放属性a的属性值可以改变，其属性值就由这个信息中的v来定.

注2有助于第3节的可靠性定理中关于A15的证明的理解.

由定理1可知，定义9是合理的.

下面定义关于信息σ的模型间的二元关系Rσ，用花体R来区别W上的二元关系R，但都是集合论中的二元关系.

定义10 M RσM′归纳于σ的结构如下：

(1) M RIM′当且仅当M′=MI；

(2) M Rσ；σ′M′当且仅当存在模型M″,使得M RσM″ 且M″ Rσ′ M′；

(3) M Rσ ∨ σ′M′当且仅当M RσM′ 或者M Rσ′M′.

下面给出开放世界信息更新逻辑系统的合式公式在模型中的可满足性的定义：

定义11 任给语言L中的合式公式α如下归纳定义模型M在w∈W上可满足，记为M,wα:

(1)M,w；

(2)非M,w⊥；

(3)M,w(a,v)当且仅当w∈m(a,v)；

(4)M,wp当且仅当w∈V(p)；

(5)M,wα当且仅当非M,wα；

(6)M,wα∧β当且仅当M,wα并且M,wβ；

(7)对于任意信息σ，M,w[σ]α当且仅当对任意的MRσM′的 M′都有M′,wα.

注3 M,wα∨β当且仅当M,wα或者M,wβ；M,wα→β,当且仅当，若M,wα则M,wβ.

有了上面的准备工作就可以给出开放世界信息系统更新的逻辑系统的合式公式的有效性的定义.

定义12 任给语言L中的合式公式α，称α在模型M上是可满足的，如果对于任意的w∈W都有，M,wα.称α是有效的，如果对于任意的模型M中α是可满足的.

下文记αM={x|M,xα}.

定义13 给定语言L的开放世界信息系统的S=(W,A,VA∪ {},f, {Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I)，离散时间序列N的可列个模型{Mi|i∈N}是开放世界信息系统随着信息更新而变化得到的一列模型，如果M0=MS,则称这个模型序列(记为MS)为该开放世界信息系统的在离散时间序列上的更新模型序列，简称为该开放世界信息系统的模型序列(在不强调信息系统的时候也简记为M).在M上定义一个先后次序关系≥，M′≥ M当且仅当存在i,j使得M′=Mi,M= Mj且i≥j.

下面表明这样给出的系统中存在真正的开放类.为了把鞠实儿给出的开放类的定义的2条性质着重刻画出来，将开放类(a,v)M=m(a,v)={x|M,x(a,v)} 定义如下：

(i) (a,v)M= {x|∃M′≥ M,M′,x(a,v),x∈W(a,)M}(记性质“∃M′≥ M,M′,x(a,v)”为Q性质),

(ii)在潜在世界(a,)M中可能存在一个体y,y具有性质Q.

不难验证{x|M,x(a,v)}={x|∃M′≥ M,M′,x(a,v),x∈W(a,)M}，从而(a,v)M确实是一个开放类.

接下来剖析如此定义的开放系统的模型的本质属性.由开放类的定义可以得到本文描述的开放系统的模型具有的一个本质属性：

性质1 给定开放世界信息系统的模型序列{MS={Mi|i∈}，那么这些模型必然满足下列开放信息系统条件:对于任给的M′, M∈MS，若M′≥ M，则且

从数学的角度来考察开放世界信息系统S=(W,A,VA∪{},f, {Bi,VBi,VCi′,VCi″,DBi,VDi,Pni}i∈I)中这个映射f的定义.首先如果f是个部分映射，也即是存在个体x和属性a,它们的组合(x,a)没有像，即个体x的属性a的属性值还未知，只要引入一个未知值符号，就可以将部分映射扩展成为映射.引入符号后不妨设f为映射,这也是在表示开放系统的时候引入的原因.在各种类型信息系统[4-9]中f表示的是一个信息表，信息表就预设了它是个满映射.如果它不是满映射情况又会如何呢？某个属性a的属性值v在当前的信息系统下没有原像，意味着在这个模型下，该属性值还没被人们认知.但是可能在信息更新后的系统中这个属性值v有原像，即更新后的模型下属性值v才被真正认识到，即表明：对于属性a来说，随着时间的推移人们会发现新的属性值.这非常符合人类对开放世界的认知.正是因为这个可以不是满射的性质，我们就可以借助于它来刻画开放世界.

这就是刻画开放系统的模型具有的另一个本质属性：

性质2 给定开放世界信息系统的模型序列MS={Mi|i∈} ，那么这些模型必然满足下列开放信息系统条件:对于任给的开放类属性a，对于任给的M′, M∈MS，若M′≥ M，则(VCa)M′⊇ (VCa)M.

在认识世界的时候随着时间的推移人们会发现新的属性值，也会发现新的属性，本文对该特性已给出了描述，因为假定属性a在当前模型下没被发现认识到，该属性和任意的论域个体都没给定像，即是说f此时的模型下只是个部分映射.本文引入未知属性值符号和若干个属性值符号va,这些属性值可能在以后的模型世界中能被认知.当前模型下的f,只要将(x,a)映成即可，于是就将部分映射扩展成映射.这样我们就描述了特性——在认识世界的时候随着时间的推移人们会发现新的属性.

2.3 公理及推理规则

2.3.1 公理

(1)信息公理

A1.命题公理中的3条公理;

A2.(a,v)→(a,v′),对所有的v≠v′;

A3.∨v∈VCa(a,v),对所有的a∈AC;

(2)更新公理

A4.[I]p↔p;

A5.[I]α↔[I]α;

A6.[I](α→β)↔ ([I]α→[I]β);

A7.[(φ,a,v)](a′,v′)↔ (a′,v′),当a≠a′;

A8.[(φ,a,v)](a,v′)↔ (φ∧(a,v′)),当v≠v′;

A9.[(φ,a,v)](a,v)↔ (φ→(a,v));

A10.[σ;σ′]α↔ [σ][σ′]α;

A11.[σ∨σ′]α↔ ([σ]α∧[σ′]α);

(3)开放世界公理

A13.(a,v)→[I](a,v),当a∈B∪C∪D;

2.3.2 推理规则

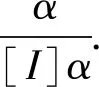
2.4 形式证明

例1 证明[I](α∧β)↔ ([I]α∧ [I]β).

证(1) [I]((α∧β)↔[I](α∨β)(命题逻辑推理,RE规则).

(2) [I](α∨β) ↔[I](α∨β) )(A5).

(6)([I]α∧[I]β)↔([I]α∧ [I]β) (命题逻辑推理).

(7)[I](α∧β)↔([I]α∧ [I]β)((1)-(6),命题逻辑推理).

例2 证明Pi→[I1;I2;...;In]Pi，这里Pi=∧b∈Bi(b,vb)∧ ∧c∈CBi(c,vc′).

证以n=2为例给出证明，一般情形同理可证.

(1) (b,vb)→[I2](b,vb) (A13),

(2) [I1]((b,vb)→[I2](b,vb)) ((1),RN),

(3) [I1]((b,vb)→[I2](b,vb))→([I1](b,vb)→[I1][I2](b,vb)) (A6),

(4) [I1](b,vb)→[I1][I2](b,vb)((2),(3),MP),

(5) (b,vb)→[I1](b,vb) (A13),

(6) (b,vb)→[I1][I2](b,vb)((5),(4),命题逻辑的定理),

(7) (b′,vb′)→[I1][I2](b′,vb′) (与(6)同理),

(8) ((b,vb)∧ (b′,vb′))→([I1][I2](b,vb)∧[I1][I2](b′,vb′))((6),(7),命题逻辑的定理),

(9)([I2](b,vb)∧ [I2](b′,vb′))→[I2]((b,vb)∧ (b′,vb′)) (例1),

(10)[I1](([I2](b,vb)∧[I2](b′,vb′))→[I1][I2]((b,vb)∧ (b′,vb′))) ((9),RM规则),

(11)([I1][I2](b,vb)∧[I1][I2](b′,vb′))→[I1]([I2](b,vb)∧ [I2](b′,vb′)) (例1),

(12)((b,vb)∧(b′,vb′))→[I1][I2]((b,vb)∧ (b′,vb′)) ((8),(11),(10),命题逻辑推理),

(13)(∧b∈Bi(b,vb))→[I1][I2](∧b∈Bi(b,vb)) (重复(12)的证明若干次),

(14)(∧b∈Bi(b,vb)∧∧c∈CBi(c,vc′))→[I1][I2](∧b∈Bi(b,vb)∧ ∧c∈CBi(c,vc′)) (再重复(12)的证明若干次).

Pi→[I1;I2;…;In]Pi直观解释为：随着信息的更新，开放世界中的开放类成员可能会增加.这也正是开放系统的模型具有的一个本质属性.

下面给出开放世界公理的直观解释，这非常有助于理解下一节的可靠性定理的证明过程.

A13.(a,v)→[I](a,v),当a∈B∪C∪D直观解释为：更新一次信息，开放世界中的开放类成员可能会增加.这为开放系统的模型的本质属性提供基础保证.

3 开放世界信息更新的逻辑系统的可靠性

KHAN等[8]给出了信息系统及其动态更新系统的可靠性，本节来证明开放世界信息系统更新的逻辑系统的可靠性.

引理1 每一条公理都是有效的.

证明选证公理A2、A6、A13和A15的有效性，其余的公理同样能证明(A1—A11和文献[8]中的公理一样，他们已经证明信息系统及其更新系统具有可靠性，所以略去的其中的大部分公理的有效性的证明，只是着重给出开放公理的有效性的证明).

A2.(a,v)→(a,v′),对所有的v≠v′;任给模型M及任意的w∈W，若有w∈(a,v)M，而因v≠v′得于是有w∈((a,v))M.由公式的可满足性的定义有w∈((a,v)→(a,v′))M.由有效性的定义得A2有效.

A6.[I](α→β)↔([I]α→[I]β);任给模型M及任意的w∈W，要证得w∈(A6)M，即要证2个命题:(1)若w∈([I](α→β))M则w∈([I]α→[I]β)M；(2)若w∈([I]α→[I]β)M则w∈([I](α→β))M.

(1)若w∈([I](α→β))M，即是MI,wα→β.设M,w[I]α即是MI,wα，结合MI,wα→β，于是有MI,wβ.这即是M,w[I]β.故w∈([I]α→[I]β)M.

(2)若w∈([I]α→[I]β)M，即是说若w∈([I]α)M则w∈([I]β)M.于是若w∈αMI则w∈βMI.即是w∈(α→β)MI，所以w∈([I](α→β))M.

A13.(a,v)→[I](a,v),当a∈B∪C∪D;任给模型M及任意的w∈W，要证得w∈(A13)M，即要证命题:若w∈(a,v)M则w∈([I](a,v))M.下面就I的可能情况讨论：

(1)当I=(φ,a,v)时，再就w是否属于φM来讨论.(1.1) 当w∉φM时，因为已经设有w∈(a,v)M，即是M,w(a,v)，再因w∉φM于是MI,w(a,v)，这就有w∈(a,v)MI即w∈([I](a,v))M；(1.2)当w∈φM时，(1.2.1)信息I与信息系统SM相容，由相容的定义有若w∈φM都有f(w,a) =.因f(w,a)=，信息I=(φ,a,v)就是要得到fI(w,a)=v，于是有w∈((a,v))MI即w∈([I](a,v))M；(1.2.2)信息I与信息系统SM不相容，因为已经设有w∈(a,v)M，即是M,w(a,v)，于是MI,w(a,v)，这就有w∈(a,v)MI即w∈([I](a,v))M；

(2)当I=(φ,a,v′)时，(2.1)信息I与信息系统SM相容，由信息I与信息系统SM相容的定义得若w∈φM，则f(w,a)=，这与已设w∈(a,v)M(即是说f(w,a)=v))矛盾，于是w∉φM，由定义知集合 (a,v)MI先从(a,v)M要去掉像值为v的w这样的元素，再加上信息给带来的那些φM中的元素，于是显然有w∈(a,v)MI即w∈([I](a,v))M；(2.2)信息I与信息系统SM不相容，因为已经设有w∈(a,v)M，即是M,w(a,v)，于是MI,w(a,v)，这就有w∈(a,v)MI即w∈([I](a,v))M；

(3)当I=(φ,b,vb),b≠a时，因为已经设有w∈(a,v)M，即是M,w(a,v)，于是MI,w(a,v)，这就有w∈(a,v)MI即w∈([I](a,v))M.

综上所述，故A13有效.

A15.[(Pi*,c1,vc1″);(Pi*,c2,vc2″);...;(Pi*,ck,vck″)]Pi-→(Pi-∨(Pi*∧ ∧c∈CBi(c,))).任给模型M及任意的w∈W，要证得w∈(A15)M，即要证命题:

引理2 每一规则都保持有效性.

证明MP规则保持有效性的证明：任给模型M及任意的w∈W，因α,α→β都是有效的，故w∈αM，w∈(α→β)M,于是w∈βM.由有效性的定义得β是有效的,因此MP规则保持有效性.

RI规则保持有效性的证明：任给模型M及任意的w∈W，因α是有效的，MI也是一个模型，故w∈αMI，由MI的定义即得w∈([I]α)M，由有效性的定义得[I]α是有效的，因此RI规则保持有效性.

由引理1和引理2即得可靠性定理.

4 结束语

本文通过剖析开放系统的模型的本质属性，表明这样给出的系统中存在真正的开放类.通过扩展一般的信息系统中的信息表这个映射，将信息系统拓展到开放信息系统上,从而结合开放类和信息系统建立了开放世界信息更新的逻辑系统.

逻辑研究学者们总希望得到能够描述具体实例世界的形式系统.从分析具体的开放类的实例——SARS入手，上升到理论深度，再通过将信息系统的信息表映射推广到一般的非满映射上来，进一步给出开放类的逻辑系统的刻画.这无论是从现实的需要还是纯理论的推广中都得出建立开放世界信息更新的逻辑系统是必要的.结合PAWLAK等提出的粗糙集逻辑和鞠实儿提出的开放类，给出开放世界信息更新的逻辑系统，它刻画了开放世界信息系统的动态更新.KHAN和BANERJEE在文献[9]给出多主体信息系统更新的逻辑系统.接下来进一步的工作可以将单主体的开放世界信息系统的更新推广到多主体的情形，这将是有意义和令人鼓舞的事情.