类分形修饰法研究活性炭对孔雀石绿的吸附动力学

韩传喜,高 原,徐世艾,冯咏梅,殷国俊

(1.烟台大学化学工程与过程山东省重点实验室,山东 烟台 264009;2.北京理化分析测试中心,北京 100089)

吸附技术广泛应用于化工生产中,如气体分离和废水处理等过程[1]．研究吸附动力学可以确定吸附时间、解释吸附机理和获得平衡吸附量,对于指导吸附装置的设计和操作非常重要,因此研究吸附动力学具有一定的理论价值和实际需求．

前人在吸附动力学研究上取得了很多重要进展,常用的动力学方程包括准一级动力学方程(PFO)和准二级动力学方程(PSO)．LAGERGREN于1898年根据草酸和丙二酸在木炭上的吸附过程提出了PFO[2],如方程(1)所示:

qt=qe[1-exp(-k1t)],

(1)

式中,qe和qt分别代表平衡时间和任一时刻t时的吸附量,k1为吸附速率常数．

HO等提出了以(qe-qt)为驱动力的PSO[3],如方程(2)所示:

(2)

式中,k2为PSO的吸附速率常数．

作为经典动力学方程,方程(1)、(2)被广泛应用于吸附过程的研究．需要注意的是,它们都是基于理想状态的纯理论方程,因而在分析实际吸附过程中不可避免地会出现偏差,对实验数据拟合度较低,从而影响吸附动力学机理的判别和相关参数的获取．为了降低经典动力学方程在使用过程中的偏差,近年来有许多学者引入类分形法来修饰吸附动力学方程[4-7]．类分形法的理论依据是MANDELBROT提出的分形学,可解释不规则、分散的物体,它们没有特征长度的图形与构造[8]．显然,吸附材料具备这些特点,因此可以借鉴该理论来研究吸附过程．

用活性炭从染料废水中脱除孔雀石绿是环境领域的研究热点[9],但对该过程的吸附动力学行为还没有形成共识．本文拟深入研究孔雀石绿在活性炭上的吸附动力学,分析3种不同材质的活性炭(杏核炭、煤质炭和椰壳炭)在25～45 ℃下对孔雀石绿的吸附行为,利用经典动力学方法和类分形修饰法进行对比分析,获取关键参数的变化规律,从而凝练出活性炭对孔雀石绿吸附动力学的有效分析方法．

1 理论部分

1967年,MANDELBROT依据统计自相似性原理,首次提出分形原理用于描述形状不规则的物体[8, 10]．KOPELMAN将分形原理用于研究分子激发-聚变反应,归纳出了反应速率常数与时间的关系,可用方程(3)表示[11]:

k=k0t-h,

(3)

式中,k为反应速率常数,k0为与时间t无关的常数,h是谱维数.AO理论给出了h的计算式,如方程(4)所示[12]:

(4)

式中,df为分形体的分形维数,dw为分形体的行走维数．

AZIZIAN等借鉴分形原理来分析吸附过程,如图1所示[12]．假设吸附质分子在不同吸附时间到达吸附剂表面的路径不同,在时间为t1时,吸附剂表面的活性位点没有吸附质被吸附,此时吸附质沿着(a)路径运动到活性位点;当吸附时间延长到t2时,部分活性位点被吸附质占据,未被吸附的吸附质沿着(b)路径运动到活性位点;当吸附时间继续延长到t3时,大部分活性位点被吸附质占据,未被吸附的吸附质沿着(c)路径运动到活性位点．

上述过程与KOPELMAN的分子激发-聚变反应过程类似,但这2个过程所代表的物理意义是完全不同的．为了区别于KOPELMAN的方程,吸附速率常数与时间的关系用方程(5)表示,AZIZIAN等将其称为类分形方法修饰吸附速率系数方程:

k′=k0′t-h′,

(5)

式中,k′为吸附速率常数;k0′为与时间t无关的常数;h′是谱维数．

将方程(5)代入方程(1),得到类分形修饰准一级方程(FL-PFO):

q=qe[1-exp(-k1′tα)].

(6)

将方程(5)代入方程(2),得到类分形修饰准二级方程(FL-PSO):

(7)

2 实验部分

称取0.05 g样品(分别为杏核炭、煤质炭和椰壳炭,20～40目,烟台通用活性炭厂)与25 mL初始浓度为200 mg/L的孔雀石绿溶液混合,置于恒温摇床中(25、35和45 ℃),在160 r/min的转速下进行混合吸附,每间隔一段时间测定溶液中孔雀石绿浓度,直到吸附平衡[9]．

3 结果与讨论

3.1 准一级和准二级动力学分析

为了对比类分形修饰前后吸附动力学方程对实验数据的拟合度,首先用PFO和PSO方程来分析吸附量随时间的变化,如图2,3,4所示．表1列出了2个方程对实验数据的拟合参数．从中可以看出,对于PFO和PSO来说,两者的决定系数R2相近,但从其他衡量拟合度的参数残差平方和(SSE)、卡方系数(χ2)来看,PFO的拟合效果更好,并且计算得到的理论平衡吸附量较接近实验测定的平衡吸附值．

3.2 类分形修饰动力学方程分析

用FL-PFO和FL-PSO对吸附数据进行拟合,如图3所示．表2列出了这2组方程对实验数据的拟合参数．与经典动力学分析相比,类分形修饰法可以更好地拟合实验数据,并且计算所得的理论平衡吸附量也更加接近于实际吸附量．

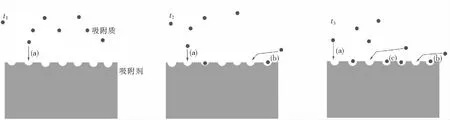
图1 吸附路径示意图[12]

图2 孔雀石绿在杏核炭的吸附行为

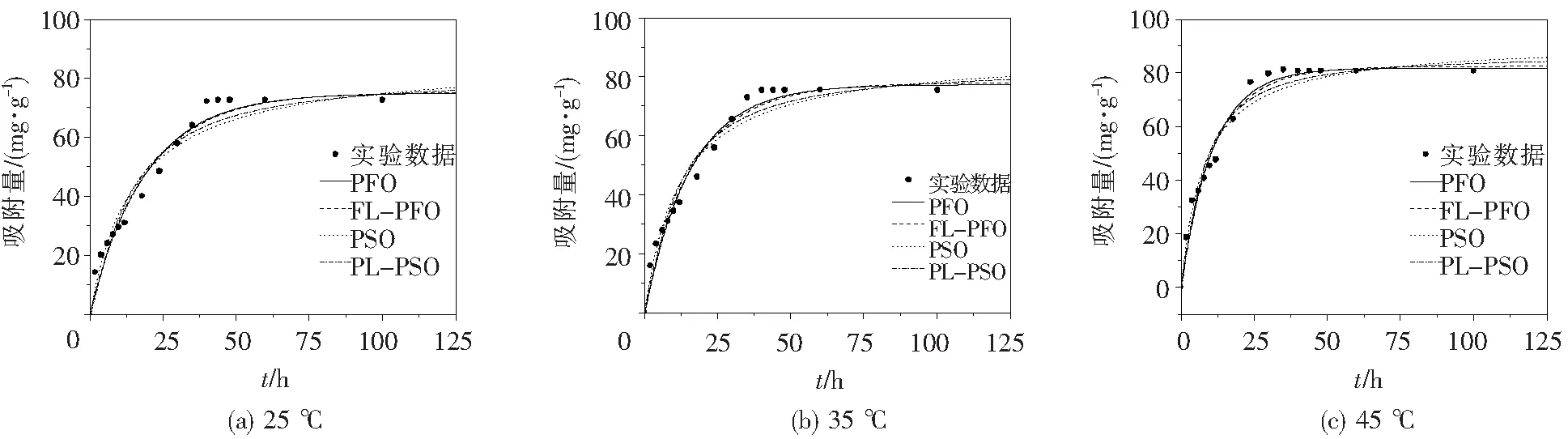
图3 孔雀石绿在煤质炭的吸附行为

图4 孔雀石绿在椰壳炭的吸附行为

由拟合参数可以看出,类分形方程中的R2相比经典动力学方程有了小幅度的提高;SSE出现了明显的下降,平均下降了65,说明类分形动力学方程可以更好的描述炭材料吸附孔雀石绿的过程．而在两个类分形动力学方程中,FL-PFO相比FL-PSO具有更高的决定系数和更低的残差平方和,且由FL-PFO所计算得出的平衡实验值更接近实际平衡值,误差在2.5%左右．

3.3 类分形修饰法中关键参数的分析

从用类分形修饰前后的方程可以看出,类分形修饰后动力学方程中增加了α指数．从表2可以看出,对于FL-PFO,3种活性炭的α值随温度的升高呈减少的趋势;对于FL-PSO,杏壳炭和椰壳炭的α值随温度的升高呈减少的趋势,而煤制炭的α值随温度升高,先增大后减少．由α值的表达方式可知,df为分形体的分形维数,是描述分形结构的几何参量,与分形体的不均匀性有关;dw为描述分形体的行走维数,是描述分形结构中扩散动力学的参量[13-14]．随着温度的升高,分子的热运动逐渐变的剧烈,引起dw增大导致α减小．这说明FL-PFO不仅对全部实验数据的拟合度最高,而且符合物理学意义．

表1 PFO与PSO动力学方程的拟合参数

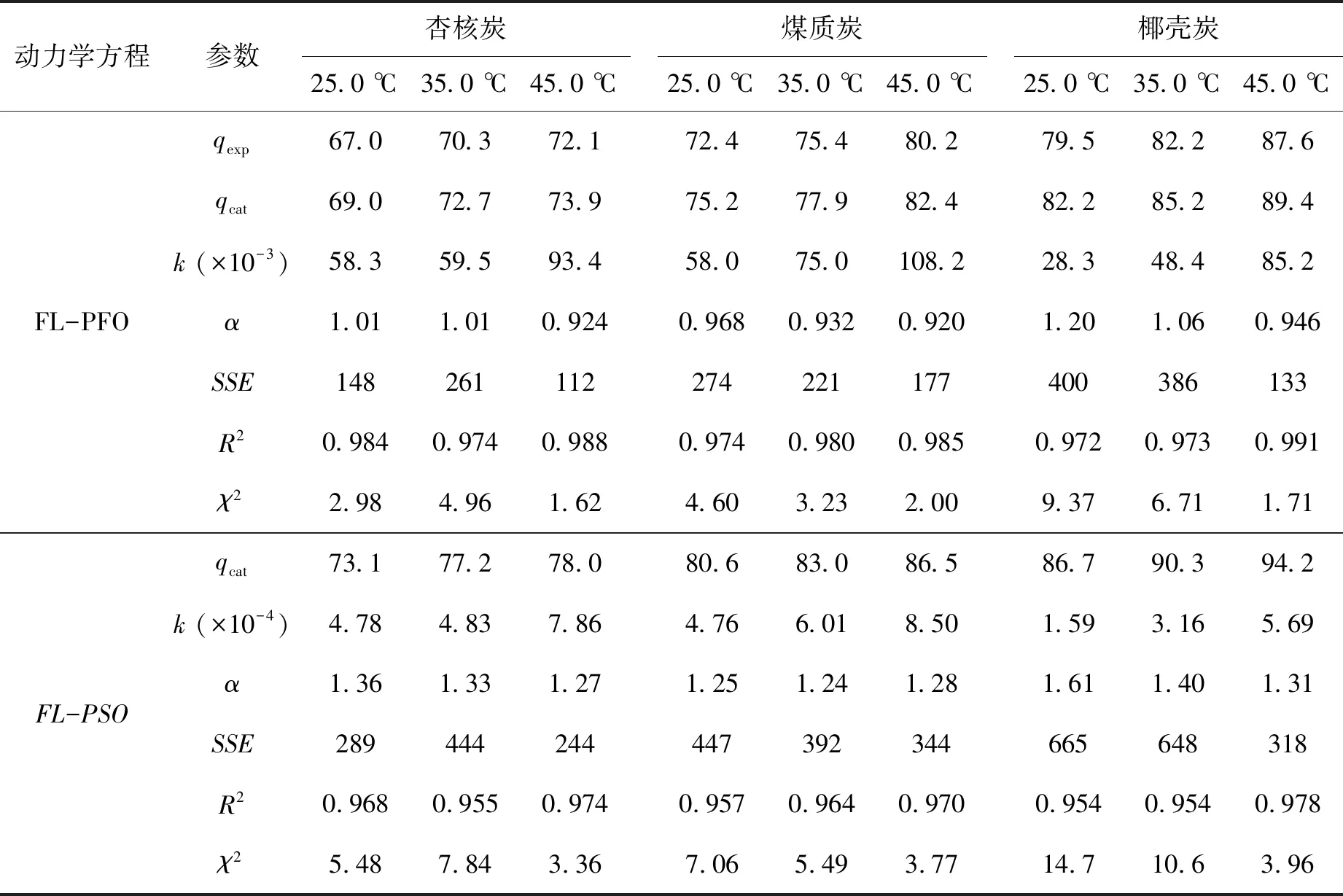
表2 FL-PFO 与FL-PSO动力学方程的拟合参数

4 结 论

本文研究了在25～45 ℃下,3种商业活性炭对孔雀石绿的吸附动力学,获得如下结论:类分形修饰法可以提高传统准一级和准二级动力学方程对实验数据的拟合度,这说明类分形修饰法用于动力学研究具有独特优势;与准二级动力学方程相比,类分形修饰后的准一级动力学方程可以较好地拟合孔雀石绿在活性炭上的吸附行为;随着吸附温度的上升,吸附质分子的热运动加剧引起了行走维数的增大,导致类分形修饰法的关键参数α值呈下降趋势．