科利法在教育测量中的应用

郭东威,丁根宏

(1. 周口师范学院数学与统计学院,河南 周口 466000;2. 河海大学理学院,江苏 南京 211100)

在教育测量中,有一些测验难以用客观的方法打分,往往会受到评分者主观因素的影响而产生较大误差,比如对竞赛论文、作文及艺术作品等的评分.评分误差从广义上可以分为系统误差、随机误差和人为误差.系统误差是指由评分者评分风格引起的恒定有规律的偏差,总是以一定的大小和方向偏离真分数.例如,有的评分者非常严格,评分普遍偏低;有的评分者较为宽松,评分普遍偏高;有的评分者的评分区分度较大,而有的评分者的评分区分度较小.随机误差是指由评分者不确定因素引起的无规律的偏差,评分大小和方向均是完全随机地偏离真分数.人为误差是指评分者有意提高或降低评分.从信度的角度来说,系统误差对评分者之间的信度影响较小,也就是对被试的等级影响不大,但是会造成评分不准确,不能客观反应被试的水平;随机误差和人为误差对评分者之间的信度一般影响较大,容易造成评分的不一致.为了公平评判被试的水平,通常由多个评分者对被试进行评分.如果每个被试都有相同的评分者进行评分,也就是评分矩阵是完整的,并且评分者之间的信度较高,那么可以用传统法(直接取均分法)作为被试的终评成绩.这样的终评成绩虽然存在误差,但是依据分值大小化为等级,可以较好地反应被试者在被试群体中的相对水平.在大型竞赛或考试中,受多种客观因素的制约,如被试人数众多、评分者数量有限、评阅时间限制等,上述理想的评阅方案一般行不通,通常是每个被试随机分配给几个评分者进行评分,也就是说评分矩阵是残缺不全的.在这种情况下,即使评分者之间的信度很高,也不易直接对原始评分取均值作为被试的终评成绩,因为这样的终评成绩由于系统误差的影响既不能很好地反映被试的客观水平,也不能科学地反映被试的相对水平(等级).

国内外应用多种方法对主观型评分做了大量的研究.1993年WIGGLESWORTH[1]的研究表明评分者之间的变异是测量误差的主要来源之一.尽管评分者经过培训并遵守评分量表的规则,但是不同的评分者对同一被试的评分依然不一致,甚至有时差异很大[2-3].在经典测量理论(CTT)的基础上发展起来了概化理论(GT),该理论通过方差分析等技术,从多个侧面进行量化分析来估计不同误差对测量分数的影响[4-6].2002年我国学者严芳等[7]介绍了用结构方程模型来估计概化理论中的评分者信度.Rasch模型是项目反应理论的基本模型之一,田青源[8]、王跃武等[9]应用Rasch模型研究了主观评分中评分者的信度.陈菊咏[10]、马春燕[11]分别利用LONGFORD方法对评分者信度及异常分数进行了研究.此外,还有其他一些方法,可以参看文献[12-15].

本文主要研究系统误差、人为误差及评委误判在残缺评分型竞赛中的影响.如作文竞赛、大学生数学建模竞赛等,这类大型竞赛不仅重视成绩(分数),以测验被试的绝对水平,而且还很看重等级(名次),用来评出获奖者.为了较好地测量被试的客观水平,本研究采用体育竞技排名方法科利法对被试进行评价.实例分析表明,该方法对被试进行评价具有无偏性及较好的稳定性.所谓无偏性是指被试的终评成绩(或等级)仅与各评分者对被试的排名有关,不受原始评分系统误差的影响.稳定性是指当某一个或几个原始分数出现异常时,不至于导致终评等级严重偏离客观情况.稳定性好的评判方法,能够有效减小人为误差及评委误判造成的不公平,尽可能保证评判结果的科学性.

1 评分者信度的计算方法

评分者信度是度量带有主观判断成分的测量可靠与否的重要指标,包括评分者内信度(intra-rater reliability)和评分者间信度(inter-rater reliability).评分者内信度是指单个评分者对同一组被试的答卷进行两次评分的一致性程度[16].考察评分者内信度通常需要同一评分者对答卷先进行一次评分,然后间隔一定时间后以随机顺序对其重新评分,两组评分之间的相关系数即为评分者内信度.评分者间信度是指多个评分者对同一批被试的答卷进行评分的一致性程度[3].本文主要应用评分者间信度进行分析,信度越高表示评分者对被试的评判越一致.

1.1 积差相关法

如果被试答卷是由两位评分者按照各自的评分标准进行评分,则评分者间信度可以用每份答卷的2个分数之间的积差相关系数来表示.一般要求在成对的受过训练的评分者之间平均相关系数达到0.90以上,才认为评分是客观的[3].假设A、B 2个评分者对n份答卷进行评分,评分向量分别为X=(x1,x2,…,xn)和Y=(y1,y2,…,yn),xi和yi分别表示评分者A和B对i答卷的评分,那么积差相关系数的计算公式可表示为

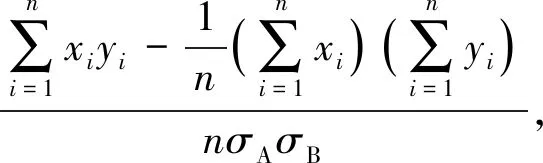
(1)

由于积差相关系数不具有等距单位,因此不能直接进行加减算术运算.若需要将测量中几部分的积差相关系数综合成一个总的系数来表示多个评分者间的整体信度时,可以用统计学家费舍(Fisher)的Zr转换法,转换公式为

(2)

然后求出Zr的均值,最后再利用式(2)的反函数求出多个评分者间的整体信度.

使用积差相关法要满足以下几个条件:评分是连续性数据;每个评分者的评分总体服从正态分布或接近正态分布,至少是单峰对称的分布;评分者的评分相互独立;两组分数之间呈线性关系;被试数量不少于30.

1.2 等级相关法

等级相关是指评分者对答卷以等级的方式进行评判时,各评判等级次序之间的相关.根据评分者多少可以分为斯皮尔曼(Spearman)二列等级相关及肯德尔和谐系数(the Kendall’s coefficient of concordance)多列等级相关.

1.2.1 斯皮尔曼等级相关 斯皮尔曼等级相关适用于度量2个评分者以等级方式评判同一组答卷的一致性程度.计算斯皮尔曼等级相关系数时不要求评判等级呈正态分布,也不要求被试数量大于等于30,相对积差相关要求较低,因此使用范围较广.计算斯皮尔曼等级相关系数的公式为

(3)

其中,rtt表示2个评分者之间的信度系数(等级相关系数);Di表示i答卷的2个等级之差;n表示被试人数.

1.2.2 肯德尔和谐系数 当有2个以上评分者以等级方式对同一组被试进行评判时,表示评分者评判等级之间的一致性程度的量称为肯德尔和谐系数(评分者间信度).

单个评分者对所有被试的评判没有相同等级时,肯德尔和谐系数计算公式为

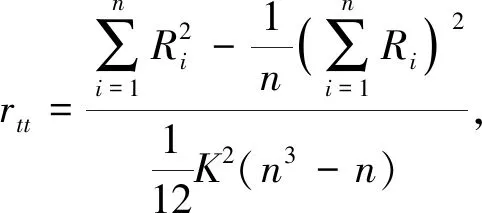
(4)

其中,rtt表示评分者之间的信度系数(肯德尔和谐系数);K表示评分者人数;Ri表示K个评分者对i答卷评判的等级之和;n表示被试人数.

当单个评分者对所有被试的评判有相同等级时,肯德尔和谐系数计算公式可校正为

(5)

其中,m表示相同等级的个数,其余变量的含义与式(4)中相同.

1.3 克龙巴赫α系数法

当K(K≥3)个评分者以连续性评分的方式对同一组n个被试进行评判时,评分者间的信度可以用克龙巴赫α系数来估计,计算公式为

(6)

2 科利法在教育测量中的应用

为了克服胜率法的缺陷,WESLEY COLLEY根据拉普拉斯的“继承法则”(rule of succession)对其进行了改进,即

(7)

假设上式为一等式,代入式(7),得

或写为

(8)

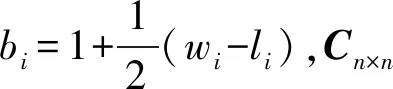
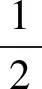
根据科利评分ri的大小可以确定各被试的等级.由于科利评分ri∈(0,1),不符合人们习惯的百分制表示法,不过可以用多种方法把它转化为百分制分数.比如:

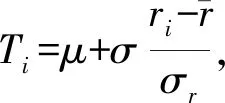
(3)由于科利评分ri∈(0,1),因此最简单的方法可以直接用100乘以科利分.

利用科利法对被试进行等级排名是无偏的,即评判的结果仅利用被试与被试在直接比较情况下的优劣(等级)信息,而不直接利用原始评分.无偏性在一定程度上增强了评判结果的稳定性,即当被试由多个评分者评判,出现个别异常分数时,由于不直接利用原始分数做最终的评判,减小了原始分数对终评的影响,使得终评等级不会出现较大偏差,在下一节“实例分析及比较”中可以明显看出“稳定性”的效果.

3 实例分析及比较

本节以H高校大学生数学建模竞赛为例来说明科利法的有效性.竞赛论文30篇,评分者5人.为了实验的可靠性,30篇论文的主题(问题)完全一样,选择的5位评分者均为外校教授或副教授职称,并多次参加全国大学生数学建模竞赛的评阅工作,具有丰富的阅卷经验.5位评分者均收到这30篇论文及完全一样的评分标准,且论文上没有作者信息只有编号,按百分制评分.各评分者原始评分及对应等级见表1.

表1 原始评分及对应等级

被试个数n=30,可以用Shapiro-Wilk检验(W检验)来检验各评分者的评分是否服从正态分布,检验结果见表2.结果表明5位评分者的评分在显著性水平0.10下均服从正态分布.

表2 Shapiro-Wilk检验结果

5位评分者评分的均值及标准差见表3.

表3 评分均值及标准差

用Hartley检验法对5位评分者的评分进行方差齐性检验,计算结果为

3.474 4>H1-0.05(5,29)≈2.78,

即在显著性水平α=0.05下,认为5位评分者的评分方差有显著差异.由于方差有显著差异,因此无法用方差分析来检验均值是否有显著差异,但是从表3可以看出,5位评分者评分均值的极差为7.34,说明本次的评分存在一定的系统误差,其中评委2和4均分较大,评委1、3、5均分较小,评委1和3方差较大,而评分者2和4的方差较小.

由表1中的数据用3种方法计算评分者信度,结果见表4.

3种方法计算结果均在0.95以上,说明评分者信度较高,评判结果具有较高的一致性.

表4 评分者信度

基于以上对评分者评分的均值、方差及信度的分析,可以认为论文的等级由标准分(Z分数)法来确定是比较科学的,具有较强的可信度.为方便表述,称之为“标准等级”.事实上,由传统法(取原始评分均值)排名与按照标准分均值排名的结果仅有稍微差别,见表5,表中斜体加黑标出的即为有差异的结果.

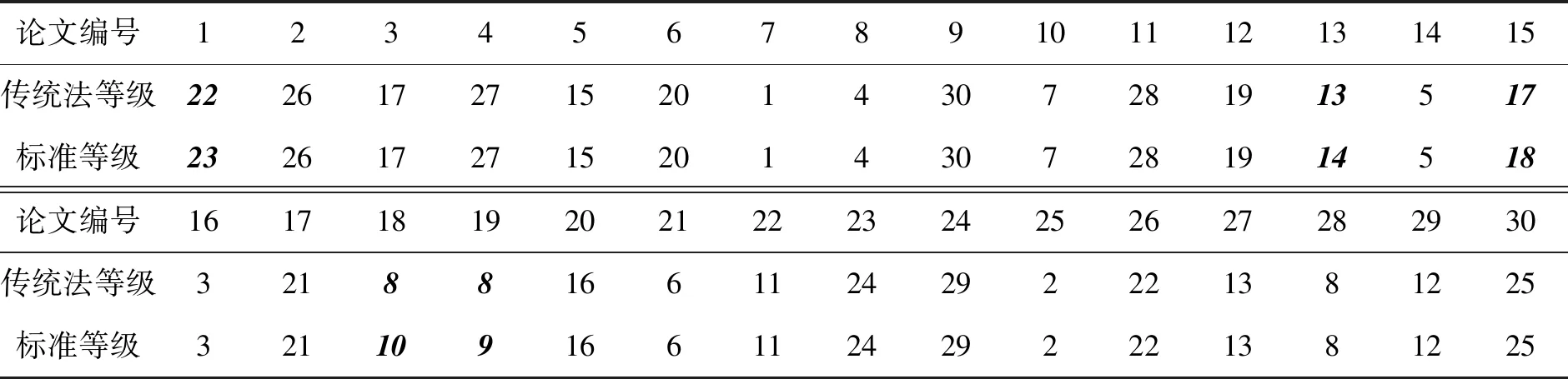
表5 传统法与标准分法等级比较

从表5中可以看出传统法容易出现等级相同的现象,例如论文18、19、28的等级排名均为8.

下面以实验来分析系统误差、随机误差及人为误差对残缺型评分的影响.首先将表1中每篇论文随机去掉2个分数,但是最终要保证每个评分者都评阅18篇论文,结果见表6.

表6 残缺评分表

下面分两类实验来比较不同评判方法结果的稳定性.第一类是纵向实验:随机选择一个评分进行不同变异(相当于评分者评分时误判、故意提高或降低分数),然后根据传统法、标准分法及科利法分别确定被试等级,并与表5中的“标准等级”进行比较,计算斯皮尔曼等级相关系数.记符号xij表示评委j对论文i的评分.不妨选择评分x13,3做实验,依次将x13,3=71变异为60、65、75、80、85、90.计算斯皮尔曼等级相关系数,结果见表7.

表7 斯皮尔曼等级相关系数

相关系数.

第二类是横向实验:随机选择个别评分进行变异.进行5组实验,变异情况分别为:变异1:x12,1=69→86,x21,4=81→70;变异2:x8,5=81→70,x18,3=82→65;变异3:x7,3=95→80;变异4:x24,4=64→75;变异5:x18,3=76→60,x23,3=60→80.3种评判方法的结果与“标准等级”比较的斯皮尔曼等级相关系数见表8.

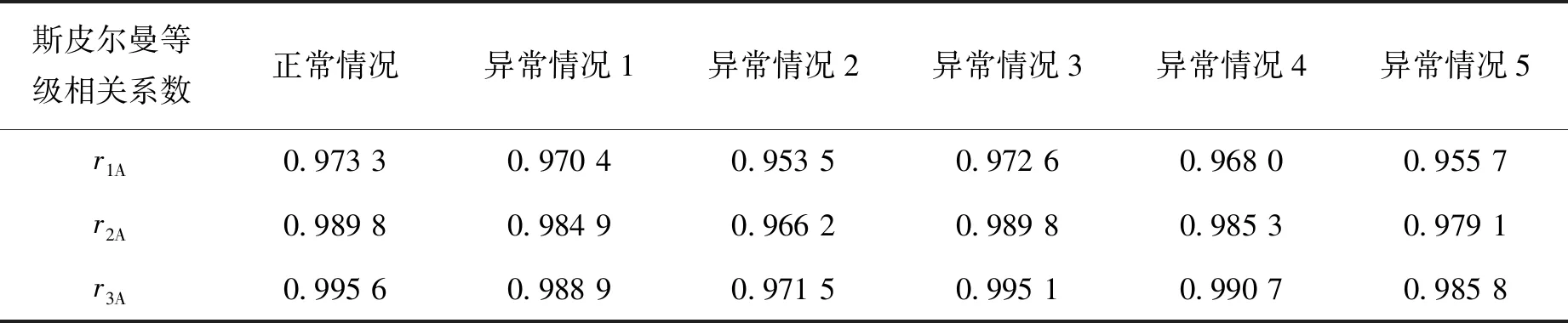
表8 斯皮尔曼等级相关系数

由表7及表8斯皮尔曼等级相关系数可知,由于评分误差的存在,3种评判方法的结果与“标准等级”均有差异,尤其是传统方法评判的结果偏差最大.无论是在正常情况下还是变异之后,由r2A>r1A说明在残缺评分情况下系统误差会给传统方法的评判结果带来较大偏差,由r3A>r2A>r1A说明科利法的评判结果要比传统法及标准分法更客观合理.2个表中r3A分别均在0.99及0.98以上,说明科利法较传统法及标准分法更稳定,即当个别分数出现异常时,依然可以得出较客观的评判结果.

4 结束语

在残缺型主观评分测量中,传统法及标准分法的评判结果受评分误差影响较大,尤其是传统法.科利法的评判结果是无偏的,它仅用到被试与被试之间直接比较的等级信息,而不直接利用原始评分,因此降低了系统误差及个别异常分数对评判结果的影响,具有较好的稳定性.