考虑主管轴压比影响的T型管节点抗冲击承载力研究

李亚锦,曲 慧,陈 琦,董 波

(1.烟台大学土木工程学院,山东 烟台264005;2.山东岩土勘测设计研究院有限公司,山东 烟台264000)

钢管凭借其轻质、高强、造价低的特点被广泛应用于海洋平台和大跨结构中．钢管节点在冲击荷载的作用下,易发生局部凹陷或杆件节点破坏,进而造成结构的整体失效甚至倒塌,研究钢管节点在冲击荷载作用下的抗冲击性能对结构的防灾减灾具有重要意义．

国内外学者对管节点的抗冲击性能做了深入分析．ZEINODDINI等[1-2]运用ABAQUS建立了预加轴力下、一端固定、一端可水平滑动的薄壁圆钢管冲击模型,并进行了侧向冲击试验,通过对模型参数、冲击力和位移时程曲线进行分析,推导出冲击破坏后钢管的破坏模态和冲击力与管节点变形之间的关系、锤头与钢管之间的界面接触力等．曲慧等[3-4]采用有限元软件ABAQUS建立了冲击荷载下的T型管节点模型,并基于能量的塑性铰线理论,提出了等效冲击承载力简化评估方法．KHEDMATI和NAZARI[5]通过数值模拟分析了钢管在不同预加轴力和边界条件下的抗冲击性能,结果表明预加轴力会降低钢管的极限强度．陈高哲[6]和欧阳翊龙[7]对多个预加不同轴力的管节点进行有限元模拟和落锤冲击试验,并对侧向冲击下方钢管节点的破坏模态和冲击力进行了全面分析,计算了节点在动力荷载下的承载力．GAO等[8]通过落锤试验和有限元模拟,分析了落锤的冲击力、位移和能量耗散与落锤的冲击能量之间的关系,并明确冲击持续时间与冲击动量直接相关．

T型管节点的抗冲击承载力是判断管结构抗冲击性能的一个重要指标,相关学者提出了多种管节点承载力的判断方法．比如,LU等[9]在研究管节点承载力时,以主管局部变形为3%D(D为主管直径)时的承载力作为节点的极限承载力;《建筑抗震设计规范》(GB5011—2010)[10]中以主管整体变形上限(L/2)/50所对应的承载力作为节点的极限承载力；YOUSUF等[11]提出一种简便的评估钢管抗冲击承载力的方法,即以冲击力时程曲线的水平段来确定节点极限承载力．

在实际工程中,钢管作为轴向受力构件,遭受冲击荷载时,不同轴压比对钢管的破坏模态和承载力有较大影响．因此,研究不同轴压比下钢管节点的抗冲击性能对保证钢管结构的安全性具有重要意义．叶卉[12]对预加轴力作用下的T型管节点进行了侧向冲击试验,结果表明轴压力会加大主管的局部和整体变形．但由于试验条件的限制,仅设置了轴压比为0和0.3的2组试验,不能充分表现出轴压比对T型管节点抗冲击性能的影响．本文根据叶卉[12]在T型管节点模型和试件,运用ABAQUS建立了冲击荷载下的T型管节点模型,通过对数值模拟结果与叶卉[12]试验结果比较,验证本文有限元模型的准确性．在此基础上,对轴压比分别为0、0.3、0.6、0.9的T型钢管节点进行抗冲击性能有限元数值模拟研究,通过分析节点的破坏模态、抗冲击承载力、局部和整体变形,揭示了侧向冲击时不同轴压比对未加强管节点抗冲击性能的影响．

1 有限元模型

1.1 典型节点模型

依据《钢结构设计标准》(GB50017—2017)[13]中对管节点几何参数的规定,并选取叶卉[12]一文中侧向冲击的T型管节点作为典型分析模型,运用有限元软件ABAQUS建立T型管节点有限元模型,如图1所示．T型管节点的几何尺寸和荷载参数如表1所示．其中,主管直径、壁厚、长度分别以D、T、L表示;支管直径、壁厚、长度分别以d、t、l表示．主管的轴压比分别设置为0、0.3、0.6、0.9．

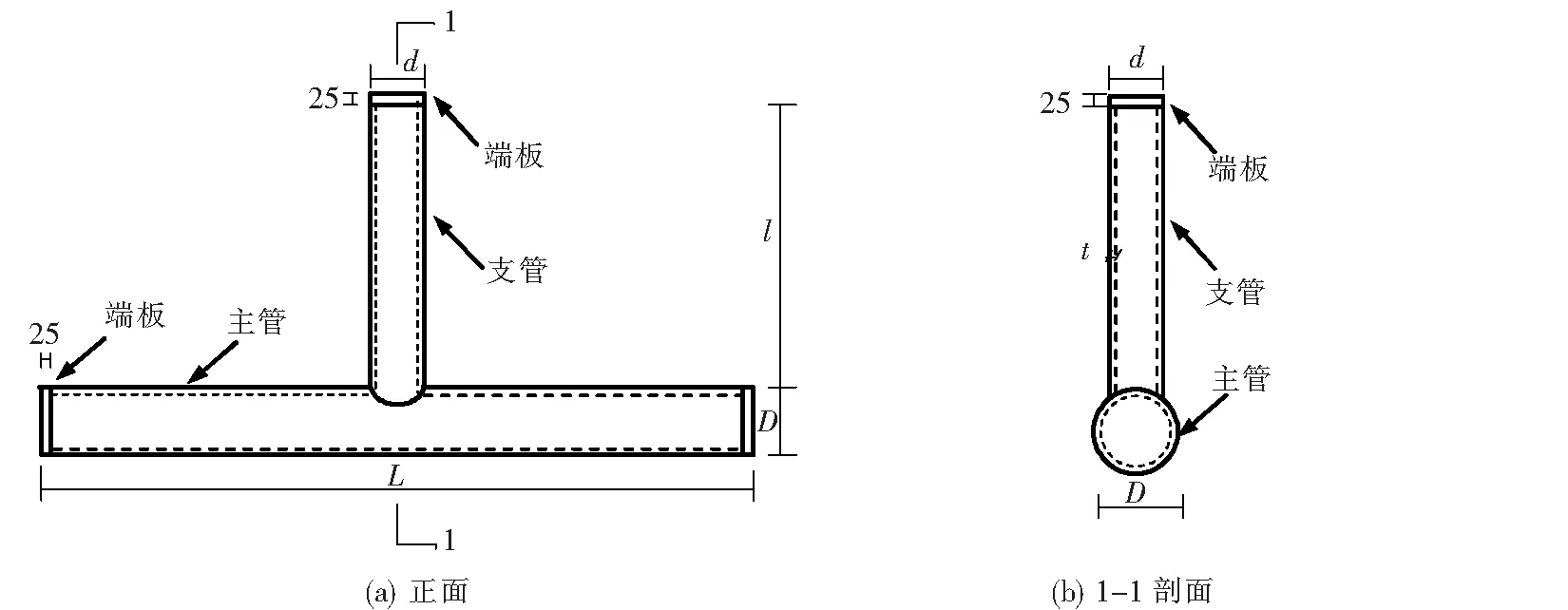
图1 T型管节点

表1 T型管节点模型参数及节点变形

1.2 材料特性

钢材是典型的率相关材料,遭受冲击荷载时,材料会产生率相关特性[14],随着应变率的提高,钢材屈服强度、强化阶段的平均应力和极限强度均有所提高．参考文献[12]中对T型管节点的试验设置,取模拟冲击速度为7.57 m/s,对此类低应变率钢材,应选用Cowper-Symonds模型,如式(1):

(1)

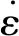
1.3 边界条件、界面处理、荷载施加、网格化分

图2给出了有限元冲击模型．主管右端U1、U2、U3、UR1、UR2、UR3被完全约束,用来模拟固定支座;主管左端可以发生轴向位移,需放开U3约束,模拟滑动支座．在主管左端设置弹簧,弹簧和主管端板连接采用耦合;弹簧左侧固定所有约束．所有端板与钢管端部采均采用绑定连接．

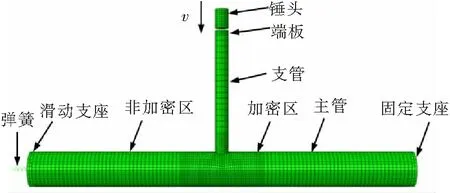
图2 荷载和边界条件

落锤与支管端板接触方式为通用接触,接触面包括切向和法向2个属性．法向关系为硬接触;切向关系运用库伦摩擦模型模拟接触面产生的滑动摩擦,库伦摩擦系数取值参考LS-DYNA原理手册[15],摩擦系数设置为0.42．

荷载的施加分为2个阶段．第一阶段,轴力施加阶段,通过改变弹簧的压缩量来施加主管轴力．第二阶段,动力分析阶段．将静力模型导入动力模型中进行显示分析,同时为导入模型的锤头赋予速度和重力,以此研究重力、轴力、冲击力三者共同作用下的抗冲击性能．

参考叶卉[12]中的T型管节点有限元模型,本文模型采用减缩积分三维八节点实体单元(C3D8R)．在遭受冲击荷载时,冲击破坏主要发生在T型管节点的节点相贯处,为了节省模型运算时间并保证节点区域应力应变精度,划分模型网格时应设置加密区与非加密区．网格化分越密,计算结果越精确,由于节点相贯处和锤头受力较大,节点区域变形较大,所以节点相贯区域应加密网格,网格单元尺寸为10 mm;主管其他区域变形较小,采用稀疏单元进行网格化分,网格单元尺寸为20 mm;支管受力时变形较小,网格化分密度较稀疏,网格单元尺寸为30 mm．

1.4 模型验证

图3—5给出了文献[12]中T型管节点T-1和T-2的试验结果和有限元计算结果．从图3(a)、(b)中可以看出,无论是节点相贯处的横截面,还是节点纵向断面的变形模态,有限元模拟结果与试验结果均吻合较好．节点变形主要集中在节点相贯处,且主管上表面上产生了较明显的局部凹陷和鼓曲．

图3 试验和有限元模拟变形结果比较

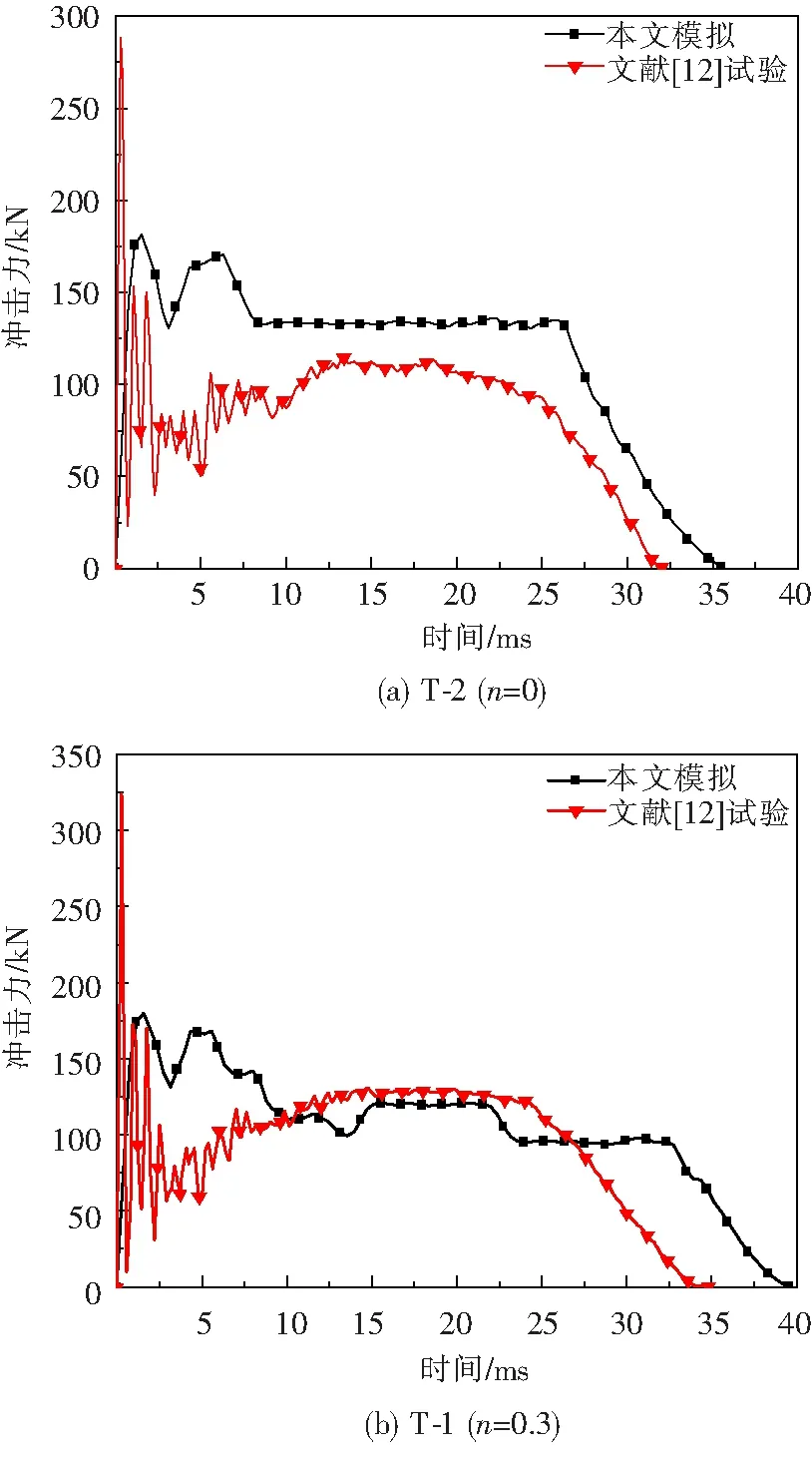
图4 文献[12]与有限元模拟冲击力时程曲线对比

and finite element simulation of impact force

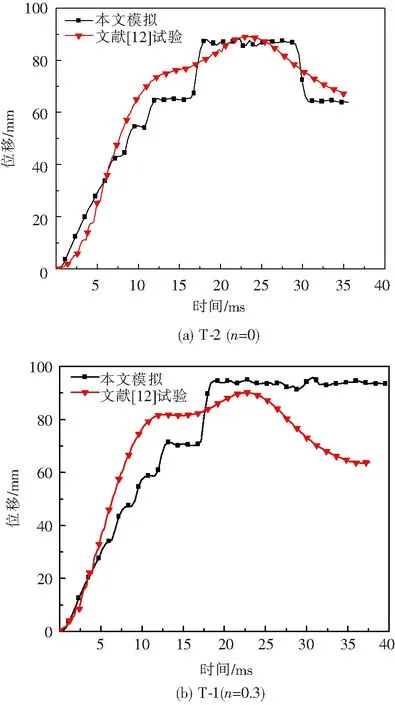
图5 文献[12]与有限元模拟位移时程曲线对比

ment simulated displacement time-history curve

图4和图5分别给出了试件T-1、T-2、J-1、J-2的节点冲击力和位移时程曲线．由冲击力时程曲线可知,试验得到的冲击力峰值比模拟得到的峰值大,有限元模拟得到的冲击力持续时间比试验得到的冲击力持续时间要长．经过对比冲击力和位移时程曲线,试验和模拟的曲线发展趋势是一致的,但模拟结果的冲击时间要比试验结果长,这是因为在试验中由于摩擦或者初始缺陷使得试验过程中试件抗冲击的时间缩短,所以试验时间偏短．有限元模拟和试验结果基本一致,数据基本吻合,为下一步的参数分析提供了依据．

2 有限元分析结果

2.1 破坏模态

T型管节点在最终时刻的整体变形和横剖面变形如图6所示．从4个T型管节点的破坏模态可以看出, T型管节点在冲击荷载作用下的变形包括主要分为2种,即节点相贯处的局部凹陷变形和整体弯曲变形．

从图6和表1可以看出,当轴压比为0和0.3时,T型管节点J-1、J-2整体变形较小,分别为20.67 mm和34.56 mm,试件的局部凹陷变形要大于整体变形,主管相贯处的横向鼓曲变形较小;当轴压比为大于0.6时,T型管节点J-3、J- 4的横向鼓曲变形、整体弯曲变形和局部凹陷变形迅速发展,且整体变形要大于局部变形,当轴压比为0.9时,试件的整体

图6 不同轴压比下T型管节点的破坏模态

弯曲变形和局部凹陷变形分别为127.97 mm和107.85 mm,同时主管横向鼓曲严重,呈现半圆形状．T型管节点的变形随着轴压比的增大而迅速增大,其原因是:冲击荷载导致主管发生整体弯曲变形和局部凹陷变形,在轴压力作用下产生二阶效应,轴压比较大时,二阶效应产生的附加弯矩越大,管节点的变形越大．

另外,随着轴压比的增大,在冲击过程中支管会产生明显的倾斜．原因是主管在轴力和冲击力的共同作用下,会产生严重的局部凹陷变形和整体弯曲变形,导致主管产生轴向收缩;由于主管右端固支,左端为滑动支座,故支管底部会产生向右的位移,导致支管发生倾斜．轴压比越大,主管向下弯曲变形越大,主管轴向收缩越大,支管倾斜幅度越大．说明了轴压比的增大会降低T型管节点抗冲击性能．

2.2 冲击力和变形分析

不同轴压比下的T型管节点的冲击力、整体位移、局部位移时程曲线如图7所示．整体变形为主管长度l/2处对应的主管底部位移量,局部凹陷变形为支管位移量减去整体变形位移量．根据锤头和支管的相对运动状态和时程曲线规律,冲击过程可分为以下4个阶段．第Ⅰ阶段:冲击力迅速增长阶段,落锤与支管接触碰撞,冲击力达到峰值,局部凹陷变形和整体变形开始发展,局部位移先于整体位移出现;第Ⅱ 阶段:震荡下降阶段,节点冲击力在震荡中逐渐下降;第Ⅲ 阶段:平台阶段,落锤和试件以近乎相同的速度向下运动,冲击力基本不变;第Ⅳ 阶段:平稳下降段,由于试件进入弹性恢复阶段,锤头向上运动,冲击力逐渐减小．

如图7所示,在冲击过程的第Ⅰ阶段,试件J-1、J-2、J-3冲击力峰值均出现在2.8 ms,峰值大小分别为181.5 kN、179.7 kN、175.7 kN,J-4的冲击力峰值出现在3.0 ms,峰值大小为159.2 kN．结果表明轴压比的增大会使T型管节点的冲击力峰值降低．从冲击力和变形出现的时间点可以看出,冲击力的增长早于变形发展,局部变形发展早于整体变形发展．原因是锤头和支管接触的瞬间,由于惯性作用,试件在冲击瞬间产生弹性激励并达到峰值冲击力,锤头冲击能量通过支管传递给主管,使其发生局部凹陷,局部凹陷无法吸收全部冲击能量,致使主管发生整体变形耗能．

冲击过程的第Ⅱ阶段,冲击力在震荡中下降,这是由于锤头的反弹、惯性效应和冲击波在锤头之间来回弹射造成的[16],同时局部凹陷和整体弯曲变形继续发展．

冲击过程的第Ⅲ阶段,试件J-1、J-2、J-3存在冲击力平台值,试件J-4没有平台值,整体弯曲变形值超过局部凹陷变形值,在此过程中,冲击力快速下降,节点发生整体失稳破坏．其原因是:试件节点处在冲击荷载作用下产生较大变形,截面面积减小,惯性矩减小,在较大轴压比下发生整体失稳破坏．

试件J-1、J-2、J-3存在第Ⅳ 阶段,冲击结束后有明显弹性恢复,试件J-4在冲击结束时,发生整体失稳破坏,此时的节点变形为塑性变形,无法产生弹性恢复．虽然图7(d)中虚线部分数据显示冲击过程仍在继续,但试件J-4已经发生整体失稳破坏,此时曲线不再有意义．

T型管节点的局部和整体变形如图7和表1所示．可看出,轴压比越大,节点变形越大,当轴压比大于0.6时,整体变形迅速增大,由n=0.6时的71.49 mm增大到n=0.9时的127.97 mm,局部变形由n=0.6时的58.88 mm迅速增大到n=0.9时的107.85 mm．故轴压比超过0.6时,T型管节点的整体弯曲变形和局部凹陷变形发展越快．由此可见,预加轴力越大,产生的二阶效应越显著,附加弯矩越大,致使局部凹陷和整体弯曲变形越大．可以得知,轴压比的增大会降低T型管节点的抗冲击性能．

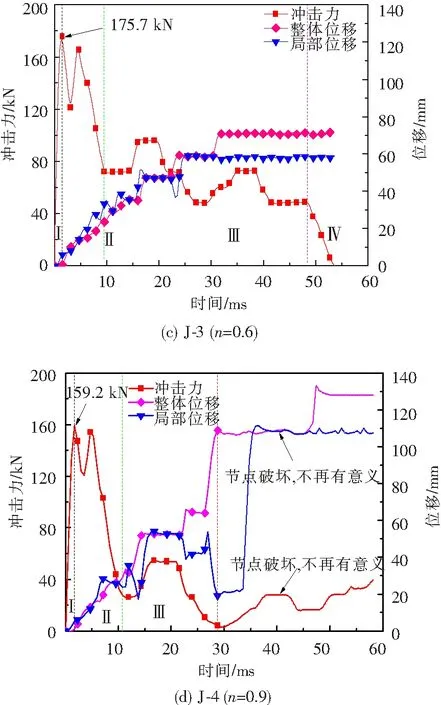
图7 冲击力和位移时程曲线

T型管节点的最大整体变形如图8所示,纵轴处代表主管L/2处的弯曲变形量,横轴代表主管长度．可以看出,随着轴压比的增大,T型管节点的最大整体变形逐渐增大．当轴压比小于0.6时,试件整体变形随轴压比的增大而小幅度增大;当轴压比为0.9时,试件变形迅速增长,主管在冲击荷载作用下发生整体失稳,形成塑性较,发生大幅度变形,管节点J-4不再具备承载能力．

图8 主管最大整体变形

3 不同轴压比下T型管节点抗冲击承载力分析

根据已有文献对抗冲击承载力的研究,本文结合动力荷载下的变形破坏准则[9-10]和冲击力时程曲线平台值[11],通过4种方法评估钢管节点的抗冲击承载力．

方法一, 节点的破坏准则可分为极限荷载准则和极限变形准则2种,极限荷载准则为取承载力为荷载的最大值,极限变形准则取变形δ达到某一限值(δmax=3%D)所对应的承载力,节点的极限承载力取极限强度准则和极限变形准则二者中的较小值,国际公认的准则为极限变形准则[17];冲击力和局部位移的关系如图9(a)所示,通过限定3%D的局部变形上限来评估钢管节点受到来自支管的轴向冲击荷载时的极限荷载承载力[9]．方法二,冲击力和整体位移的关系如图9(b)所示,以钢结构柱弹塑性层间位移角限值[10]中对应的(L/2)/50的整体变形上限来评估钢管节点受到来自支管的轴向冲击荷载时的整体变形极限承载力．方法三,使用《钢结构设计标准》(GB50017—2017)[13]所提供的公式计算

图9 冲击力与相关位移时程曲线

placement

静力荷载作用下T型管节点的节点承载力,且静力承载力要小于动力承载力[6],国内外学者通过建立动态屈服强度以及极限强度动力增大系数(DIF)表达式来考虑钢材的应变率效应．方法四,借鉴文献[11,18]中极限承载力的计算方法,以冲击力时程曲线平台值作为极限抗冲击承载力．

《钢结构设计标准》(GB50017—2017)[13]给出了静力荷载作用下T型管节点的承载力,如公式(2)所示:

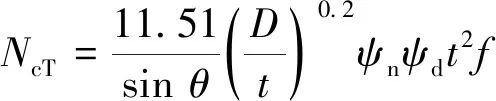
(2)

其中:NcT为节点承载力,θ为支管、主管夹角,D、t分别为主管直径和壁厚,ψn为与轴力有关的参数,ψd为与支管、主管直径有关的参数,f为主管钢材抗拉、抗压强度设计值．

表2给出了4种计算方法所得出的T型管节点极限承载力．分析表2可知,方法一以3%D的局部变形作为抗冲击极限承载力判断标准,其结果偏大,原因是极限变形准则用来计算节点的静力承载力,但节点在遭受动力荷载后,变形迅速增长,冲击力在冲击瞬间达到最大值,所得动力节点承载力较静力承载力偏大;方法二考虑了较大轴力产生的二阶效应对结构的影响,为防止管节点发生整体失稳破坏,根据《建筑抗震设计规范》(GB5011—2010)[10],以整体变形上限(L/2)/50作为T型管节点的抗冲击极限承载力;方法三用来计算静力荷载作用下的节点承载力,但动力冲击试验由于钢材的率相关效应,管节点在动力作用下的抗冲击承载力要大于静力承载力;方法四使用YOUSUF等[11]所提出的方法,即以图7中冲击力时程曲线的平台值作为节点的抗冲击承载力,但当轴压比达到0.9时,T型管节点不会出现平台值,结合图7和图8节点变形情况,T型管节点处形成塑性铰,变形急剧增大,无法评价T型管节点抗冲击承载力．

通过对比以上4种评价方法得出结论,以整体变形上限(L/2)/50作为评估T型管节点的抗冲击极限承载力是较为合适的评估方法．

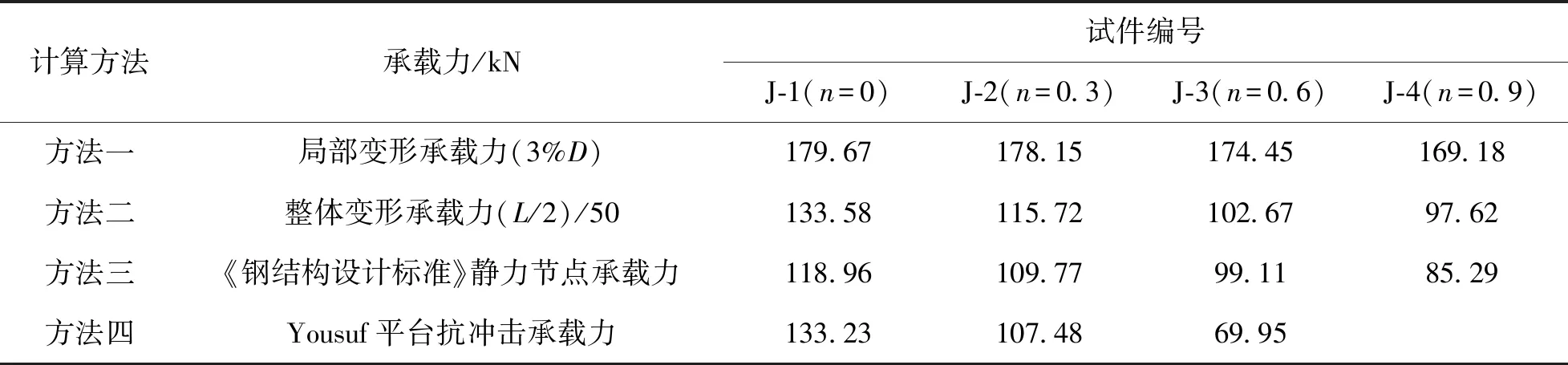
表2 不同轴压比下试件抗冲击承载力

4 结 论

本文通过对不同轴压比下的T型管节点的抗冲击性能进行有限元模拟,对T型管节点的破坏模态、冲击力和位移时程曲线、抗冲击承载力进行分析,得出以下结论:

(1)当轴压比为0、0.3、0.6时,T型管节点遭受冲击荷载后,破坏模态主要为支、主管相贯处的鼓曲破坏为主,当轴压比为0.9时,T型管节点的破坏模态主要为主管因产生塑性铰而发生整体失稳破坏;

(2)轴压比小于或等于0.3时,不同轴压比对T型管节点的局部凹陷变形和整体变形影响较小,当轴压比超过0.6时,节点的局部凹陷变形和整体变形迅速发展,轴压比的增大降低了T型管节点的抗冲击性能;

(3)对于承受轴压力的T型管节点,轴压比的增大会降低T型管节点的抗冲击承载力,对比4种抗冲击承载力计算方法,建议把节点整体变形上限(L/2)/50所对应的冲击力作为T型管节点的抗冲击极限承载力．