基于动力学缩减的长跨距管路系统振动特性分析

于 涛,曲虹全,王 潇,阎 旭,林佳玮,王彦琨

(1.烟台大学机电汽车工程学院,山东 烟台 264005; 2. 烟台工程职业技术学校电气与新能源工程系,山东 烟台 264006; 3. 烟台市知识产权保护中心,山东 烟台 264005)

在钻井平台中,管路系统担负着液压动力的输送任务,对机组的运转有着举足轻重的保障作用．管路系统具有复杂空间分布、长跨距和多点弹性支撑等特点,在基础激励、流体激励下易发生管路系统多点共振、大幅度振动等问题,特别是存在共振的情况下,管路系统产生大幅度振动导致支撑刚度的下降或连接接头的脱离,而高振动应力甚至会导致管路系统产生裂纹甚至断裂．因此对复杂管路系统进行动力学精确建模,获得其动力学特性至关重要．

国内外学者针对大型结构精确建模及相关试验进行大量的研究,如ERATH等[1]建立了复杂管路的动力学模型,采用有限元方法对管路进行了各点振动响应的分析,并进行试验验证．KRUISBRINK等[2]在复杂构型管路试验平台上测量了支撑变化情况下管路的固有频率,并总结出其中的变化规律．ZHAI等[3]研究了在受到随机激励时管路所具有的动态特性．LEE等[4]利用有限元的方法建立了管路模型,分析了刚度和阻尼在有限元模型中的变化情况．OUYANG等[5]采用一维管道模型分析了复杂液压管路的频率特性,并通过试验与数值模拟验证了一维管道模型计算的准确性．RAHEBCA[6]采用梁模型建立直管和弯管的传递矩阵,对多弯管结构进行了计算,通过分析确认了在低频情况下梁模型理论解析的正确性．TIJSSELING等[7]建立的输流管路系统动力学方程包含多个变量,应用特征线方法求解了方程．曾骥等[8]采用有限元分析软件CAESARII对高压泥浆管路进行了应力仿真分析,并基于电测法进行了管路危险部位应力的对比测试,其试验数据与有限元仿真结果误差在15%以内．于长波等[9]采用有限元方法,对多层U型波纹管的强度进行了计算分析,给出了较为准确的结果．王建功等[10]采用有限元和工程方法计算管路补偿位移疲劳寿命和耐久振动寿命,经过试验对比,有限元分析方法精度高于工程方法．

对于模型缩减的基础,是20世纪60年代初HURTY[11]首先提出固定界面模态综合法,随后,CRAIG和BAMPTON[12]于1968年对HURTY的理论做了部分修正,现代所常用的固定界面模态综合法就是CRAIG和BAMPTON提出的优化理论．基于模态综合法和有限元模型修正相结合的方法对大型结构进行综合缩减,获得了较高的计算精度[13]．模态综合法在不确定性分析[14]、结构优化[15]、纳米结构[16]、机械结构系统[17-18]等领域得到了应用．

针对管路系统,缺乏关于管路振动高效率建模分析方法的研究,本文采用模型缩减方法对空间受限和长跨距管路结构进行合理的简化,用简单的有限元模型代替复杂的管路结构,并保留管路系统主要的动力学特征．首先将管路系统按支撑边界分割为若干管路段,选定主要研究管路段和模型缩减管路段,进行子系统的模型缩减;最后通过试验和有限元计算对照,验证本文提出的管路模型缩减方法的有效性．

1 管路系统动力学建模

1.1 复杂管路系统动力学分析

选取液压系统中一段由液压泵到执行元件管路为研究对象,即管路系统一端连接液压泵,另一端为执行机构,管路系统的结构示意如图1所示,管路内径为r1,外径为r2,材料密度为ρ,弹性模量为E,泊松比为μ．由于管路系统比较庞大、复杂、组件多,所以在振动特性研究中对管路系统进行简化,即管路左侧可以简化成固支约束,分别在A、B、C段的右处简化为卡箍支撑,分析的管路系统如图1．

图1 管路系统结构

1.2 基于有限元法的管路系统建模

为了提高网格质量,减少运算时间,将与模态计算关系不大的模型中的倒角、小孔等特征删除,分析中采用高阶三维实体单元Solid186实体单元进行有限元模型的网格划分,共划分了4000个单元,整体管路建模如图2．

图2 管路系统的有限元建模

模态计算约束条件为一端固定约束,3个卡箍支撑,固定约束为约束一个端面上所有节点;由于管路安装空间有限,管路卡箍是固定管路并抑制振动的一种常用元件,选取弹支刚度为Ku=Kv=Kw=2×105N/m,根据卡箍的结构和功能特点,卡箍约束简化成3个沿x、y和z轴Combine14弹簧单元,并将弹簧单元中心节点耦合到管路体上,边界条件施加如图3,选取管路的几何参数如表1．

图3 管路边界条件施加

表1 管路的材料属性和几何参数

1.3 管路系统振动特性分析

分析频率范围为0～1000 Hz,从有限元计算所得振型看,每一个频率对应2个振型(2个方向的振型),选择y方向作为分析振型,选取的分析振型如图4．

图4 管路振型频率范围(0～1000 Hz)

由振型图可知,振型对应频率与分割管路段自身频率相近时,分割管路振型为自身的一阶弯曲,并且以自身的振动引起临近管路段的振型,从而导致管路段的耦合振动．

分析频率区为1000～3000 Hz,选取的分析振型如图5．

图5 管路振型频率范围(1000～3000 Hz)

由管路的振型图可知,频率区1000～3000 Hz对应的振型是弯曲振动,为分割管路的二三阶弯曲振型,并且以自身的振动引起临近管路段的二三阶弯曲振动,振型中存在管路段耦合振动．

2 复杂管路系统模型缩减方法

2.1 模型缩减理论基础

针对液压管路在特定区段振动特性分析的需求,采用模态综合法的思想进行模型缩减．

以卡箍为边界将管路分割,在对应的边界条件下进行各个管路段的模态分析,即A段管路为一端弹支,一端固支约束,B段管路为两端弹支,C段管路为两端弹支,各管路段有限元模型见图6．

图6 管路段有限元模型

将管路划分为n个子系统,对于各个管路子系统,其一般动力学方程表达为

(1)

其中:i=1,2,…,n表示为子系统的名称,qI为内部节点坐标,qJ为界面节点坐标,fJ(t)为界面力,I为内部节点,J为界面节点．

子系统在模态坐标p下的运动方程为

(2)

其中,ΦII为子系统主模态,Ψc为界面约束模态矩阵,其表达式为

(3)

选取子系统前m阶振型参与模态综合,得到降阶后子系统的质量、刚度和阻尼矩阵为

(4)

对式(4)降阶后的子系统1,2,…,n进行整体组集,得到整体质量矩阵为M、K和C消去边界耦合处模态坐标不独立模态坐标,得到为变换矩阵Ψ,因此,管路系统模型缩减后的动力学方程为

(5)

式(5)中,M*=ΦTMΦ,K*=ΦTKΦ,C*=ΦTCΦ,

2.2 模型缩减法系统建模

以弹性支撑处为边界将整体管路分割成A、B、C三段,B段管路为关注区段,利用模型缩减原理获得A、C段管路对B段管路的作用,即将A、C段管路计算为超单元,B段管路的边界条件不变,进而展开空间受限管路的振动分析．根据模型,划分关注区段如图7．

图7 关注区段划分

根据划分原则,将管路系统划分为若干子系统,根据管路在宽频范围内振动特性分析的需求,选择合适的缩减模态阶次,将各个子系统进行模型缩减,然后将缩减模型进行整体组集,得到管路系统的缩减模型,缩减原理图如图8．

图8 管路系统模型缩减原理

将区段A、C缩减为超单元,超单元类型选择Matrix50,Matrix50单元是一组预先装配好的单元,任何ansys中的模型都可以生成的超级单元．关注区段B段管路仍旧保留原有的边界条件,定义接触面和单元集合,求解缩减区段A、C的固有频率．

图9 超单元

2.3 特定管路段的固有特性分析

从固有频率、振型和谐响应分析几个方面进行比较,模型缩减后的固有频率对比分析如表2,关注区段B的振型如图10．

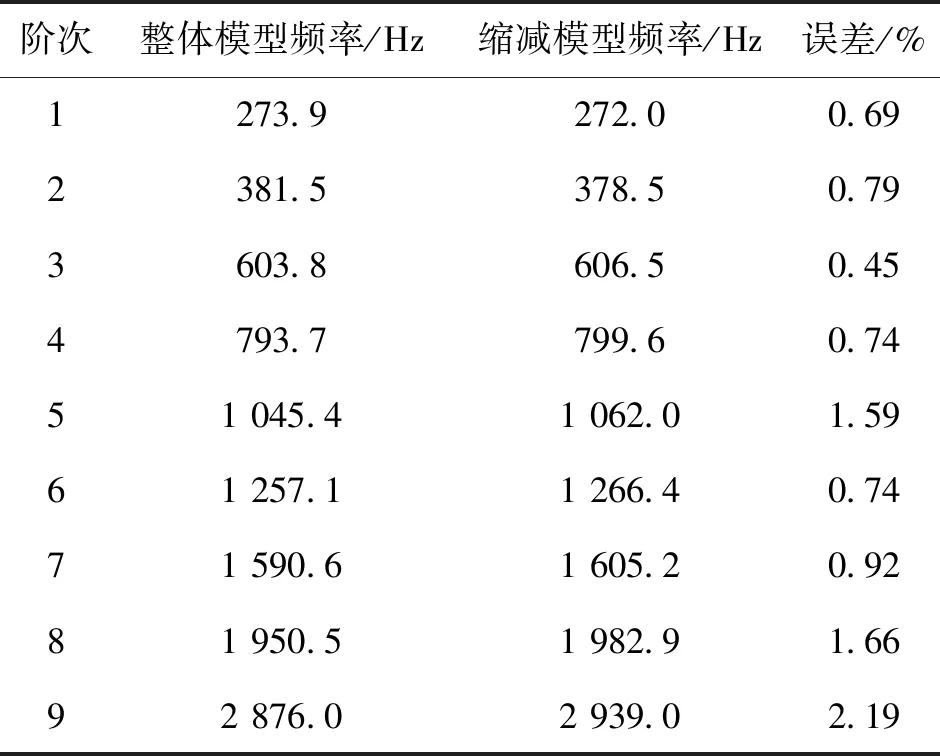
表2 缩减后的固有频率对比

图10 缩减模型振型

频率范围为0～3000 Hz,选择y方向位移的最大的振型作为分析振型,选取的分析振型如图10．

根据表2,从固有特性的角度分析,整体模型和缩减模型的管路固有频率基本一致,最大误差为2.19%,误差在允许范围内;根据图10对比管路系统的振型可以看出管路系统振型与缩减模型的振型具有一致性,缩减模型可以准确反映特定管路的振型特性．因此,缩减模型可以代替管路系统进行管路的振动特性研究．

2.4 基于模型缩减的基础激励下管路系统的响应预估

对管路进行基础激励下的谐响应分析,即计算管路在承受简谐载荷时的稳态响应．利用半功率带宽法识别管路系统的模态损耗因子,考虑将管路系统的结构阻尼考虑为瑞利阻尼,得到瑞利阻尼系数分别为:α=14.903,β=2.4×10-6．提取在基础激励条件下的振动幅值与频率曲线,并以一阶固有频率对应的幅频曲线与整体管路在相同条件下的幅频曲线做对比,所得曲线如图11．

图11 模型缩减前后谐响应分析对比

从图11中可以看出,通过结构在不同频率在和作用下的响应值比较,管路模型和缩减模型的固有频率没有缺失且误差较小．因此,建立较为精准的缩减模型可以为复杂管路的建模提供便捷及可靠的研究方法．

2.5 计算效率比较

为了定量比较管路模型和缩减模型计算效率的差异,对比了2种模型在同一台计算机上(CPU: AMD R5 2600,频率:3.4 GHz,内存:16 GB,固态:1 TB)完成运算所需要的时间．

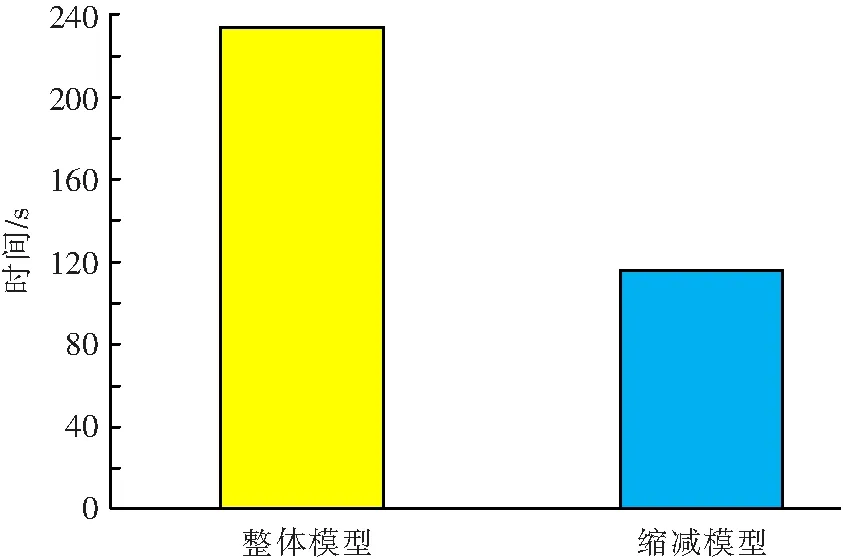
图12 计算时间比较

如图12,整体模型的运算时间为234 s,缩减模型的运算时间为116 s．计算结果显示,模型缩减方法可以将计算效率提高一倍左右．在工程应用中,使用模型缩减方法有着更高的计算效率,可以减少计算时间．

3 试验研究

搭建了管路振动测试试验台．该实验台的结构组成主要包括:底座、试验件(包括管路、卡箍等),LMS数据采集系统、传感器和激励装置,测试实验台搭建见图13．

图13 振动测试环境

在试验研究时,采用锤击法在管路上选取的多个锤击点进行敲击,利用LMS数据采集系统,获得管路系统的振动响应信号,以获得管路的固有频率,锤击法所得频率如表3,试验所得管路系统的响应信号如图14．

通过表3中数据对比可知,锤击法试验所得管路频率值除3、6、9阶固有频率外,其他固有频率基本一致,得到的频率值与缩减模型计算得到频率误差在6.25%以内,说明管路系统的计算结果与试验测试吻合良好,从而进一步验证了本文所提出的采用模态综合法缩减模型的有效性．

表3 管路固有频率数值计算与试验测试结果对比

图14 管路系统的振动响应

4 结 论

本文提出一种基于模型缩减的管路系统振动分析方法,以某典型管路系统为例,从固有频率、振型、振动响应以及计算效率几个角度分析获得结论如下:

(1)管路系统是一个整体系统,各个区段耦合振动现象明显,管路系统缩减模型与整体模型在宽频域内固有频率和振型保持一致,从而验证了缩减模型与原模型具有相同的模态特性．

(2)将缩减模型与整体模型计算效率进行对比．缩减模型的计算时间远小于整体模型,可以显著提高计算效率,减少计算时间．

(3)搭建了管路系统平台测试响应特性．测试结果表明,管路系统缩减模型的固有特性和响应特性可以较好地吻合,证明了缩减模型方法的精度及可行性,验证采用模态综合法缩减模型可以为管路系统振动特性分析提供一种新的方法．