中立型随机非线性系统解的噪声到状态渐近有界性

任 丽,吕 文

(烟台大学数学与信息科学学院，山东 烟台 264005)

随机微分方程被广泛应用于经济、生物、物理、自动化、金融等领域，在系统分析过程中，稳定性和有界性理论是研究的2个重要方面，近几十年来，对随机微分方程的研究吸引了人们广泛的关注，例如文献[1-5].

中立型随机微分方程不同于一般的方程之处在于它的导数项里也带有时滞，依赖于过去和现在的值，HALE 和LUNEL[6]对这类方程的研究做出了很大的贡献.在考虑环境扰动的情况下，KOLMANOVSKII和NOSOV[7]、MAO[8]讨论了由Brownian驱动的时滞中立型随机微分方程.2018 年，LV[9]提出了具有如下形式的中立型随机非线性系统(1)，分析了在全局Lipschitz、 局部Lipschitz和线性增长条件下的解的存在唯一性，给出系统的噪声到状态p阶矩指数稳定性；本文在LU[9]基础上，用其他的条件替换掉线性增长条件得到了系统(1)解的存在唯一性定理，进而给出系统解的p阶矩噪声到状态渐近有界性和p阶矩噪声到状态稳定性,

F(x(t),x(t-τ),t)dt+

G(x(t),x(t-τ),t)ξ(t)dt，t≥t0,

(1)

其中，方程中的初值是xt0,ξ(t)是二阶矩过程.

DENG等[10]、KRSTIC等[11]对Brownian随机非线性系统提出了噪声到状态稳定的概念；随后，ZHANG等[12]研究了具有二阶平稳过程的状态切换随机非线性系统的噪声到状态稳定性，继而ZHANG等[13]在二阶过程合理假设下建立了随机切换系统的噪声到状态稳定性准则.后来，人们对此类问题进行了大量的研究，例如，XIE 和ZHANG[14]研究了中立型随机微分方程的稳定性和渐近有界性.

本文第1节中将介绍所用到的基本概念，第2节中，讨论中立型随机非线性系统的解的存在唯一性；第3节中将考虑系统解的p阶矩噪声到状态渐近有界性，最后给出一个关于p阶矩噪声到状态稳定性的推论.

1 预备知识和基本假设

首先给出本文将用到的基本符号和引理.

(Ω,F,Ft,P)是给定的完备可测空间，其中流{Ft}t≥0满足通常条件；对任意的p>0, 记

本文将考虑如下中立型随机非线性系统:

G(x(t),x(t-τ),t)ξ(t)dt，t≥t0,

(2)

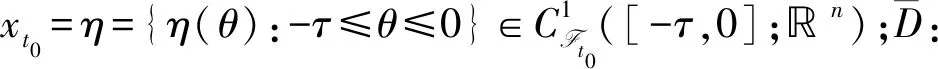
(A1)ξ(t)∈d是 Ft-适应的，满足分段连续，且存在参数c0,d0，使得

(A3)存在κ∈(0，1)使得对任意的x∈n，有

定义1 对任意的t≥t0-τ，称x(t):=x(t,t0,x(t0-τ))是系统(2) 的一个解，如果x(t)满足：

(1) 对任意的t≥t0-τ，x(t)是连续并且 Ft-适应的，当t∈[t0-τ,t0], 满足Ft≡Ft0;

(3)对任意的T>t0,下列等式成立:

定义2 若存在常数δ≥0和一类Κ类函数γ(·)使得

称非线性系统(2)的解是p阶矩噪声到状态渐近有界的.

定义3 设p>0，若存在正常数c、λ和Κ类函数γ(·)，使得对任意t≥t0有

称随机非线性系统(2)是p阶矩噪声到状态指数稳定的.

以下引理参见文献[9].

引理1 设p≥1，假设(A3)成立，则对任意的x,y∈n，有

α1-λc2}(1+κ)p-1-

eλτ(α2+κλc2(1+κ)p-1)=0，

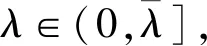
其中:

τeλτ(α2+κλc2(1+κ)p-1].

引理3 假设(A1)、(A2)成立，则中立型随机非线性系统(2) 在区间[t0,σ∞)上存在唯一解.

2 解的存在唯一性

在本节中，将给出系统(2)解的存在唯一性定理，首先给出如下假设:

(A4)假设存在正常数c1,c2，α1,α2,α3,d,α1>α2,C1函数V(x,t):n×[t0,∞)→+使得对p≥1，∀t≥t0,x,y∈n,

c1|x|p≤V(x,t)≤c2|x|p;

(3)

-α1|x|p+α2|y|p+α3.

(4)

定理1 假设(A1)—(A4)成立，则中立型随机非线性系统(2)存在唯一解.

-α1|x(t)|p+α2|x(t-τ)|p+

对不等式两边积分并求期望，由假设(A3)和式(3)得

c2(1+κ)p-1E(|x(t0)|p+κ|x(t0-τ)|p)+

c2(1+κ)p-1E(‖η‖p+κ‖η‖p)+

由于

类似于文献[15]中引理5的证明过程，易得σ∞=∞.a.s. 即方程(2) 存在全局唯一解. 证毕.

3 p阶矩噪声到状态渐近有界性

本节中，我们考虑中立型随机非线性系统(2) 解的p阶矩噪声到状态渐近有界性.

eλtE|x(t)|p≤κeλtE|x(t-τ)|p+

由于

代入上式得

化简得

从而

两边同乘e-λt得

E|x(t)|p≤

令t→∞，得

即中立型随机非线性系统(2) 的解是p阶矩噪声到状态渐近有界的. 证毕.

对上述定理2，令α3=0，可得文献[9]中的定理3.

推论设定理2的假设成立且α3=0，则中立型随机非线性系统(2) 是p阶矩噪声到状态指数稳定的.

证明由定理2的证明，令α3=0，得

E|x(t)|p≤

即中立型随机非线性系统(2)是p阶矩噪声到状态指数稳定的. 证毕.