2020年高考全国Ⅲ卷第23题的证法探究

重庆三峡学院数学与统计学院 (404000) 程凤娟 胡 艳

数学探究越来越受到人们的关注.如何作数学探究是数学教学必须面对的问题.历年的高考试题具有典型性和导向性，探究其解法及其背景和考试功能对教学是十分有益的，本文拟就2020年高考全国Ⅲ卷中不等式选讲部分的考题的证明方法作一探究.

1.原题呈现

对于第(1)问，利用恒等式(a+b+c)2=a2+b2+c2+2ab+2bc+2ca及已知条件即得；而对于问题(2)，由于题干中出现了max{a,b,c}，使得该考题一改过去不等式考题中常见的绝对值或代数不等式的形式，增加了试题的难度.对于这种题型，如何证明呢？

2.证法探究

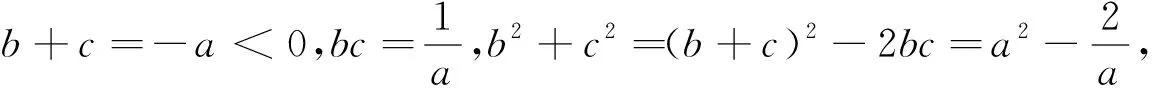
分析2:利用二元柯西不等式(b+c)2≤(12+12)(b2+c2).

分析3:利用恒等式(b+c)2-4bc=(b-c)2.

分析4:利用条件恒等式a+b+c=0时a3+b3+c3=3abc.

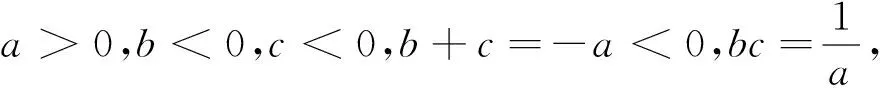
分析5:由b+c及bc，将b,c看作是一元二次方程的二根，利用韦达定理的逆构造方程.

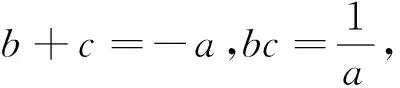
分析6:由a+b+c=0及abc=1，利用平面解析几何中直线与曲线相交的条件.

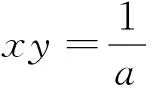
分析7:反证法是不等式证明中的一种重要方法，十分有用，而对于本题则有：

转化是数学解题的基本途径，而建立知识之间的联系给解题提供了广阔的思维空间，通过长期不懈的努力，必能抓住数学的本质特征、领悟数学学科的核心价值，同时还能加深对数学思想方法的理解与掌握，这对数学核心素养的养成是十分有用的.