例析多元函数累次最值法的应用

江西省吉安市白鹭洲中学 (343000) 吴望茂

多元函数最值问题是中学数学竞赛的热点和难点，而多元函数最值问题的一般解决方法需用到高等数学，此已超出中学数学范围.限于中学数学范围，此类问题的解决难度大，技巧性高，无固定模式可循.为此，我们提出一种具有普遍意义和实用价值的初等方法，我们称之为“累次最值法”.

二元函数累次最值法：对于平面区域Ω上的实二元函数f(x，y)，设Ω中所有点(x，y)的横坐标x的集合为X={x|(x,y)∈Ω}；对任意固定的x∈X，记Ω中所有横坐标为x的点(x，y)的纵坐标y之集合为Yx={y|(x,y)∈Ω}.

实际上，二元函数累次最值法的思想是降维转化与逐步逼近.所谓降维转化，就是把二元函数最值问题转化为两次单元函数最值问题；所谓逐步逼近，就是于最大值之中寻找最大者，于最小值之中寻找最小者.对于平面区域Ω上二元函数f(x，y)的最值问题，其解题步骤是：

(1)对任意固定的x∈X={x|(x,y)∈Ω}，视f(x，y)为y的函数，求f(x，y)在Yx={y|(x,y)∈Ω}上的最值，结果是x的函数φ(x);

(2)令x在X中变化，求φ(x)在X上的最值，此即f(x,y)在Ω上的最值.

与二元函数类比，我们可以将上述方法推广到n元函数，建立以下n元函数累次最值法：

相应地，n元函数累次最值法的思想也是降维转化与逐步逼近.对于n元函数f(x1,x2,…,xn)的最值问题，首先对任意固定的x1,x2,…,xn-1，视f(x1,x2,…,xn)为xn的函数，求其最值，结果是x1,x2,…,xn-1的函数φ(x1,x2,…,xn-1)；再把此n-1元函数φ(x1,x2,…,xn-1)的最值问题降维转化为n-2元函数最值问题；如此继续降维转化，直到转化为n次单元函数最值问题.

例1 (2013年新加坡数学奥林匹克试题)设x,y,z均为正实数，求W=

(1)对任意固定的x>0,y>0,视f(x,y,z)(z>0)为z的函数，f(x,y,z)=

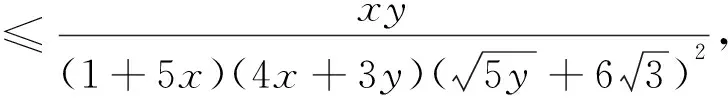
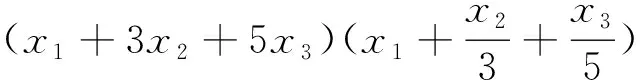
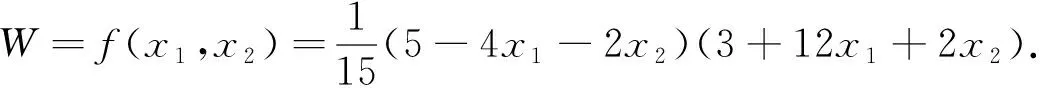
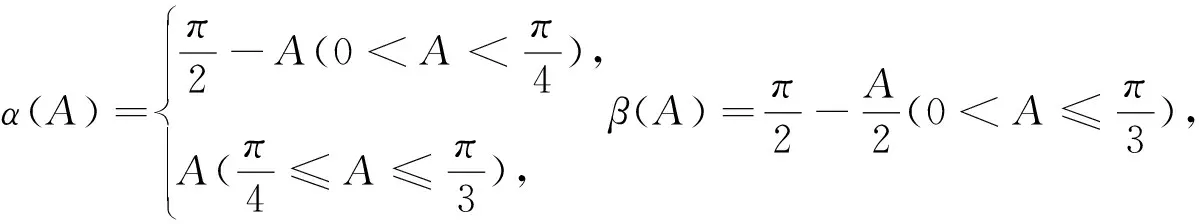
多元函数累次最值法，虽然其解题过程略显繁复，但其思路清晰自然，解题方法程序化，具有普遍意义和实用价值.