函数图像切线问题“大盘点”
江苏省溧水高级中学 (211200) 方金宝
导数的几何意义就是曲线在该点处切线的斜率.用导数的几何意义研究曲线切线的有关问题是导数最基本的应用,也是近年高考的一个热点.本文以2019年的高考试题为例进行剖析,力求揭示此类试题的考查形式,探索它们的求解策略.
题型一:求切线方程
例1 (2019年全国Ⅰ卷理科13题)曲线y=3(x2+x)ex在点(0,0)处的切线方程为.
解:∵y′=3(2x+1)ex+3(x2+x)ex=3(x2+3x+1)ex,∴曲线在点(0,0)处切线的斜率k=3,∴切线方程为y=3x.
例2 (2019年江苏卷11题)在平面直角坐标系xOy中,点A在曲线y=lnx上,且该曲线在点A处的切线l经过点(-e,-1)(e为自然对数的底数),则点A的坐标是.
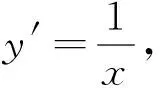
考查函数H(x)=xlnx,当x∈(0,1)时,H(x)<0;当x∈(1,+∞)时,H(x)>0,且H′(x)=lnx+1,当x>1时,有H′(x)>0,从而H(x)单调递增,注意到H(e)=e,故x0lnx0=e存在唯一的实数根x0=e,故A(e,1).
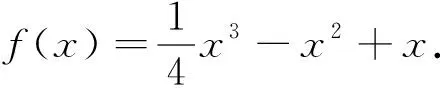
(Ⅰ)求曲线y=f(x)的斜率为1的切线方程;
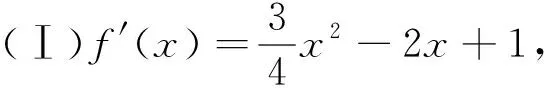
点评:曲线切线方程的求法可分为已知切点(如在点处的切线)和未知切点(如过点的切线和已知斜率的切线)两种类型:(1)已知切点(x0,f(x0))求切线方程的步骤:①求出函数f(x)的导数f′(x);②求切线的斜率f′(x0);③写出切线方程y-f(x0)=f′(x0)(x-x0),并化简.(2)未知切点求切线方程的步骤:①设出切点(x0,f(x0));②求出函数f(x)的导数f′(x);③求切线的斜率f′(x0);④写出切线方程y-f(x0)=f′(x0)(x-x0);⑤代入其它条件解出切点坐标;⑥把切点(x0,f(x0))重新代入切线方程并化简.
题型二 求参数的值
例4 (2019年全国Ⅲ卷理科6题)已知曲线y=aex+xlnx在点(1,ae)处的切线方程为y=2x+b,则( ).
A.a=e,b=-1B.a=e,b=1
C.a=e-1,b=1D.a=e-1,b=-1.
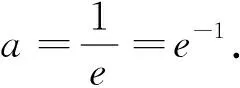
点评:利用切线方程求参数的值是切线问题的逆向应用,例4通过求导数得到切线斜率的表达式,根据斜率为2解得a,再将切点坐标代入直线方程求得b.在这一过程中主要运用了方程思想和待定系数法.
题型三 求距离最值
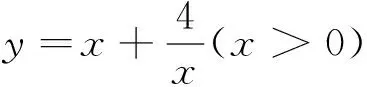

点评:很多曲线上的动点到直线距离的最值问题都可以用数形结合思想,把它转化为切线切点到直线的距离,当然本题也可以使用公式法结合基本不等式来处理.
题型四 公切线证明

(1)讨论函数f(x)的单调性,并证明函数f(x)有且只有两个零点;
(2)设x0是f(x)的一个零点,证明曲线y=lnx在点A(x0,lnx0)处的切线也是曲线y=ex的切线.
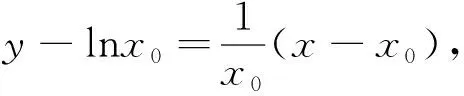
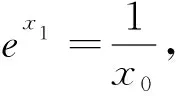
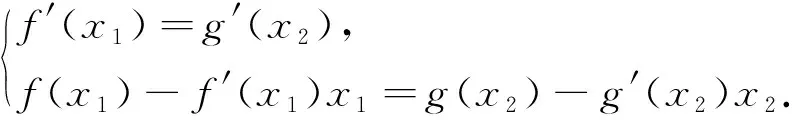
通过2019年高考试题的研究分析我们发现,函数图像的切线问题根据切线已知条件的不同,主要有“曲线在某点的切线”、“曲线过某点的切线”、“已知斜率的切线”以及“两曲线的公切线”等四种常见类型;根据题型的不同,主要有“求切线方程”、“求参数的值”、“求距离最值”以及“公切线证明”等四种常见题型.其实无论哪种问题,我们只需抓住该问题的核心和处理该问题的一些常见数学思想如方程思想、数形结合思想、分类讨论思想、转化和化归思想等.切线问题的核心其实就是切点,一个函数的切线要关注已知点是否为切点,两个函数的切线要关注切点是否同一,牢牢抓住切点,问题便迎刃而解.

