用向量法推证的三角形一个有趣定理
2020-11-04 06:51广州大学附属中学510006朱惊涛
中学数学研究(江西) 2020年10期
广州大学附属中学 (510006) 朱惊涛

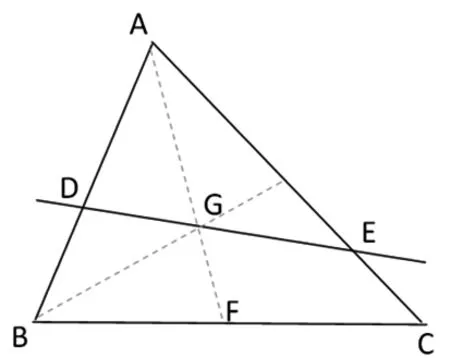
图1

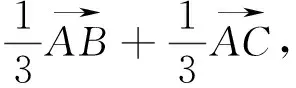

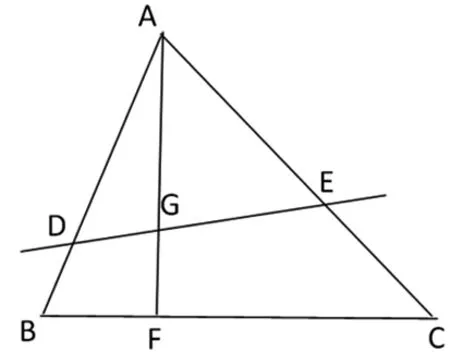
图2
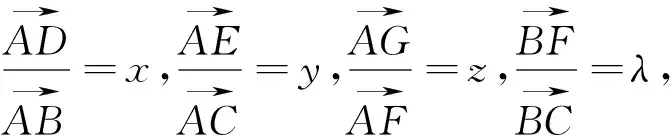

该结论的简单形式如下:

在该定理中,分别令x=1、y=1、z=1可以得到它的三种特殊化情形,如图3、图4、图5所示:

图3 图4 图5
该定理有助于解决一些三角形内的线段比例问题,并可以推出一些有趣结论或证明一些经典的定理,试看以下一些例子.

图6
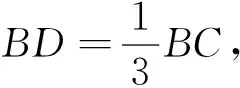



图7

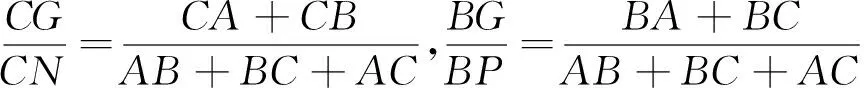

图8

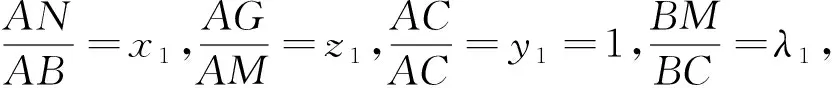
该结论说明形如图9的图形模块,必有性质:

图9

例4 (证明梅涅劳斯定理)如图10,如果一条直线与ΔABC的三边AB、BC、CA或其延长线交于F、D、E点,那么

图10


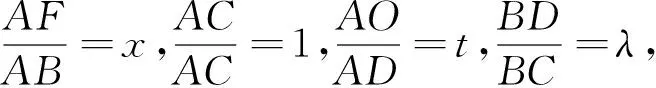


通过例4、例5、例6可知该定理的特殊情况实质上是与梅氏定理、塞瓦定理、三角形比例线段和定理相通的.利用该定理还可以解决一些立几和解几中的相关问题,试再看以下两例:

图11
例7 如图11,证明正四面体的内切球与外接球的半径之比是1∶3.
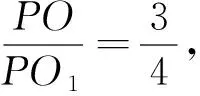

图12
例8 (2019年高考浙江卷)如图12,已知点F(1,0)为抛物线y2=2px(p>0)的焦点,过点F的直线交抛物线于A、B两点,点C在抛物线上,使得ΔABC的重心G在x轴上,直线AC交x轴于点Q,且Q在点F的右侧.记ΔAFG,ΔCQG的面积分别为S1,S2.
(1)求p的值及抛物线的准线方程;
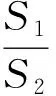
析解:(1)易得抛物线方程为y2=4x,p=2,准线方程为x=-1.
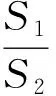

图13


类似于梅氏定理和塞瓦定理,该定理亦可逆向用于判断三点共线,如下所述:
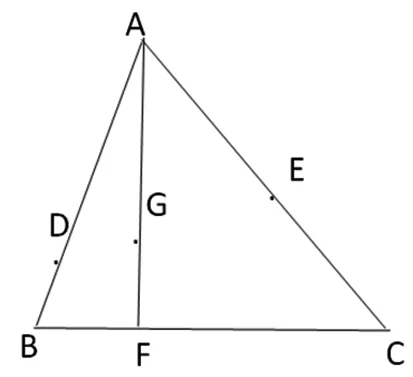
图14


证明过程可用“同一法”,即连接D、E交直线AF于点G′,证明G′与G重合即可,过程略.
猜你喜欢
中等数学(2022年7期)2022-10-24
中学数学研究(江西)(2022年5期)2022-05-08
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
中学数学研究(江西)(2021年8期)2021-09-06
中学生数理化(高中版.高二数学)(2021年3期)2021-06-09
中学生数理化(高中版.高二数学)(2021年2期)2021-03-19
小猕猴智力画刊(2016年5期)2016-05-14
福建中学数学(2013年1期)2013-03-06
中学数学研究(2008年3期)2008-12-09

