一道质检解析几何题的探究*——以2020年福建省高三质检理科第19题为例

福建省漳州市第三中学 (363000) 吴 攀

1.分析试题，探究解法

试题以椭圆为载体证明线段长度相等，题目包含了直线与圆锥曲线的位置关系等基础知识.考查推理论证能力，运算求解能力，以及数形结合，化归与转化，函数与方程等思想；要求考生具有直观想象，逻辑推理，数学运算等核心素养.

本题要求学生通过代数运算解决几何问题，要求学生会通过合理引参表示出直线，合理假设直线在一定程度上会减少运算量，能根据几何关系合理转化也是处理解析几何问题的常用手段，解析几何试题可以培养学生的运算能力，要求学生懂得合理的选择算法算理，掌握恰当的运算策略解决问题，以提高学生的数学运算核心素养．

2.解题反思，拓展延伸

在试题讲评的过程中，我们常常引导学生做解题反思：题目数据改一改，还会吗？题目的结论是否具有一般性，能不能推广？条件和结论对调，还能不能成立？基于以上反思，我们得到以下变式：

点评：问题的本质没有改变．因为l1为椭圆的右准线，考虑将直线l2移至过右焦点F，通过改变数据，发现结论仍然成立．

进一步，我们自然会提出问题：对于任意给定的椭圆，直线l2过椭圆的焦点F，直线l1为椭圆的准线，点D是否为线段MG的中点？

下面给出这个结论的一种简便证明方法.

图1

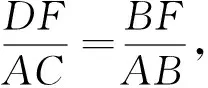
通过以上证明我们得到结论：

结论1 过椭圆的焦点F的直线l与椭圆交于两点A,B，过点A做F相应准线的垂线，垂足为C，若此准线与椭圆对称轴交于点G，则直线BC与x轴的交点D必为线段FG的中点．

连接AB′，同理可证得DF=DG，所以A,D,B′三点共线，从而得到结论2.

结论2 过椭圆的焦点F的直线l与椭圆交于A,B两点，过点A,B分别做F相应准线的垂线，垂足为C，B′，则直线BC与AB′的交点必为线段FG的中点．

我们进一步探究，以上结论在双曲线和抛物线中是否成立？利用变式2同样的证法，我们得到以上结论在双曲线和抛物线中同样成立，于是我们得到一个统一结论.

结论3 圆锥曲线的焦点弦的端点在相应准线上的投影与另一端点的交叉连线的焦点必过定点，且定点平分焦点与准线和对称轴的交点连线段.