一道数量积问题的多视角求解

秦波华

(浙江省湖州市第五中学，313000)

试题对平面内单位向量e1,e2,e3,u=(e2-e1)·(e2-e3) 的取值范围是______.

视角1坐标法

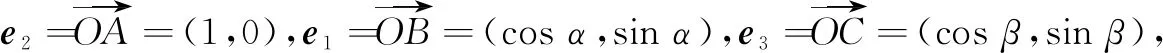
评注由圆的参数方程引入参数,将向

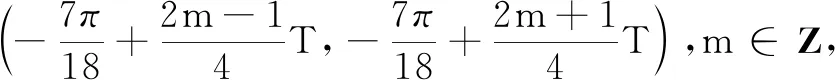
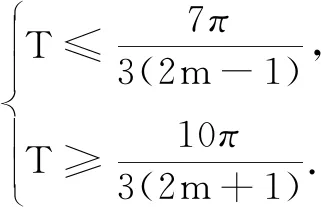
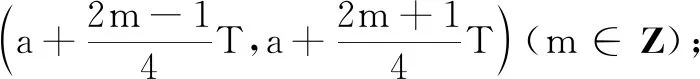
量问题转化为三角最值问题，但由于表达式比较繁琐，对运算能力要求比较高.

视角2不等式法

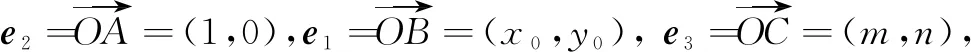
评注柯西不等式是处理多变量最值的一种有效的方式.本解法将解析法与柯西不等式结合,体现了代数法解决几何问题的优势,要求学生具备一定的综合分析处理问题的能力.

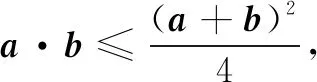
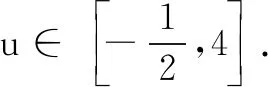
评注本解法用向量基本不等式解题,利用整体与局部的关系简化了代数计算的难度,对抽象思维提出了较高要求.

视角3定义法

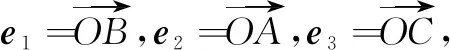
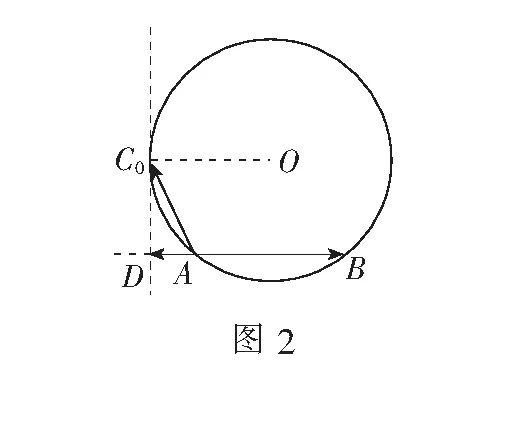
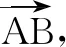
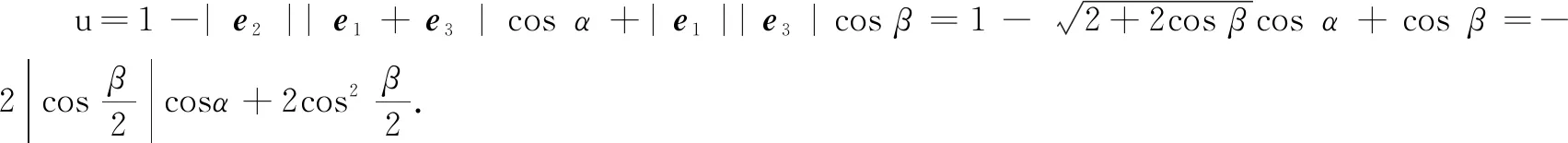
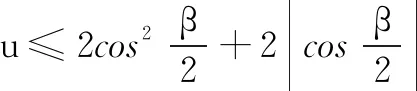
评注本题其实是一个多元动点问题.解法4、解法5表明解题时要遵循其处理原则:动变定,先定后动.

视角4极化恒等式法

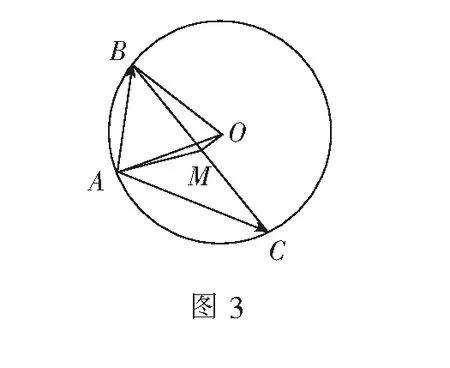
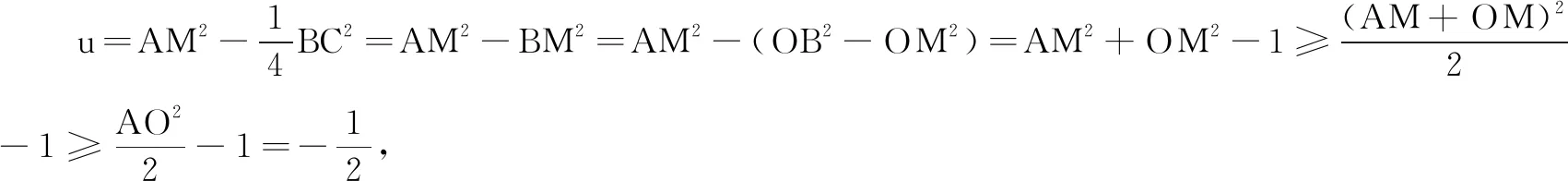
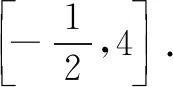
评注极化恒等式是数形结合求解向量问题的重要解题方法.本解法通过先固定点A，从极化恒等式的角度将问题转化为求AM2+OM2-1最小值的问题,后续的基本不等式和折线变直线都是本方法的亮点.

视角5解三角形法

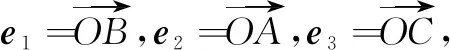
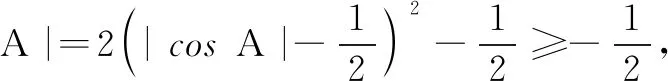
评注本探究利用数量积的定义转化为三角形中的边角关系,而单位圆是三角形的外接圆,因此，用正弦定理就顺理成章了.

视角6配方法

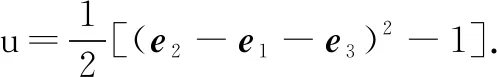
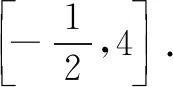
评注关注初高中重要知识点的衔接,注意新旧知识的联系,由u的表达式联想平方公式,解题过程干净利落.

解决数学问题重在探索解决问题的思维过程,弄清基本数学方法和基本数学思想是解问题的关键.运用不同的思维方法解决同一个数学问题有多种途径,重视知识的迁移,强化对知识深层次理解并做到综合运用,需要我们在创造性的学习过程中不断归纳和总结,学会站在高处看问题.