把握问题本质 发展核心素养*

唐昌荣 杨佳林

(贵州省实验中学，555003)

解析几何是高中数学的重要内容,其中定点、定值问题看似特殊实则具有一般性,解题时把握住这类命题的本质，多角度探索,并对特殊性与一般性进行拓展研究,可以有的放矢地实现高效复习,提升学生数学思维,进而发展学生的数学核心素养.本文以今年高考全国I卷理科数学第20题为例进行分析.

一、试题呈现

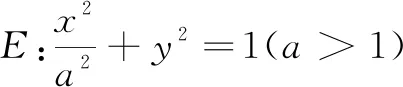
(1)求E的方程;

(2)证明:直线CD过定点.

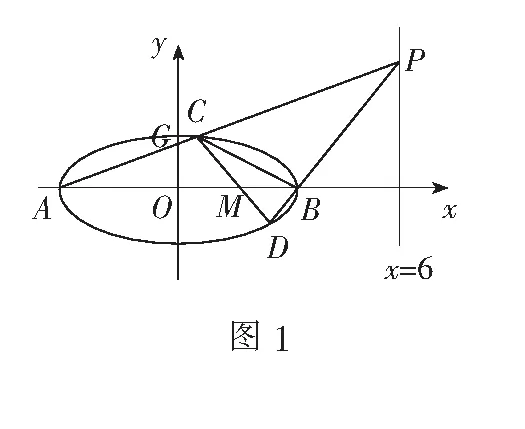
二、多视角探究问题本质

视角1筑牢基础,把握通法

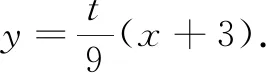
如图1,根据对称性,可知定点在x轴上,设为M(x0,0).

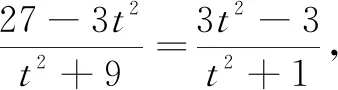
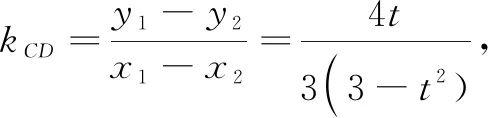
评析本解法属于通法,通过设点、联立直线与椭圆方程,借助韦达定理用t表示出C,D的坐标,最后根据C,D的坐标求出直线方程,使问题获解.优点是容易入手,缺点是计算量大、对运算素养要求较高.

视角2设而不求,整体处理

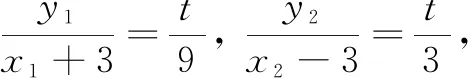
①

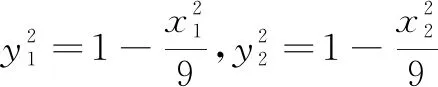
②

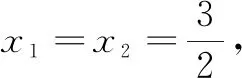
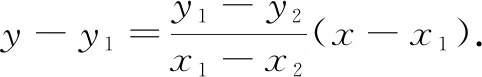
评析本解法通过设点法,先由斜率关系消去参数t,得到① 式;再根据点C,D在椭圆上,通过整体代入得到② 式;最后利用对称性可求出x轴上定点,充分体现了解析几何“设而不求,整体运算”思想的运用,简化了运算,提升了学生逻辑推理与数学抽象等核心素养.

视角3巧用对称,轻车熟路

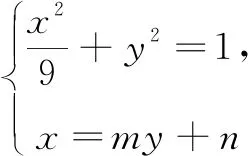
③

2my1y2+3(n-3)y1=(n+3)y2,将③ 式代入,整理得(2n-3)(n-3)y1=(2n-3)(n+3)y2,

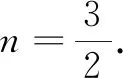
评注本解法巧设直线CD方程为x=my+n,轻车熟路,在同解法2得出2my1y2+3(n-3)y1=(n+3)y2的基础上,通过联立直线与椭圆的方程得出③ 式,再由③ 式代入得到关于y1,y2的一次对称式,具有计算量小、思维量也不大的特点,笔者认为属于最优解法,值得推荐.

视角4平移变换、齐次构造

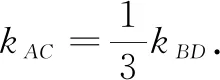
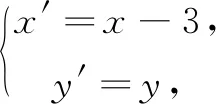
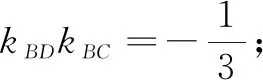
视角5伸缩变换,曲径通幽

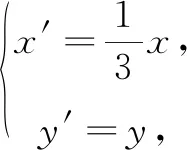
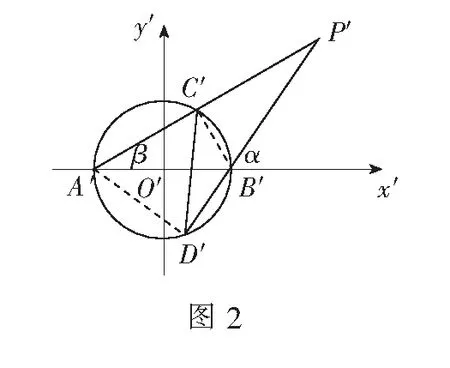
在新坐标系下,设点P′(2,t),∠P′B′E′=α,∠P′A′E′=β,则A′B′=2,B′E′=1,P′E′=t,且tanα=3tanβ.所以,在Rt∆A′B′C′与Rt∆A′B′D′中,A′C′=2cosβ,B′D′=2cosα.

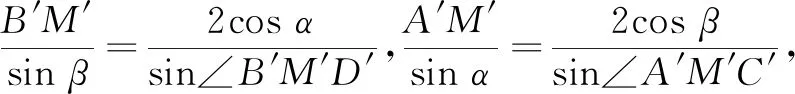
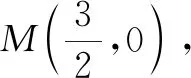
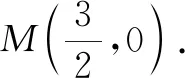
仿上述探究,不难得到如下推论(限于篇幅,证明留给读者).

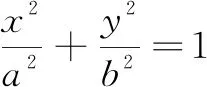
推论3P为直线x=-m(m>0)上任意一动点，直线OP交抛物线y2=2px(p>0)于另一点Q，点R在抛物线上，且PR平行于x轴，则直线QR过定点(m,0).