高一数学测试

一、单项选择题(本大题共8小题,每小题5分,计40分)

1.函数f(x)的定义域为(1,+∞),则f(2x+1)的定义域是 ( )

(A)[3,+∞) (B)(3,+∞)

(C)(0,+∞) (D)(1,+∞)

2.设函数f(x)=2x+3,g(x+2)=f(x),则g(x)的表达式是 ( )

(A)2x+1 (B)2x-1

(C)2x-3 (D)2x+7

3.f(x)与g(x)表示同一函数的是 ( )

(B)f(x)=1,g(x)=(x-1)0

4.已知A={1,x,y},B={1,x2,2y},若A=B,则x-y=( )

5.设集合A={x|x>a2},B={x|x<3a-2},若A∩B=∅,则a的取值范围为 ( )

(A) (1,2)

(B) (-∞,1)∪(2,+∞)

(C) [1,2]

(D) (-∞,1]∪[2,+∞)

6.函数y=f(x)的图象与y轴的交点个数为 ( )

(A)至少一个 (B)至多一个

(C)必有一个 (D)一个或无穷多个

二、多项选择题(本大题共4小题，每小题5分，计20分)

9.全集U={1,2,3,4,5},集合S={1,2,3,4},则US⊇( )

(A) {5} (B){1,2,5}

(C){2,3,4} (D)∅

10.下列图象中,可表示函数图象的是 ( )

(A)-1 (B) 3 (C) 2 (D)1

(A)有最大值1 (B)最小值-1

(C)无最小值 (D)无最大值

三、填空题(本大题共4小题，每小题5分，计20分)

13.已知集合A={a-2,2a2+5a,12},且-3∈A,则a的值为______.

14.若函数y=f(x)的定义域是[2,4],则函数g(x)=f(x-1)的定义域是______.

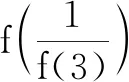
四、解答题(本大题共6小题，计70分.解答时应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)函数f(x)的图象如图所示,曲线BCD为抛物线的一部分.

(1)求f(x)的解析式;

(2)若f(x)=1,求x的值.

18.(本小题满分10分)已知函数

求f(g(x))和g(f(x))的解析式.

19.(本小题满分12分)某市居民自来水收费标准如下:每户每月用水量不超过25吨时,按每吨3.2元收费;当每户每月用水量超过25吨时,其中25吨按每吨3.2元收费,超过25吨的部分按每吨4.80元收费．设每户每月用水量为x吨,应交水费y元.

(1)求y关于x的函数关系;

(2)某用户1月份用水量为30吨,则1月份应交水费多少元;

(3)若甲、乙两用户1月份用水量之比为5∶3,共交水费228.8元,分别求出甲、乙两用户该月的用水量和水费.

20.(本小题满分12分)若A={x|x2-3x+2=0}B={x|x2+2(a+1)x+(a2-5)=0}.

(1)若A∩B={2},求实数a的值;

(2)若A∪B=A,求实数a的取值范围;

(3)若U=R,A∩(UB)=A,求实数a的取值范围.

21.(本小题满分12分)已知一次函数f(x)为增函数,且f[f(x)]=4x+9,g(x)=mx+m+3(m∈R).

(1)当x∈[-1,2]时,若不等式g(x)>0恒成立,求m的取值范围；

22.(本小题满分14分)是否存在实数a，使f(x)=x2-2ax+a的定义域为[-1,1],值域为[-2,2]?若存在,求出a的值;若不存在,请说明理由．

参考答案

一、单项选择题

1.C；2.B;3.D;4.C;5.D;6.B;

7.D;8.D.

二、多项选择题

9.AD;10.ACD;11.AC;12.AC.

三、填空题

四、解答题

17.(1)当-1≤x≤0时，函数图象为直线且过点(-1，0)，(0，3),其斜率为k=3,方程为y=3x+3.

当0≤x≤3时,函数图象为抛物线,设函数解析式为y=a(x-1)(x-3),由y(0)=3，得3a=3,a=1,故y=(x-1)(x-3)=x2-4x+3.

18.当x≥0时,g(x)=x2,f(g(x))=2x2-1；当x<0时,g(x)=-1,f(g(x))=-3.所以

19.(1)由题意,可得

(2)当x=30时,水费为y=80+4.8(30-25)=104(元).

(3)设甲、乙两用户1月份用水量分别为5m,3m.

若m≤5,则甲、乙两用户共交水费8m×3.2≤128元,不合题意.

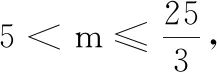
答:甲用户用水量为40吨,交费152元；乙用户用水量为24吨,交费76.8元.

20.(1)由A∩B={2},得2∈B.代入B中方程得a2+4a+3=0,解得a=-1或a=-3.

当a=-1时,B={-2,2},满足条件；当a=-3时,B={2},也满足条件.

综上，a=-1或a=-3.

(2)由A∪B=A,得B⊆A.

当Δ=4(a+1)2-4(a2-5)=8(a+3)<0,即a<-3时，B=∅,满足条件.

当Δ=8(a+3)=0,即a=-3时，B={2},满足条件.

当Δ=8(a+3)>0,即a>-3时，B=A={1,2}才能满足条件,此时a∈∅.

综上，实数a的取值范围为a≤-3.

(3)由A∩(UB)=A,A⊆(UB),得A∩B=∅.

当Δ<0,即a<-3时，B=∅,满足条件.

当Δ=0,即a=-3时，B={2},A∩B={2}不适合条件.

(2)由f(g(x))=2mx+(2m+9),g(f(x))=2mx+(4m+3),结合f(g(x))=g(f(x))，得2m+9=4m+3,解得m=3.故g(x)=3x+6.

当t=0时,φ(t)min=-1，得h(x)的值域为[-1,+∞).

22.f(x)=x2-2ax+a=(x-a)+a-a2,对称轴x=a.

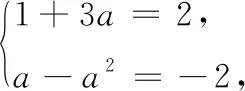
当a<-1时,由题意得f(x)在[-1,1]单调增.故f(x)的值域为[1+3a,1-a],有1+3a=-2，且1-a=2，满足条件的a不存在．

综上,存在a=-1满足条件．