零质量Kirchhoff型方程基态解的存在性
李安然, 樊丹丹
(山西大学 数学科学学院, 山西 太原 030006)
Kirchhoff方程
是由 Kirchhoff[1]在非线性振动理论中首次提出的一类非局部问题,用来描述物理学中可伸缩绳横向振动所引起的长度变化的现象.它是经典D’Alembert 弹性弦自由振动波动方程的推广.自从Lions在1978年提出了这个问题的抽象框架之后,各类Kirchhoff型方程在大量的文献中得到了广泛的研究[2-11]. 特别地,文献[11]应用单调性技巧和变分方法得到了带有零质量Kirchhoff型方程正解的存在性.零质量椭圆问题是指在一般的Schrödinger方程
-Δu+V(x)u=g(x,u),x∈m(1)
中V(x)≡0.文献[12]应用变分方法研究如下形式的零质量椭圆问题:
其中m是自然数且m≥3,K满足条件:
(K1) 存在k0>0使得
K(x)≥k0,x∈m.
(K2) 存在一个正的连续周期函数Kp:m→,即
Kp(x+y)=Kp(x),x∈m,y∈m.
使得
(K3)K是一个几乎处处为正的函数,即,
{x∈m:K(x)≤0}=0.
(K4)K∈L∞(m),对每个m中具有有界Lebesgue测度的Borel集序列{En},对n∈一致有
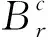
(g3)D(s)=sg(s)-2G(s)关于|s|单调递增且D(0)=0.
当条件(K1)、(K2)、(g1)~(g3)或(K3)、(K4)、(g1)~(g3)分别成立时,式(2)有一个正基态解.
1 主要结果
式中:λ>0;1 (f3)H(s)=sf(s)-4F(s)关于|s|单调递增且H(0)=0, (f4) 存在常数μ>4,使得 0<μF(s)≤f(s)s,s∈{0}; K满足文献[12]中的条件(K3)和(K4);a满足条件 (a1)a是几乎处处为正的函数, 主要结果是: 定理1 假设条件(f1)~(f3)、(K3)、(K4)、(a1)和(a2)成立,则对任意给定的λ>0,对每个q∈(4,6),式(3)有一个基态解; 注1 类似于文献[11-12,15],如果我们也要求f满足:当t≤0 时,f(t)=0,那么我们得到的式(3)的解也是正的.当q∈(1,4)时,式(3)是一类经典的凹凸非线性问题;当q>4时,式(3)在某种程度上可以看成经典临界问题的一个补充. 本文使用了以下约定和符号: ① 在大多数积分中,省略了符号“dx”; ③C,C1,C2,…表示正的常数; ④ 用un⇀u和un→u表示弱收敛和强收敛. 本文的主要工作空间: D1,2(3):={u∈L6(3):|u|∈L2(3)} 是一个Hilbert空间, 是其相应的范数.记Iλ:D1,2(3)→是式(3)对应的能量泛函,其具体形式如下: 由条件(f1)、(a1)和(a2)可知在Iλ在D1,2(3)上有定义,Iλ∈C1(D1,2(3),),并且对任意的u,v∈D1,2(3), 在本章中,证明在定理1的条件下,式(3)有一个基态解.首先,证明泛函Iλ满足山路几何结构,即引理1成立. 引理1 在定理1的条件下,泛函Iλ满足山路几何结构: (ⅰ) 存在βλ,ρλ>0使得对所有满足‖u‖=ρλ的u∈D1,2(3),有Iλ(u)≥βλ; (ⅱ) 存在eλ∈D1,2(3)满足‖eλ‖>ρλ,且Iλ(eλ)<0. 证明 由(f1)条件可知存在C>0,使得 又因为q∈(4,6),所以当‖u‖足够小时,Iλ(u)>0,即(ⅰ)成立. 取定u0∈D1,2(3){0}且u0(x)≥0, 显然当t→∞ 时,Iλ(tu0)→-∞,取充分大的tλ>0,使得‖tλu0‖>ρλ,且Iλ(tλu0)<0.(ⅱ)也成立. 因此,根据文献[16]可知,存在序列{un}∈D1,2(3)使得 式中, 这个序列被称为Iλ在cλ处的Cerami序列,简称(ce)cλ序列[17]. 接下来证明上述(ce)cλ序列{un}是有界的.首先有 引理2 当t∈[0,1] 时,存在常数Mλ>0使得对每个n∈,都有Iλ(tun)≤Mλ. 证明 令tn∈[0,1]使得 因为K(x)>0,a.e.x∈3, (f3) 意味着0≤H(t)≤H(1),t∈[0,1].所以可以得到以下估计: 又因为当n→∞时,Iλ(un)→cλ,所以它是有界的. 其次可以证明 引理3 上述(ce)cλ序列{un}在D1,2(3)中有界. 证明 用反证法证明这个结论.假设{un} 在D1,2(3)中无界,即当n→∞ 时,‖un‖→∞.令 则‖wn‖=1,故存在w∈D1,2(3)使得wn⇀w.接下来用反证法证明w=0.令Ω∶={x∈3:w(x)≠0},假设|Ω|>0,将Iλ(un)除以‖un‖4可得 由条件(f2)和Fatou’s引理可知 这是一个矛盾, 因此w=0. 下面证明 (5) 由条件(f1)可知,对任意的ε>0,存在常数s0>0和Cε>0使得 |F(s)|≤ε|s|6+Cεχ{|s|≥s0}(s).(6) 令 Fn={x∈3:Awn≥s0}, 则 其中C0>0且对所有的u∈D1,2(3)有 从而 由条件(K4)可知,对上述的ε>0,存在G>0,当r>G时,对任意的n∈一致有 即对任意给定的r>G, 对任意的n∈一致有 此外, 条件(f1) 也意味着 式中p∈[2,6).对上述给定的r>G,我们断言 事实上, 因为在D1,2(3)中wn⇀0,故在(3)中wn→0.即对上述的ε>0,存在N0>0 使得对每个n>N0,都有 因此由式(7)可知对每个n>N0, 因此 即式(5)成立. 故由式(4)可知,对每个给定的A>0, 当A足够大时,这与引理2矛盾,因此{un}有界. 定理1的证明 由引理3知{un} 有界,故存在u∈D1,2(3)使得un⇀u.要证明定理1,只需证明un→u,n→∞. 证明的关键是 和 首先证明式(8)成立.类似式(6),条件(f1)也意味着 定义 En={x∈3:un≥s0}, 则 其中C1>0使得 因此, 从而由式(10)可知 条件(K4)意味着对上述的ε>0,存在G>0,当r>G时,对任意的n∈一致有 故 类似于式(7),条件(f1)意味着 其中p∈[2,6).下面证明对每个r>0, 为此,定义截断函数 其中δ∈+是充分小的数,M∈+是充分大的数.令 则 因此, 因此, 即式(12)成立.从而式(8)也成立. 接下来证明式(9)成立.由条件(f1)可知,存在C>0,使得 因为{un}在D1,2(3)中有界,所以{f(un)}在3)中有界.又因为在L6(3)中un⇀u,故存在子列(不妨仍记为{un})使得un(x)→u(x),a.e.x∈3,从而f(un(x))→f(u(x)), a.e.x∈3.进而可知在3)中f(un)⇀f(u).又因为K∈L∞(3),所以Ku∈L6(3), 即式(9)成立. 根据弱收敛的定义,条件(a1)和(a2)意味着 和 所以结合式(8)、式(9)、式(14)和式(15)可得 因为D1,2(3)是一个Hilbert空间,所以在D1,2(3)中un→u.进而u是式(3)的一个非平凡弱解.此外,根据文献[17],条件(f3)和q>4意味着 因此,u是式(3)的一个基态解. 此时f满足条件(f1)和(f4),q∈(1,4],λ∈+是一个足够小的正数.首先,证明泛函Iλ满足山路几何结构,即引理4成立. 引理4 存在λq>0使得对每个λ∈(0,λq), (ⅱ) 存在e∈D1,2(3),使得‖e‖>ρ且Iλ(e)<0. 证明 (ⅰ) 由Sobolev不等式和条件(f1)可知 当t→∞ 时,Iλ(tu0)→-∞.故可取T0>0使得‖T0u0‖>ρ且Iλ(T0u0)<0. 当λ∈(0,λq)时,应用山路定理[18]可知,存在一个序列{un}∈D1,2(3)使得 式中, 这个序列被称为Iλ在能量水平cλ处的Palais-Smale序列,简称(PS)cλ序列. 引理5 (PS)cλ序列{un} 在D1,2(3)中有界. 当q∈(1,4) 时,很明显有{un}在D1,2(3)中有界,当q=4 时,选取同样可得{un}在D1,2(3)中有界. 定理2的证明 记 un→u,n→∞. 事实上,因为式(8)、式(9)、式(14)和式(15)成立,所以类似地可以证明 因此在D1,2(3)中un→u.继而u是式(3)的一个非平凡弱解. 也就是说{un} 是泛函Iλ的一个(PS)mλ序列.重复引理5的证明可得{un}是有界的,进而类似上述可以证明Iλ满足(PS)mλ条件,可知存在u∈D1,2(3)满足:Iλ(u)=mλ和即当时,式(3)有一个基态解. 本文利用变分方法和山路定理分别研究q和拟临界增长的连续函数f在2种情况下的零质量Kirchhoff型方程基态解的存在性.当q∈(4,6)时,我们用一般的方法证明了式(3)基态解的存在性,当q∈(1,4]时,我们通过构造基态能量的Palais-Smale序列,证明了式(3)基态解的存在性.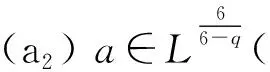
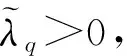

2 研究问题的变分框架
3 定理1的证明
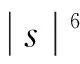
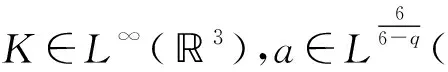

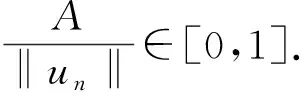
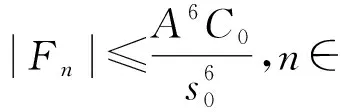
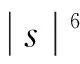


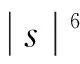
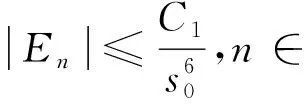
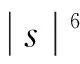
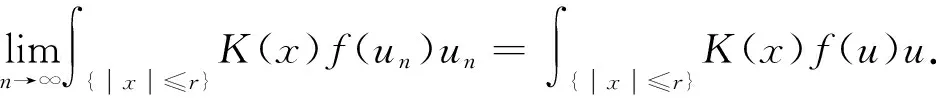
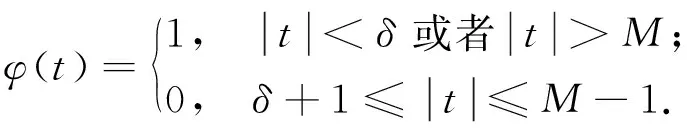
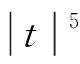
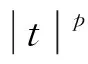
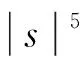
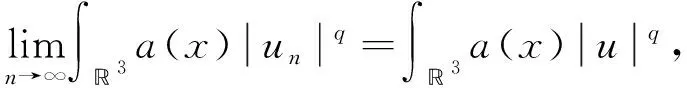
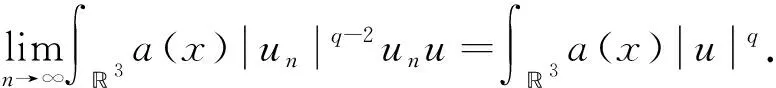
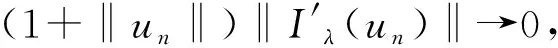
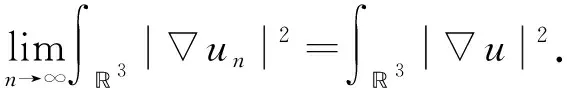
4 定理2的证明
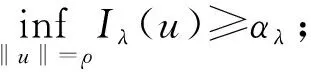
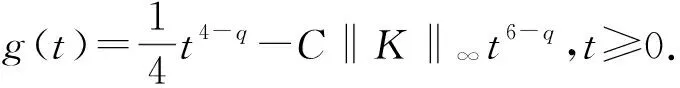
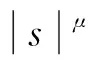
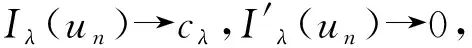
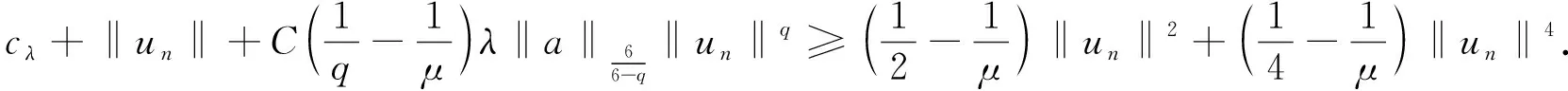
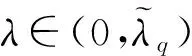
5 结 论

