基于人口流动因素的艾滋病传播微分方程模型

王跃华, 刘 娟, 扈 文

(1. 沈阳大学 师范学院, 辽宁 沈阳 110041;2. 辽宁师范大学 数学学院, 辽宁 大连 116029)

通过建立艾滋病传播的微分方程模型来研究该病的传播规律是预防和控制艾滋病的理论基础.对于微分方程[1]方面的研究已经吸引了各国学者的广泛关注并已经取得了较多的研究成果.用数学模型[2]和计算机来研究艾滋病传播机理可为控制政策的制定提供非常重要的思路[3].

对于这项问题的研究,有很多学者做出了贡献.龚道远等[4]从窗口期、无症状潜伏期、有症状期以及艾滋病后期4个阶段入手,建立了SWEIA艾滋病毒模型.陈雪玲[5]将男女分开考虑,研究异性和同性(男男)间的性接触对艾滋病传播的影响.王晓红等[6]建立了一个具有现实分布的数学模型,即将潜伏期划分为n个阶段.对于一个一般的具有双线性发生率的n阶段的阶段进程模型,研究了其动力学行为.王楚雯等[7]通过建立的最优模型对艾滋病确诊数及死亡率进行了预测分析.

通过对以上文献进行分析发现,现有艾滋病传播模型,很少考虑到人口流动对艾滋病传播的影响,而事实上,我国每年流动人口规模很大,人口流动对于艾滋病传播具有较大的作用.所以本文结合人口流动和地区差异对中国各地区按发病率高低进行分类,分为人口流动性低的地区与人口流动性高的地区,通过建立具有人口流动因素的艾滋病微分方程模型,研究艾滋病传播规律,为制定控制人口流动计划提供理论基础.

1 基于人口流动因素的艾滋病微分方程模型

在传统的传染病模型中有SI模型,这个模型适用于只有易感者和患病者2类人群,且不会反复发作的疾病,这与艾滋病很相似,下面简单介绍SI模型.

SI模型的假设条件如下.

1) 传播过程中总人数N为常数.令s(t)、i(t)分别代表t时刻易感染者和已感染者占N的比例;

2)λ表示日接触率,为常数.

1.1 假设

1) 假设艾滋病毒携带者和艾滋病患者不生育子女(母婴传播在传播途径中所占比例很小,这里忽略不计).

2) 假设艾滋病患者不会被治愈(虽然全球已经有2名被治愈的艾滋病患者,但其治疗策略不是一种可以大范围推广的策略).

3) 假设未来几年内艾滋病治疗成功率维持在90%(艾滋病病死率稳定在当前数据保持不变).

1.2 模型建立

由假设可建立如下微分方程:

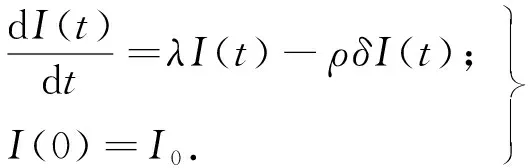
式中:I(t)表示t时刻艾滋病病毒感染者人数;λ表示日接触率;ρ表示因艾滋病死亡的人数占艾滋病病人总数的比例;δ表示艾滋病病毒感染者向艾滋病患者转变的比例;λ、ρ、δ是常数,只含有一个未知函数I(t).

下面对式(1)进行求解.分离变量得

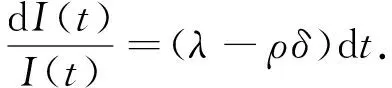
对式(2)两边积分得

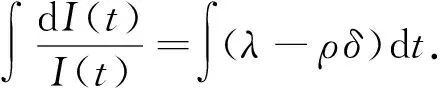
得到式(1)的通解为

I(t)=ce(λ-ρ δ)t.(4)

从中国疾病预防控制中心公共卫生科学数据中心查询到国内1985—2017年艾滋病感染者(HIV)人数和艾滋病患者(AIDS)人数,见表1.

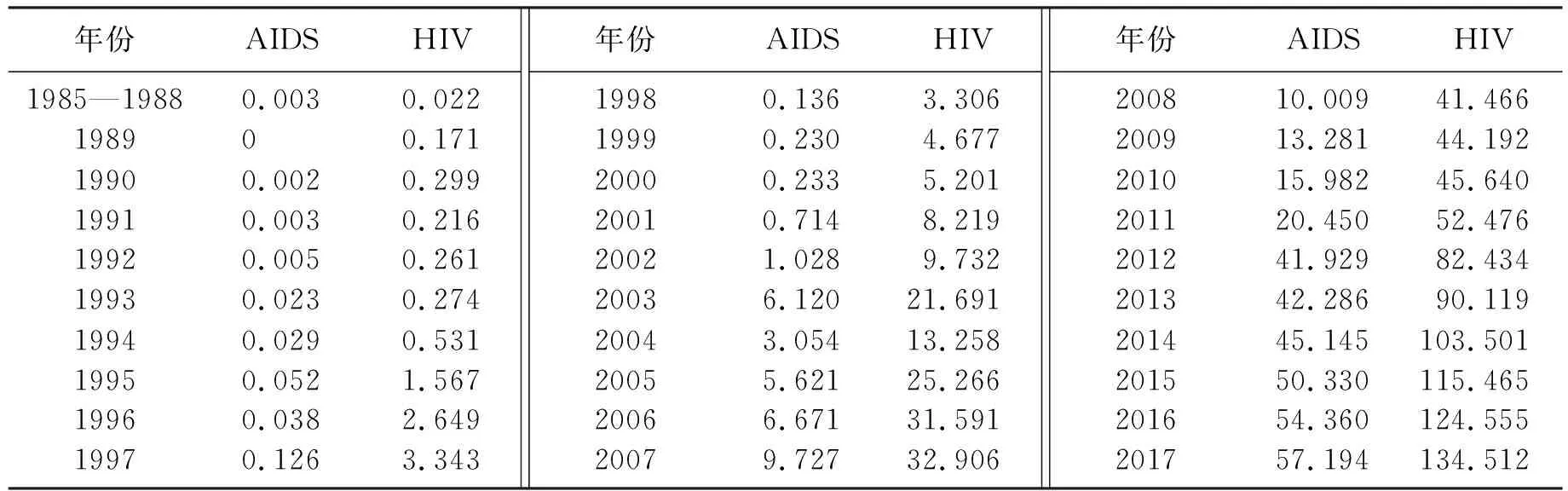
表1 1985—2017年中国艾滋病感染者人数和艾滋病患者人数[8]Table 1 The number of people infected with HIV and AIDS from 1985-2017 in China[8] 千人

根据表1中的数据,以1990年的数据为初值,即I(t0)=I0,I0=0.299,t0=1 990.根据微分方程的通解式(4)可得

I(t)=0.299e(λ-ρ δ)(t -1 990).(5)

式(5)就是式(1)的特解,下一步要确定参数δ、ρ、λ的值.

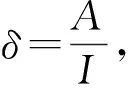
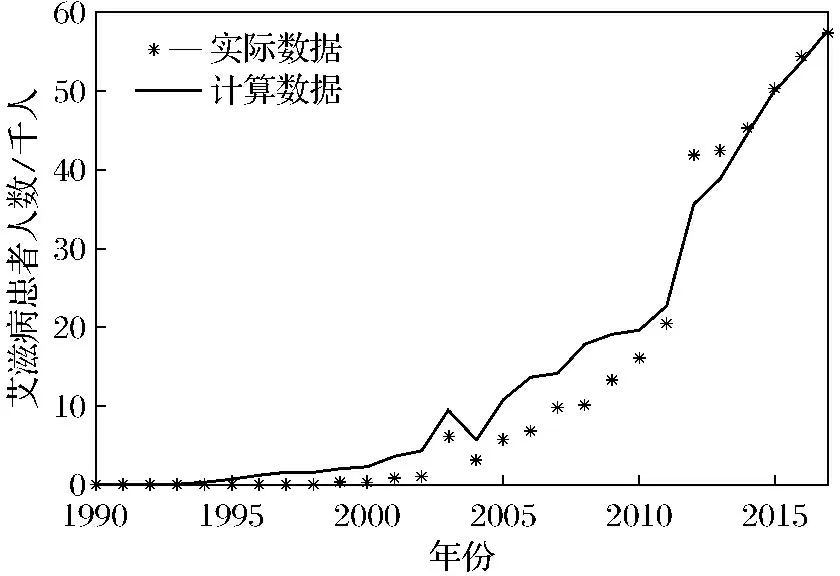
图1 1990—2017年艾滋病患者人数与A=δI计算的数据对比Fig.1 Comparison between the number of people infected with HIV and the data obtained byA=δI from 1990-2017

可以看出δ=0.43时,A=δI基本符合实际数据.

从中国疾病预防控制中心性病艾滋病预防控制中心查询到历年艾滋病发病人数和死亡人数,从而计算病死率,见表2.

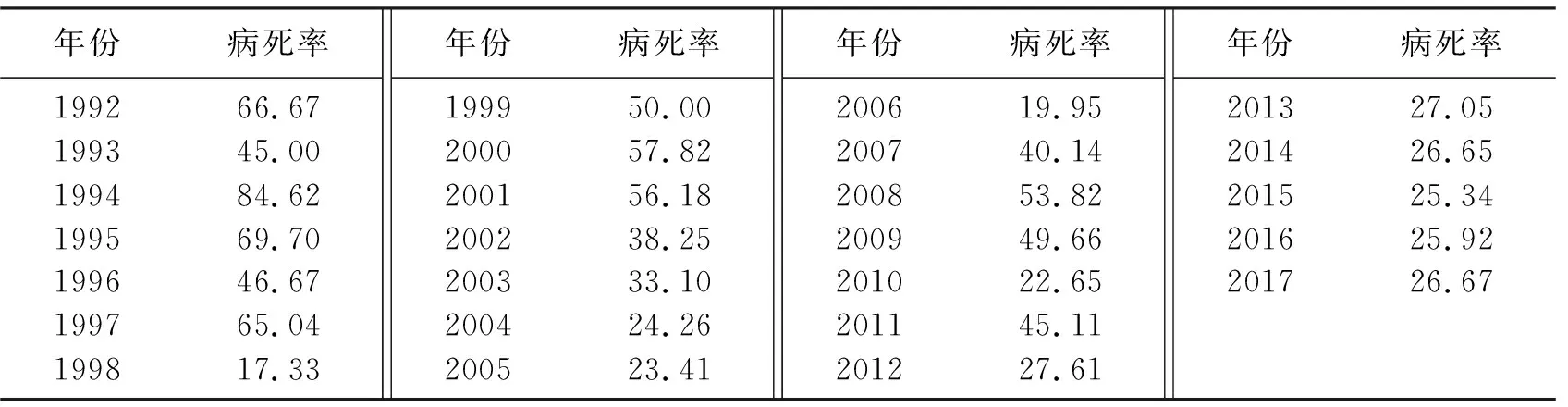
表2 1992—2017年中国艾滋病病死率[8]Table 2 The mortality of AIDS from 1992-2017 in China[8] %

接着,确定参数ρ的值.可以看出ρ的值分布散乱,无法求出具体值.但在近几年中,由于国家政策的支持、医疗水平的提高使艾滋病的治疗成功率达到90%,因此艾滋病的病死率维持在低水平.故可以取ρ=0.292 7.

接下来将δ与ρ代入式(5)得,

I(t)=0.299e(λ - 0.125 9)(t -1 990)(6)

设γ=λ-0.125 9,代入式(6)得

I(t)=0.299eγ(t - 1 990),(7)

则

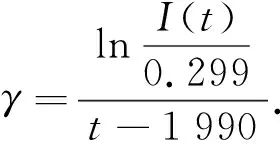
最后通过MATLAB求出γ的值,取γ=0.22,画出由I(t)=0.299eγ(t-1 990)得到的值与实际数据的比较图,见图2.

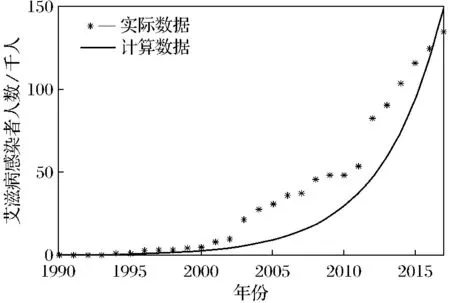
图2 1990—2017年艾滋病患者人数与由I(t)=0.299eγ(t-1 990)得到的值Fig.2 Comparison between the number of people infected with HIV with the value obtained byI(t)=0.299eγ(t-1 990) from 1990-2017

可以看出,取γ=0.22时,函数I(t)=0.299eγ(t-1 990)基本符合真实数据,能在一定程度上反映真实情况.

但是,在全国范围内,各个地区艾滋病患者数量不同,且一些发达地区的流动人口规模很大,所以要考虑人口流动、地区差异对艾滋病传播的影响,故需要对上述模型进行修正.利用前面的模型,将中国各地区按发病率高低进行分类,分为高发病率地区与低发病率地区.

补充假设:

1) 假设只在高发病率地区与低发病率地区之间发生人口流动;

2) 假设艾滋病患者人群由于受到限制不迁移.

修正模型:

由假设可建立方程

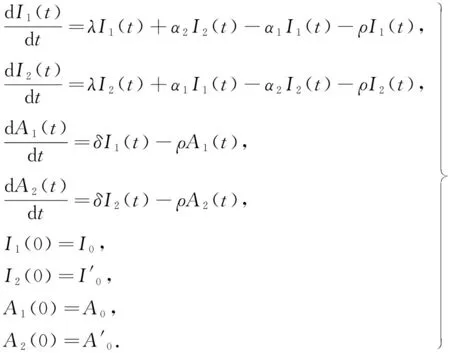
式中:I1(t)表示t时刻高发病率地区艾滋病病毒感染者人数;I2(t)表示t时刻低发病率地区艾滋病病毒感染者人数;A1(t)表示t时刻高发病率地区艾滋病患者人数;A2(t)表示t时刻低发病率地区艾滋病患者人数;α1表示高发病率地区人口迁出率;α2表示低发病率地区人口迁出率.

1.3 求解

1) 式(9)正解的存在性、唯一性和稳定性.

① 由式(9),令

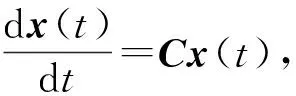
2) 式(9)的数值模拟.

由原始模型的求解可得,δ=0.43,ρ=0.292 7,λ=0.345 9.通过查询数据得到α1、α2的值,α1=0.011 54、α2=0.015 40.代入式(9)中得

从中国疾病预防控制中心公共卫生科学数据中心查询到中国2004—2016年高发病率地区与低发病率地区艾滋病病人数,见表3.

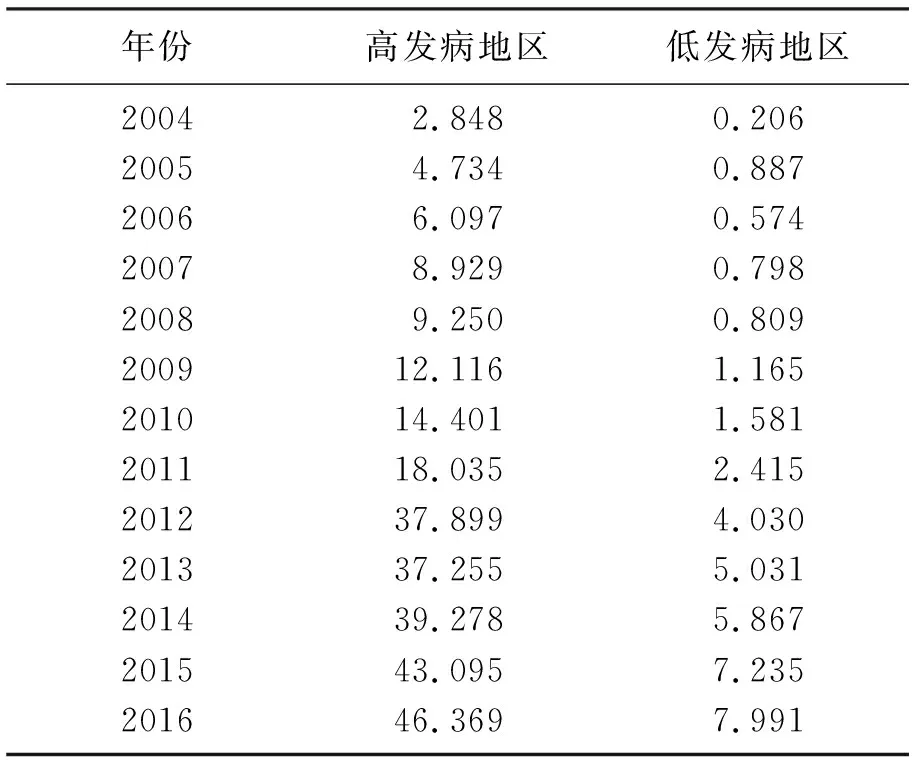
表3 2004—2016年中国高发病率地区与低发病率地区艾滋病患者人数[8]Table 3 The number of AIDS patients in high incidence rate areas and low incidence rate areas from 2004-2016 in China[8] 千人

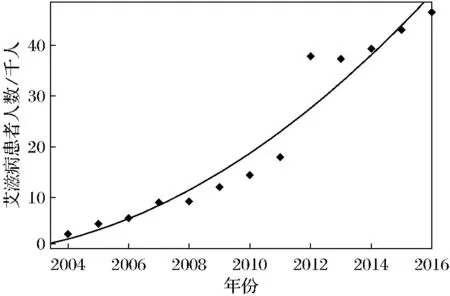
图3 由数据拟合得到的A1(t)曲线Fig.3 Curve of A1(t) obtained by data fitting

拟合函数表达式为

A1(t)=3.058t2+15.7t+18.74.

对A2(t)进行拟合,得到图4.

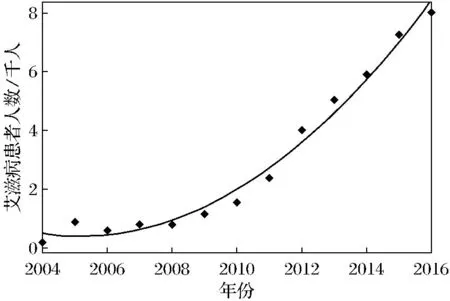
图4 由数据拟合得到的A2(t)曲线Fig.4 Curve of A2(t) obtained by data fitting

拟合函数表达式为

A2(t)=1.033t2-2.568t+2.015.

通过MATLAB计算方程组

的确，二乐的聪明和机智有好几次都让古意起了疑心。有一次，当我照常把二乐抱上餐桌吃饭时，他就颇不以为然地皱着眉头说：“古乐，我觉得你并不适合长期同一只狗生活在一起。”

(11)

的解析解,可以得到图5.

图5 两类地区艾滋病感染者人数的解析值Fig.5 Analytical value of the number of people infected with AIDS in two types of areas

可以看出在2004—2016年两类地区艾滋病毒感染者人数均在不断增加,但是增长速度有所不同,高发病率地区的感染速度远远高于低发病率地区.

1.4 分析

1) 对式(1)进行分析.

① 在方程I(t)=0.299e(λ-ρ δ)(t-1 990)中,λ越大,函数值I就越大.也就是说,每个病人每天有效接触的人数越多,艾滋病感染者人数越多.这是显然的.

②ρ越小,函数值I越大.即艾滋病病毒感染者人数,随着艾滋病死亡率的降低会越多.但是,这种情况不是一直发展下去的,因为艾滋病病人的死亡,会使得艾滋病病毒感染者的总数减少.

2) 对式(9)进行分析.

① 在方程

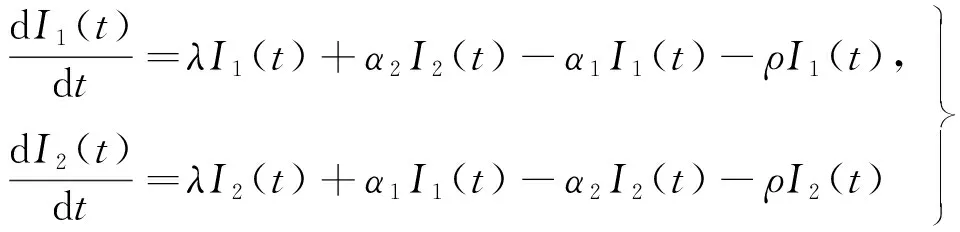
中减小α1、α2的值,其中α1=0.008、α2=0.01,可以得到图6.

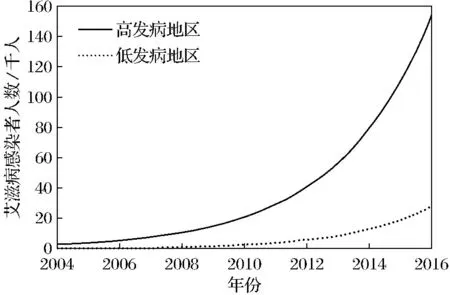
图6 迁出率对两类地区艾滋病感染者人数的不同影响Fig.6 The different influence of emigration rate on the number of people infected with HIV in the two areas

通过与图5对比可以看出,人口迁出率越小,可使艾滋病感染者人数越少.从而可以通过控制城市的人口迁出率,来控制艾滋病的传播.

② 由式(1)计算出2016年的艾滋病感染者人数和艾滋病患者人数如下,I(t)=81 167,A(t)=39 202.通过式(9)可以计算出2016年相应的艾滋病感染者及艾滋病患者人数:I1(t)=70 465、I2(t)=16 322、A1(t)=50 191、A2(t)=8 423,与表1的真实数据对比可以发现,式(9)比式(1)更加接近真实数据,这是由于式(9)中加入了人口流动因素,所以比式(1)更加接近真实情况.

③ 式(9)与文献[4]艾滋病传播模型主要的区别在于,文献[4]考虑到了传播模型的随机性,而式(9)通过人口流动,将中国各地区按发病率高低进行分类,分为高发病率地区与低发病率地区,建立了艾滋病传播的微分方程模型.

2 模型预测

利用拟合函数A1(t)=3.058t2+15.7t+18.74、A2(t)=1.033t2-2.568t+2.015和式(1)的解析解,通过MATLAB求解,对2020—2024年我国两类地区艾滋病患者人数及艾滋病病毒感染者人数进行预测.如表4.

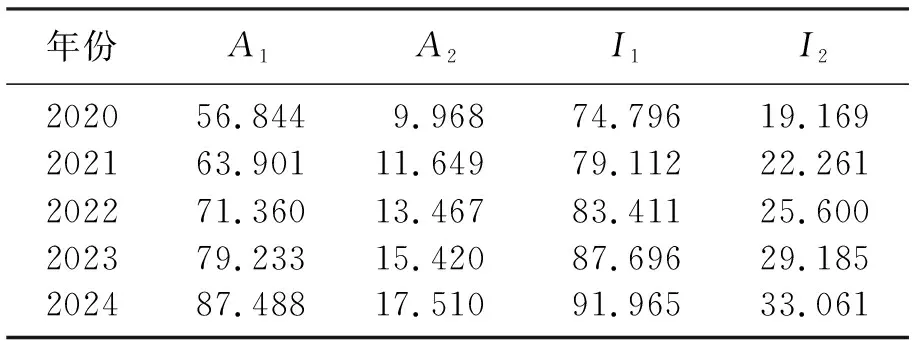
表4 两类地区艾滋病患者人数及艾滋病病毒感染者人数预测Table 4 The prediction of the number of AIDS patients and people infected with HIV in two regions 千人

可以看出,如果考虑到人口流动因素,情况是不容乐观的.今后5年里两类地区艾滋病病人数和艾滋病病毒感染者人数还将继续增长,而且增长速度较快.

3 结论与建议

通过以上模型分析可以看出跨省、跨地区的人口流动对艾滋病的传播影响很大,所以需要政府和个人的积极配合才能有效抗击艾滋病. 除了一些基本的防艾措施,如加强安全知识宣传和教育、道德教育等,也应注意有效控制艾滋病病毒感染者的人口流动.所以需要政府和个人的积极配合才能有效抗击艾滋病.

第一,有效控制艾滋病病毒感染者的人口流动.主要通过相关部门的有效监控及防范,加大监管力度.一方面,不间断进行艾滋病检测,增强防艾意识,提高艾滋病知晓率,以减少艾滋病携带者在不知情的情况下造成的艾滋病传播.同时,制定相关的有效政策,以减少相关艾滋病患者的频繁流动.

第二,加强安全知识宣传和教育.防艾工作从青少年抓起.主要表现为青少年对于艾滋病知识的认识相对薄弱,没有引起足够的重视,很多时候羞于提到这个话题.

第三,加强精神文明建设.一方面,增强自身的自爱意识,通过自身意识的清醒来做到严于律己;另一方面,改变大众对于艾滋病人的看法,引导民众积极、健康的价值观,做到不歧视艾滋病人,关心、帮助艾滋病人,营造良好的社会氛围.

第四,加强道德教育.对于艾滋病人,要时时关爱,以防范有的患者的不健康心理的产生,并对社会造成的不良影响.可以建立艾滋病交流中心,病人之间可以相互交流病情,减少压力,放松心情,在保护病人隐私的前提下对患者进行心理和生理的治疗.