一类具有分级感染率的时滞SEIR蠕虫病毒传播模型Hopf分岔

张子振, 邹俊宸, 门秀萍

(安徽财经大学 管理科学与工程学院, 安徽 蚌埠 233030)

随着互联网应用的日益增多和新信息技术的出现,蠕虫病毒已经成为我们工作和日常生活中的一大威胁,造成了巨大的经济损失.尤其是物联网的快速发展将使蠕虫病毒对人类社会的威胁日益严重.根据FreeBuf提供的2019年度上半年网络安全态势报告统计,2019上半年在全国监测到蠕虫病毒样本共计20 451个,共拦截9.48亿次;并且蠕虫病毒很难清理,尤其是政企单位易感染[1].因此,如何有效防御蠕虫病毒的攻击是网络用户面临的一个亟待解决的问题.近年来,基于传染病动力学原理,构建动力系统模型以了解蠕虫病毒在网络中的传播行为,并预测控制其在网络中的传播,引起了国内外研究学者的关注.

Feng等[2]提出了一类考虑网络拓扑结构的SIRS(susceptible infectious recovered susceptible)无线传感网络蠕虫病毒传播模型,并研究了模型的稳定性.考虑到蠕虫病毒的潜伏特性,Keshri等[3]提出了一类具有潜伏状态的时滞SEIR(susceptible exposed infectious recovered)无线传感网络蠕虫传播模型,并研究了模型Hopf分岔的存在性.Ojha等[4]提出了具有2类潜伏状态的SEIR网络蠕虫传播模型.SEIR模型假设恢复状态节点的免疫力是永久的,这显然与现实中的实际情况不相符.因为网络中会不断出现新的蠕虫病毒,并且反病毒软件的更新换代远不如新的蠕虫病毒出现的速度快.基于此,Guillen等[5-7]提出了不同形式的SEIRS(susceptible exposed infectious recovered susceptible)网络蠕虫传播模型.最近,考虑到网络中节点输入率和移出率的时变性和差异性,蔡秀梅等[8]提出了如下不同输入率和不同输出率的SEIR蠕虫病毒传播模型:

(1)

式中,S(t)、E(t)、I(t)和R(t)分别表示网络中易感节点、潜伏状态节点、感染节点和恢复状态节点在时刻t的数量.A表示进入网络中易感节点的速率;b为由于蠕虫病毒的攻击导致的感染节点断网率;c为所有节点的自然断网率;α为易感节点的感染率;δ、η、β和ε为各类节点之间的状态转移率.

蠕虫病毒的显著特征之一就在于其具有潜伏性. 即, 网络中的节点在t-τ时刻感染蠕虫病毒, 经过时间周期τ以后才会爆发具有感染性. 显然, 式(1)忽略了网络中蠕虫病毒的潜伏期. 其次, 式(1)假设潜伏状态的节点不具有感染性.而在现实的网络中, 潜伏状态的节点, 也可以通过文件下载或者文件复制等途径进行病毒的传播[9]. 此外, 时滞因素对动力系统的稳定性有着非常重要的影响, 甚至会使系统变得不稳定[10]. 基于以上考虑, 并受文献[11-12]研究工作启发, 本文研究如下具有分级感染率的时滞SEIR蠕虫病毒传播模型:

(2)

式中,τ为蠕虫病毒的潜伏期时滞;α1和α2分别为感染状态节点和潜伏状态节点的感染率.本文主要研究τ对式(2)稳定性的影响.

1 基本再生数和有病毒平衡点

令式(2)中的方程右边为0,即

(3)

进而,有

(4)

于是得到蠕虫病毒基本再生数

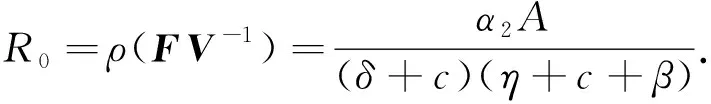
根据式(3)和基本再生数R0,可以得到式(2)的有病毒平衡点为P*(S*,E*,I*,R*).其中,

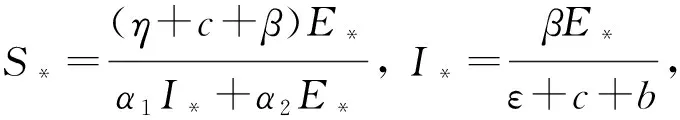
2 Hopf分岔的存在性

式(2)在有病毒平衡点为P*(S*,E*,I*,R*)处的雅克比矩阵为

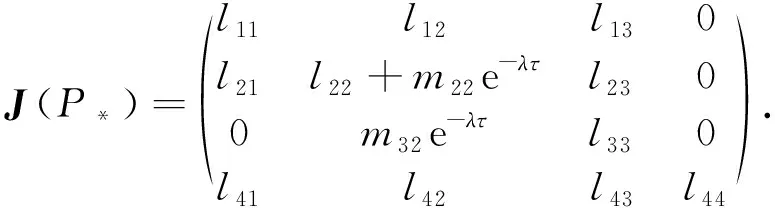
式中,

相应的特征方程为

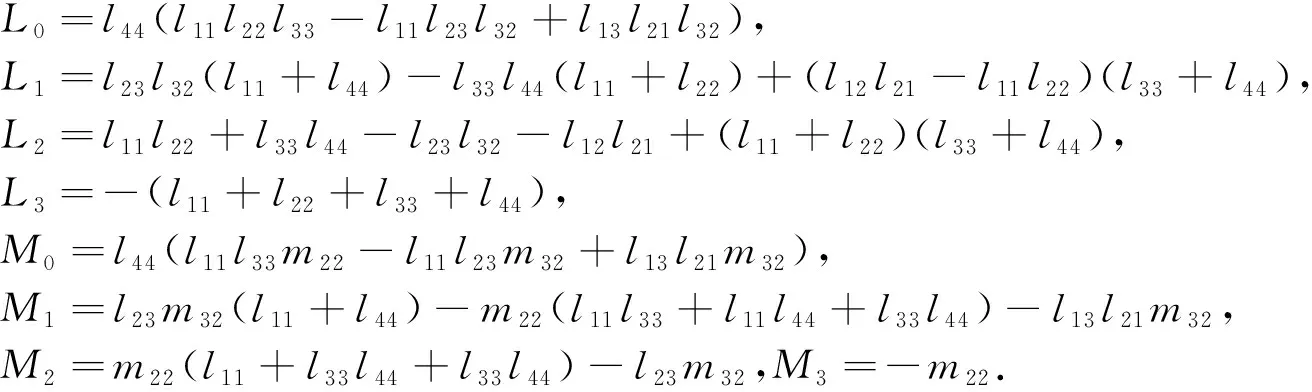
当τ=0时,式(7)变为

λ4+L13λ3+L12λ2+L11λ+L10=0.(8)

式中,L10=L0+M0,L11=L1+M1,L12=L2+M2,L13=L3+M3.

当τ>0时,令λ=iω(ω>0)为式(7)的根,则

因此,有

ω8+L23ω6+L22ω4+L21ω2+L20=0.(10)

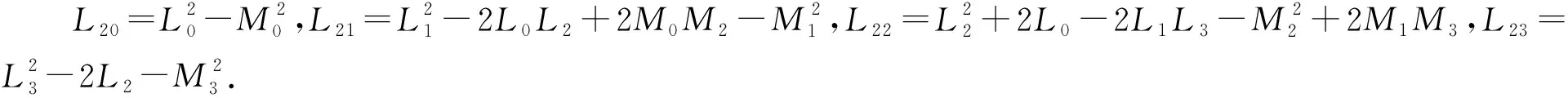
令ω2=ϖ. 那么式(10)可以变为

ϖ4+L23ϖ3+L22ϖ2+L21ϖ+L20=0.(11)

根据文献[15]关于四次代数方程式(11)根的分布情况讨论结果,给出下列假设(H2):式(11)至少存在一个正实根.

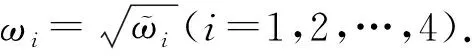
式中,

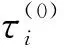
因此,有

式中,

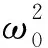
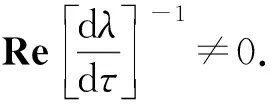
定理1 对于式(2),如果条件(H1)～(H3)成立,那么当τ∈[0,τ0)时,式(2)局部渐近稳定;当τ=τ0时,式(2)失去稳定并在有病毒平衡点P*(S*,E*,I*,R*)附件产生一簇分岔周期解.

仿真示例

选取A=2.1,δ=0.002,c=0.02,α1=0.006,α2=0.004,η=0.008,β=0.08,ε=0.007,b=0.01.式(2)的示例模型为

经过计算可以得到R0=3.535 4>1,进而得到示例模型式(12)的有病毒平衡点P*(6.363 1,18.148 3,39.239 5,21.629 4).从而有ω0=1.902 5,τ0=24.889 2.选取τ=23.287 5<τ0=24.889 2时,根据定理1可知,示例模型式(12)局部渐近稳定.仿真效果如图1所示.

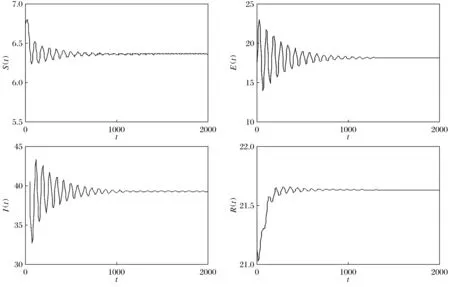
图1 当τ=23.287 5<τ0=24.889 2时,示例模型式(12)局部渐近稳定Fig.1 Example model (12) is locally asymptotically stable when τ=23.287 5<τ0=24.889 2

选取τ=26.758 5>τ0=24.889 2时,根据定理1可知,示例模型式(12)失去稳定并产生Hopf分岔,仿真效果如图2所示.

图2 当τ=26.758 5>τ0=24.889 2时,示例模型式(12)失去稳定并产生Hopf分岔Fig.2 Example model (12) loses stability and a Hopf bifurcation occurs when τ=26.758 5>τ0=24.889 2

3 结 论

本文在文献[8]的基础上,进一步考虑蠕虫病毒的潜伏期以及潜伏状态节点的感染能力,提出了一类潜伏状态节点和感染状态节点具有不同感染率的时滞SEIR蠕虫病毒传播模型.相比于文献[8]中所构建的蠕虫病毒传播模型,本文所研究的时滞SEIR模型更具有一般性.

以潜伏期时滞τ为分岔参数,通过分析模型特征方程根的分布情况,推导出模型局部渐近稳定和Hopf分岔存在的局部渐近稳定的充分条件,计算得到产生Hopf分岔的时滞临界点τ0.研究结果表明,当时滞τ的取值低于τ0时,模型处于理想的局部渐近稳定状态.此时,有利于蠕虫病毒的传播控制.一旦时滞τ的取值高于τ0,模型将失去稳定并在有病毒平衡点附近产生一簇分岔周期解.此时,蠕虫病毒的传播将失去控制.因此,对于本文研究的SEIR模型,应该尽可能控制或者消除Hopf分岔的产生,以便有效控制蠕虫病毒的传播.