一道教师解题能力展示试题的赏析
广东佛山顺德罗定邦中学(528300) 李定平
1 题目
2018 佛山青年教师解题能力展示试题第16 题:设函数f(x)=−x2+bx+|x −a|−a −1,(a,b ∈R),若对∀a ∈R,函数f(x)至多有两个不同的零点,则b的取值范围是____.
姑且不论难易得分如何? 此题中既是分段函数,又含有两个参数a和b,而且还有对任意参数a命题成立求参数b范围的恒成立问题,是一个综合性较强的题,引起笔者的探索.
2 解法呈现
思维视角1讨论f(x)的单调区间,由零点个数确定的区间端点的正负求b范围.
解法1等价于对∀a ∈R,f(x) =x2−bx −|x −a|+至多有两个不同的零点,而f(x)是两个开口向上,对称轴分别为和的分段二次函数.


图1

图2
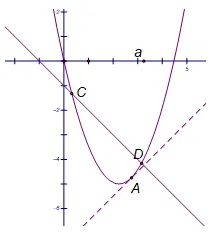
图3
思维视角2函数零点转化为二次函数与分段函数的交点,由分段交点个数求b范围
解法2等价于对∀a ∈R,关于x的方程

至多有两个不同的解, 即h(x) =x2−bx g(x) =至多有两个不同的的交点,而g(x)的图像是顶点为P(a,−a −1),斜率分别为1 和−1 的折线,其中左侧是l:y=−x −1,右侧是m:y=x −2a −1.
当l与h(x)无交点时, 即x2−(b −1)x+1 = 0 无实数解,即∆= (b −1)2−4<0 得:−1< b <3 时,右折线m:y=x −2a −1 与h(x)最多两交点,方程1○至多有两个不同的解;
当l与h(x) 有一个交点, 即b= 3 或b= 1 时, 右折线m与h(x)可能存在两个交点,如b= 3 时,当a= 0 时,x2−3x=x −2a −1 存在两个大于a的解,方程1○有三解,不满足要求.
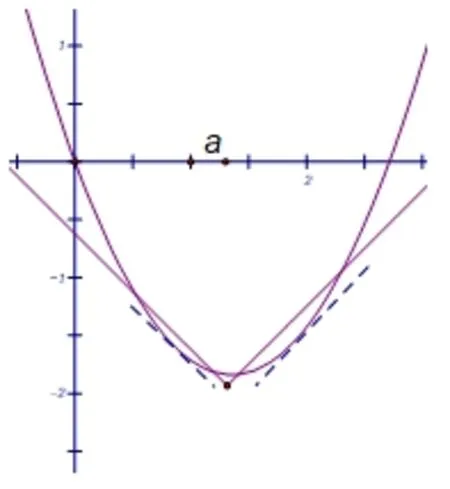
当l与h(x)有两个交点时(如图3),作h(x)的斜率为1 的切线n, 记切点为A, 若A在直线l的上方时, 存在右折线m也与h(x)有两个不同交点,故g(x)与h(x)有4 交点,方程1○有4 解,不满足要求; 若A在直线l的下方或在直线l上时,g(x)与h(x)至多有2 交点,满足要求,设切线n:y=x+c,代入y=x2−bx得:x2−(b+1)x −c= 0,所以即b2−2b −7 ≥0,解得或此时满足要求.
综上所述,略.
思维视角3函数零点转化为一个含参数a的函数与参数b表示常数函数的交点,由交点个数求b范围
解法3等价于对∀a ∈R,关于x的方程
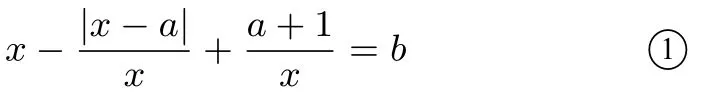
至多有两个不同的解,即等价于h(x) =与y=b至多有两个不同的的交点, 而p(x) =x −1 +, 当2a+ 1>0 时与一样是对钩函数, 当2a+ 1<0 时是(−∞,0)与(0,+∞)都单增的两段增函数.
(1)当a≤−1 时,q(x)在(−∞,a]上单增,p(x)在(a,0)上单增,在(0,+∞)上单增,h(x)与y=b至多有两个不同的的交点,则b ∈R(如图4);
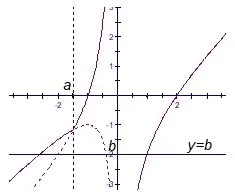
图4
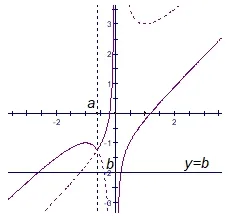
图5
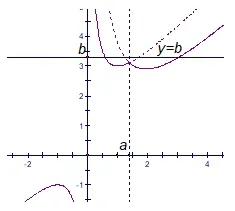
图6
因为对∀a ∈R,至多只有两个交点,所以上述所求b范围取交集即为所求.
评析这种化归观察交点个数最为明显.
思维视角4求补集:∃a ∈R,f(x)至少有三个不同的零点,求b的取值范围.
解法4由h(x) =x2−(b −1)x+1(x≤a)有两零点x1 由g(x) =x2−(b+ 1)x+ 2a+ 1(x > a) 有两零点a ∃a ∈使式成立,即 ∃a ∈使式成立,即 评析注意“∃a ∈使式成立”的运算. 思维视角5求补集:化归为∃a ∈R,含参数b的抛物线与含参数a的折线至少有三个不同的交点,求b的取值范围. 图7 解法5由f(x) = 0 变形为x2−bx=|x −a|−a −1,令h(x) =x2−bx,g(x) =|x −a|−a −1,h(x)与g(x)至少有三个交点(如图7),则h(a)≥g(a),即 评析V 型折线与抛物线至少有三个交点当且仅当V 型顶点在两切点之间且在抛物线下方,两切点在折线下方. 函数的零点可转化为两函数的交点,对∀a ∈R,则要想象参数a任意变化,相应的函数图象如何变化,对直观想象能力要求较高,分界点x=a变化导致函数图形变化主要靠想象,不仅优秀学生需要这样的训练,作为教师也需要. 函数零点问题大部分是含一个参数,象这样含两个参数的题较少,如2015 湖南卷理第15 题:已知f(x)=若存在实数b,使函数g(x) =f(x)−b有两个零点,则a的取值范围是____.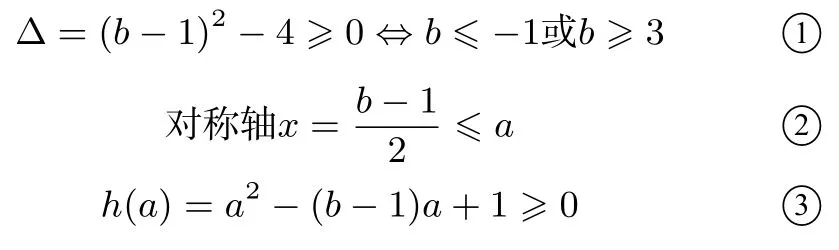
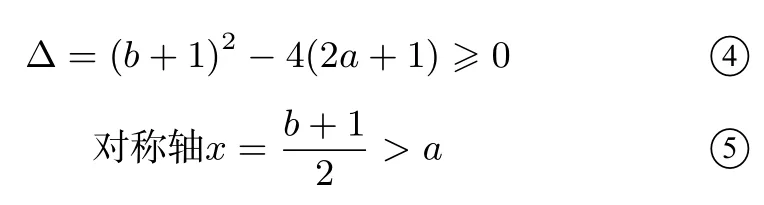
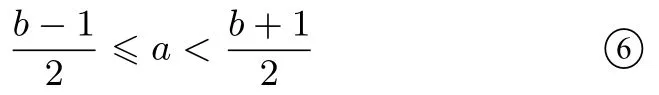
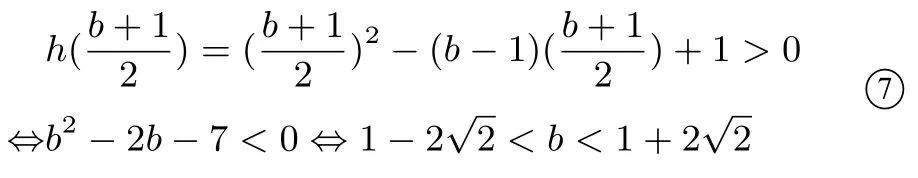


3 感想

