在中小学数学衔接的教学中发展学生的思维*

江苏省张家港市第一中学(2156000) 展 学

从小学进入初中,总有部分学生小学时的成绩不错,然而进入中学就成绩明显下降, 两极分化的趋势越来越严重.这跟中小学的教学方式、学习方法、学习环境和学生心理等方面的变化有一定关系,但最主要的是跟学生的思维发展有关.人的思维发展有关键期,在不同的年龄阶段表现为不同的思维年龄特征,在不同的思维年龄阶段进行思维培养效果最好,反之将会事倍功半[1].弄清学生的思维发展特点,在中小学数学衔接的教学中应该根据学生思维的年龄特征进行针对性的培养.下面就中小学数学衔接的教学中如何发展学生的思维和广大同行们一起探讨.

1 从正数和零到有理数域,发展数学的知识结构,形成思维的逻辑体系

负数的引进是初中数学学习的开端,在这节课的学习中要让学生感受到为什么学习负数,这是解决实际问题的需要.负数存在怎么样的知识结构中,学生怎样才能将负数建构在自己原有的知识结构中.怎样去思考数集的扩展过程,才能形成和增强思维能力,为后续的无理数、虚数的引进积累经验.

案例1苏科版·数学七年级上册“2.1 正数与负数”的教学.

数的产生离不开生活,由记数产生了数1,2,3···,表示“没有”产生0,这就产生了自然数. 在自然数中进行“+”运算,还是自然数,进行“−”运算呢,必须是大数减小数,否则就会不够减.

问题1某地早晨8 点的温度是3°C,中午12 点温度上升了5°C,晚上9 点温度又下降了11°C,则中午和晚上的温度各是多少?

问题2零上3°C 和零下3°C 一样吗,如何区分呢?

图1 生活中的正负数

问题3观察图片,说出它们的实际含义,你能说出图中带有“−”号的数的表示的意思吗?

归纳总结像3、5、8848.43、100、357、78 这样的数叫做正数;像−3、−154、−38.87、−117.3 这样的数叫做负数.

“+”读作“正”, 正号通常省略不写;“−”读作“负”, 如“−117.3”读作“负一百一十七点三”,负号不能省略.

问题40°C 以上的温度用正数表示,0°C 以下的温度用负数表示.如何用正数和负数表示日常生活中意义相反的量呢?

例1(1)如果向北走8km 记作+8km,那么向南走5km记作什么?

(2)如果粮库运进粮食3t 记作+3t,那么−4t 表示什么?

思考:相反意义的量包括哪些方面?你能用正数和负数表示日常生活中具有相反意义的量?

问题5正数和负数可以表示具有相反意义的量,“0”既不是正数也不是负数,它也不再是小学中的表示“没有”的意义,而是作为一个基准出现,它是正数与负数的分界点.在正整数的前面加一个“−”号,就变成了负整数,在正分数的前面加一个“−”号,就变成了负分数. 正整数、负整数、零统称为整数.正分数、负分数统称为分数.整数和分数统称为有理数.这样,有理数按照定义来分类,可分为:

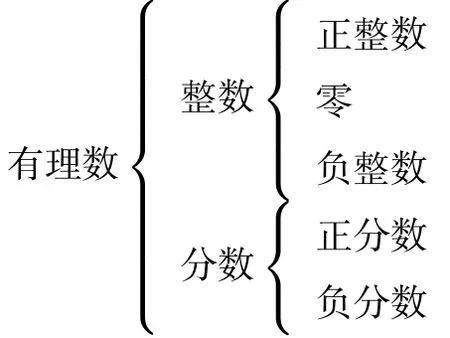
学习了负数后,数的范围从小学里的正数和零扩展到了有理数,有理数按照正负来分类,可分为:

设计意图负数的学习是中小学衔接教学的开端,问题1 是从实际生活入手,让学生感受引入负数的必要和学习负数的价值.问题2、3 让学生体会负数的表达方式,从具体情境中抽象出数学模型,让学生感受负数就在我们身边,体会“+”、“−”具有双重意义.问题4、5 让学生感受负数的出现是由于解决实际问题的需要而发展出来的,负数的出现使数的范围扩大了,通过用正负数来表示意义相反的量,0 不仅可以表示没有,还可以看成是正负数的分界点,让学生在原有正数和零的基础上感受数集的扩展,在原有算术数的基础上建构知识结构,形成有理数的结构体系,并在此基础上,积累思维经验,增强思维能力,形成思维的逻辑体系.

2 从算术到方程到方程组,选择不同的思考方式,培养应有的思维习惯

在解决实际问题时,小学里习惯把未知量置于一个特殊的位置,想方设法通过已知量去求未知量;中学里则把未知量和已知量放在同等的位置, 寻找等量关系建立方程求解.小学算术方法是逆推的思维,强调套用类型;方程解法是顺向推导,是顺向思维,两者本质上是思维方法的转变.

案例2苏科版·数学七年级下册“10.2 二元一次方程组”的教学[2].

问题1我国古代算书《孙子算经》有一题:

今有鸡兔同笼

上有三十五头

下有九十四足

问鸡兔各几何

分析古文翻译并研究:“上有三十五头”的意思是什么?“下有九十四足”呢?

问题2“今有牛五、羊二,直金十两,牛二、羊五,直金八两.牛羊各直金几何?”

题目大意是:5 头牛、2 只羊共价值10 两“金”,2 头牛、5只羊共价值8 两“金”.每头牛、每只羊各价值多少“金”?

设计意图问题1 在小学时学生是用算术方法去计算,初中则要求用一元一次方程解决,让学生感受小学里用算术方法计算是逆向思维,而列一元一次方程是把未知量用字母来表示,未知量、已知量在平等的位置上,设法找出等量关系,是顺向推导,逆向思维比较容易处理一些简单的方程,但对于复杂一点的方程,思维含量高时就比较困难,这时容易看出顺向推导的好处,体会方程的优越性.问题2 学生在用未知数表示另一个未知量的时候对思维的要求更高,这时就出现了困难,导致问题不能解决.尤其问题2 这类题目更加放大了这个问题,让学生感到设两个未知数就避免了这个矛盾,所以说设两个未知数很有必要,感受到了学习二元一次方程的必要性和价值.另外,也会从未知量的角度出发,发现设一个未知数就列一元一次方程,设两个未知数列出来的是方程组,经历不同的思考方式,利于对方程本质的理解,拓宽了思维的渠道,培养了数学应有的思维习惯.

3 从动手操作到逻辑推理,挖掘不同的思维表征,发展学生的思维层次

数学思维蕴含于数学材料之中,材料的不同表征对学生的思维有不同的影响.同一个问题不同的设计方式所导致学生的思维方式、思维参与程度也是完全不同的,从实践操作到论证推理,学生的思维层次是不一样的,中小学衔接教学对同样的内容应考虑不同的思维层级,促进学生的思维更高层次发展.

案例3苏科版·数学七年级下册“7.5 多边形的内角和与外角和”的教学.

问题1前面我们学习了三角形,三角形研究了边和角两种元素.对于边,我们知道三角形的任意两边之和大于第三边;对于角,你知道哪些结论?

三角形的内角和是180°.

问题2你们还记得小学时是如何验证“三角形的内角和是180°”的吗?

(1)量,用量角器量出三个角的度数再相加;(图2,(1))

(2)拼,撕下三个角拼在一起;(图2,(2)(3))

(3)折,通过折叠将三个角折在一起. (图2,(4))

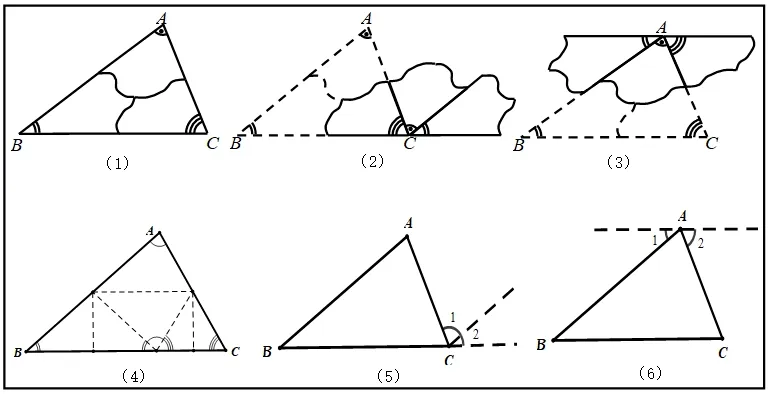
图2 三角形内角和验证方法

问题3上面的方法有什么共同的特点吗?

将三个角移动到一起,拼成一个平角.

问题4如果我们不量、不拼、不折,你能将三个角移动到一起吗?回忆一下前面学过的内容,哪些方法可以移动角的位置,还不改变角的大小呢?

添加平行线,构造三线八角.(图2,(5)(6))

你能根据刚才拼图的过程,添加平行线,用推理的方法说明“三角形的内角和是180°”吗?

设计意图问题1、2 是从学生的认知出发,回顾了小学里学的三角形内角和定理,通过量、拼、折等方法进行验证三角形的内角和是180°,这并不是严格的论证,而是利用特例,用不完全归纳的方法得到的结论.问题3、4 继续深入,将动手操作得出结论过渡到推理论证得出结论,学生结合拼图的方法,想到添加平行线,构造三线八角将角转移,从而证明三角形内角和定理.从思维的层次上看,前面两个问题主要是利用学生的具体形象思维,后面两个问题向辩证逻辑思维发展,将学生由小学的感性认识提升到理性认识,由动手操作发展到逻辑推理,培养学生演绎推理的能力,向更高层次的思维发展.

在课堂教学中, 我们要根据中小学数学知识的变化特点、学生思维的发展规律,把握中小学教学内容的内在联系,让教学内容的思维表征和思维特征统一,或者由同一教学内容的不同思维表征发展学生的思维层级,使学生的思维达到一定的高度,中小学数学的教学衔接工作自然就水到渠成了.