群的结构

梁 静

(安徽新华学院 通识教育部，安徽 合肥 230088)

0 引言

1 预备知识

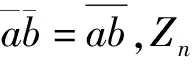
引理1 若p为素数，n>0，则φ(pn)=pn-1(p-1).

引理2 若(m,n)=1，则φ(mn)=φ(m)φ(n).

证明考查mn阶循环群Zmn，因(m,n)=1，故Zmn≌Zm⊕Zn.设a,b∈Zmn分别为m阶元和n阶元，则Zmn={aibj|1≤i≤m,1≤j≤n}，又aibj为mn阶元⟺ai,bj分别为m阶元和n阶元⟺(i,m)=1且(j,n)=1.满足等价关系左边的有序对(i,j)有φ(mn)对，满足等价关系右边的有序数对(i,j)有φ(m)φ(n)对，从而有φ(mn)=φ(m)φ(n).

证毕.

2 主要结果

证明1)显然.

下面为使叙述严谨将采用原根的语言法证明.

证明由上，取a为模p的一个原根，则(a+p)p-1-ap-1≡ap-1+p(p-1)ap-2-ap-1≡p(p-1)ap-2≠0(modp2).

由定理1和定理2即可得到:

由定理1、2、3可得如下结论：

3 结论