基于灰色马氏链模型的农村居民消费水平预测
屈 聪,王瑞柯,张水利
(平顶山学院 数学与统计学院,河南 平顶山 467036)
中国是一个农业大国,农村人口多且分布范围广,农村消费市场巨大.改革开放以来,我国经济不断发展,伴随着日益增长的生活水平,人们的消费水平也有了很大的提高.特别是进入21世纪以后,农村居民消费观念的改变使得消费总量进一步增加[1-3].对农村居民未来消费水平进行预测,有助于及时调整相关政策,优化消费环境.刘斌、张慧、白宏远等利用灰色关联方法对农村居民消费结构进行了分析和预测[4].屈聪、李宜懋利用灰色马氏链模型对农村居民收入进行研究,结果表明灰色马氏链模型预测的精度更高[5].笔者以全国2000—2018年的全国农村居民消费水平为样本数据,建立了灰色马氏链模型,并对2019—2025年全国农村居民消费水平进行了预测,获得了较好的结果.
1 灰色马氏链预测模型
1.1 灰色GM(1,1)预测模型
灰色预测是指对系统行为特征值的发展变化进行的预测,对既含有已知信息又含有不确定信息的系统进行的预测,也就是对在一定范围内变化的、与时间序列有关的灰过程进行预测.建立GM(1,1)模型的具体过程如下:
1)选取等时距连续的一组原始数据列:
(1)
2)对测量数据做一次累加,得到新的数据列:
(2)
3)采用一阶微分方程进行拟合,得到GM(1,1)模型:

(3)
式(3)中:
a——发展系数,
u——灰色作用量.
(4)
式子(4)是连续时间t的响应函数,对其进行离散化,得到微分方程的数值解如式(5)所示:
(5)
使用最小二乘法得到参数列如下所示:
(6)
于是可得到灰色预测的离散时间响应函数为:
(7)
x(1)(t+1)为所得的累加的预测值,将预测值还原即为
(8)
1.2 马氏链
若随机过程{X(n),n=0,1,2,…}只取有限或可列个值,并且对任意的n≥0,及任意状态i,j,i0,i1,…,in-1,有
P{Xn+1=j|Xn=i,Xn-1=in-1,…,X1=i1,X0=i0}=
P{Xn+1=j|Xn=i}.
(9)
则随机过程{X(n),n=0,1,2,…}称为Markov链.Xn=i表示过程在时刻n处于状态i,称{0,1,2,…}为该过程的状态空间,记为S0.对Markov链,给定过去的状态X0,X1,…,Xn-1及现在的状态Xn,将来的状态Xn+1的条件分布与过去的状态独立,只依赖于现在的状态.
1.3 马氏性检验
称(9)中的条件概率P{Xn+1=j|Xn=i}为Markov链{X(n),n=0,1,2,…}的一步转移概率,记为pij,表示处于状态i的过程下一步转移到状态j的概率,则转移概率矩阵为
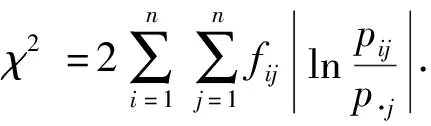
2 实证分析
利用2000—2018年农村居民消费水平数据,建立灰色马氏链模型,并进行预测.
2.1 GM(1,1)模型的验证
2.2 划分状态


表1 GM(1,1)预测值、残差序列及状态
2.3 检验马氏性
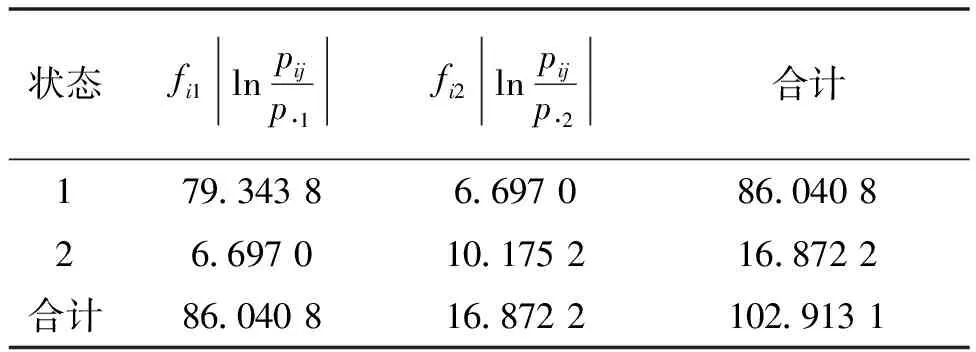
表2 卡方统计量
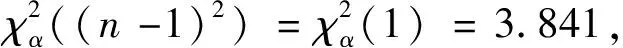
2.4 计算预测值
根据状态区间划分和灰色预测值,计算灰色马氏链模型的预测值.由于原始序列最后一个数据落在了状态1内,则初始矩阵为P(0)=(1,0).经计算发现未来处于状态1的概率大,因此得到预测值及相对误差,如表3所示.
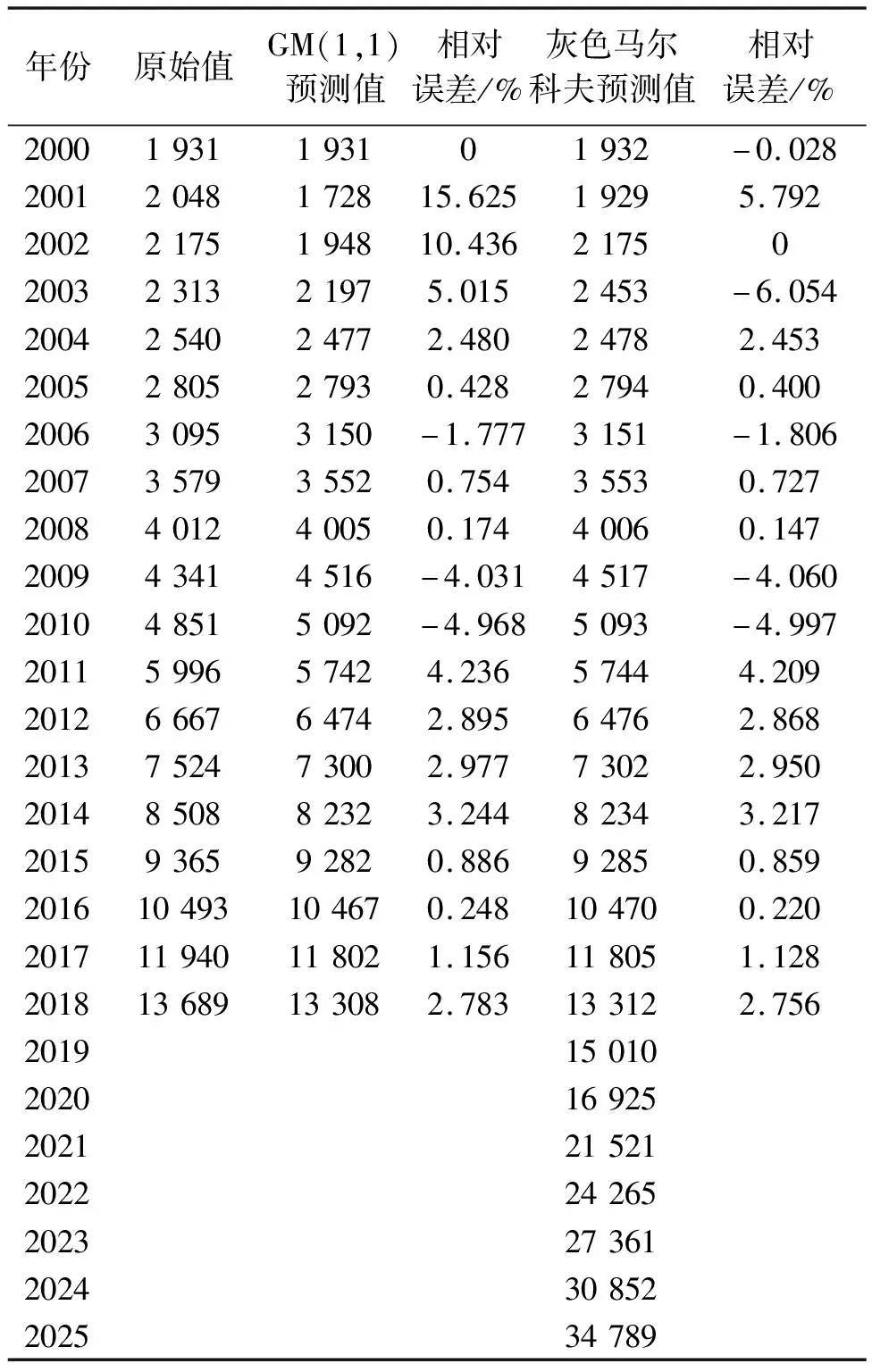
表3 灰色马尔科夫预测值及相对误差
从表3中可以看出GM(1,1)模型的相对误差绝对值的平均值为3.374%,灰色马氏链模型相对误差绝对值的平均值为2.351%,与GM(1,1)模型相比,预测精度提高了1.023%,因此利用灰色马氏链进行预测的效果更好.
3 结论
笔者运用灰色模型与马氏链相结合的方法对农村居民的消费水平进行了预测,用上述方法得出的预测值与真实值之间的误差较小,并且与灰色模型相比,此方法大大提高了预测精度,得到了较好的结果.
预测结果表明:我国农村居民消费水平仍处于上升趋势,可见随着国家经济的发展,农村居民的生活质量将逐步提升,生活水平会越来越高.
——基于指数增长模型

