基于主成分判别分析的全国主要城市空气质量评价

侯甜甜，户亚慈

(平顶山学院 数学与统计学院，河南 平顶山 467036)

0 引言

空气质量是人类生存环境的重要组成部分，良好的环境质量也是城市经济稳定增长和可持续发展的必要条件之一.随着社会经济的高速发展,城镇化水平不断提高，资源和能源大量消耗,机动车保有量迅速增加，大量有毒有害气体被排放到空气中，导致空气质量明显下降，已对人类赖以生存的生态环境系统造成了严重威胁.

中国大气污染状况十分严重,主要表现为煤烟型污染.城市大气中总悬浮颗粒物浓度普遍超标，二氧化硫污染一直在较高水平，机动车尾气污染物排放总量迅速增加，氮氧化物污染呈加重趋势.汽车是机动车大气污染排放的主要贡献者，是机动车污染防治的重中之重.国内外许多学者加大了对空气质量指标的研究，2008年冯梅、徐浙峰根据淮安市区的空气污染指标对空气质量状况进行评价,2014年王露云对2008—2012年间我国31个主要城市环境空气质量展开评价,2014年毛宁、李益禛[1]基于主成分对全国31个城市空气质量进行分析，得出空气质量污染主要来自于可吸入颗粒和二氧化硫，为控制大气中的污染指标提供支持.

1 预测方法

1.1 主成分分析模型

主成分分析[2]是对于原先提出的所有变量，将重复多余的变量(关系紧密的变量)删去，建立尽可能少的新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息.最经典的做法就是用F1(选取的第一个线性组合，即第一个综合指标)的方差来表达，即Var(F1)越大，表示F1包含的信息越多.因此在所有的线性组合中选取的应该是方差最大的，故称F1为第一主成分.如果第一主成分不足以代表原来p个指标的信息，再考虑选取F2,即选第二个线性组合，为了有效地反映原来信息，F1已有的信息就不需要再出现在F2中，用数学语言表达就是要求cov(F1,F2)=0，则称F2为第二主成分，依此类推可以构造出第三,第四，…，第p个主成分.方差越大提供的信息越充分.第一个主成分的方差最大，依次减少.模型如下：

Fp=a1i×Zx1+a2i×Zx2+…+api×Zxp.

其中,a1i,a2i,…,api(i=1,…,m)为X的协方差阵∑的特征值所对应的特征向量，Zx1,Zx2,…,Zxp是原始变量经过标准化处理的值，为了排除因变量的单位不同带来的影响，需要对数据进行标准化处理，这样数据具有可比性，所以在计算之前须先消除量纲的影响，将原始数据标准化，笔者所采用的数据就存在量纲影响.数据标准化是指Z标准化,R为相关系数矩阵,变量相关的系数矩阵R的特征根为λ1≥λ2≥…≥λp≥0,ai是特征值所对应的特征向量.A=(aij)p×m=(a1,a2,…,am)，Rai=λiai，进行主成分分析的主要步骤如下：

1)指标数据标准化；

2)确定主成分个数m,即F1,F2,…,Fm，根据研究问题，构建指标体系；

3)建立综合评价模型,即主成分Fi表达式；

4)根据主成分Fi的得分，进行排名.

1.2 费希尔(Fisher)判别

费希尔(Fisher)判别[2]是选择一个适当的投影轴，让多维数据使用投影数据压缩在一定方向,采用的是尽可能将总体与总体之间分开投影的原则.原来的坐标下,很难让样本独立,投影后可以明显地区别各总体.应用这个线性函数把p维空间中的已知类别总体以及求解类别样本都变换为一维数据，再根据其间的亲疏程度把未知归属的样本点判定其归属.这个线性函数应该能够在把p维空间中的所有点转化为一维数值之后，既能最大限度地缩小同类中各个样本点之间的差异，又能最大限度地扩大不同类别中各个样本点之间的差异，这样才可能获得较高的判别效率,即依据组间均方差与组内均方差之比最大的原则来进行判别.对于新样品的p个指标值,分别带入判别函数中求出值,从而对其进行分类.

…… ……

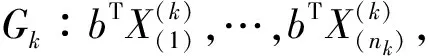
每个总体投影后均为一元数据，对k组数据做方差分析，组间平方和为

组内平方和为

φ(b)=bTBb-λ(bTEb-1),

解方程组得到

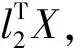
2 实证分析

2.1 主成分模型的建立与分析

以我国31个主要城市[4-6]作为研究主体，选取2017年数据中的X1～X6共6个指标数据进行研究.数据来自国家统计局官网2008年统计年鉴，相关数据见表1.

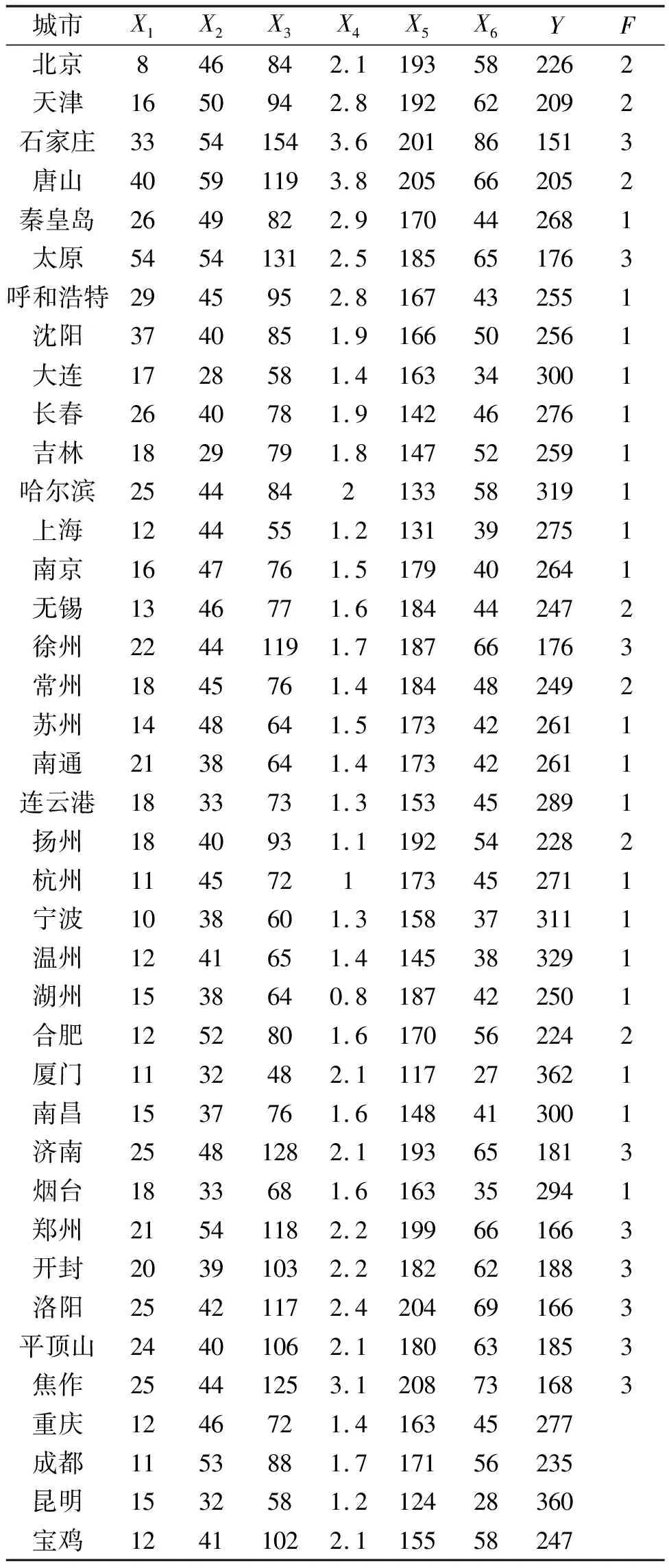
表1 各个城市的空气质量数据

数据中各个变量所代表的内容如下：

X1：二氧化硫年平均浓度(ug/m3);

X2：二氧化氮年平均浓度(ug/m3);

X3：可吸入颗粒物(PM10)年平均浓度(ug/m3);

X4：一氧化碳日均值第95百分位浓度(mg/m3);

X5：臭氧(O3)日最大8 h第90百分位浓度(mg/m3);

X6：细颗粒物(PM2.5)年平均浓度(ug/m3);

Y：空气质量达到及好于二级的天数(天);

F:类别(1：优,2：良,3：中).

注：1、2、3是根据Y对各个城市的分类.

由表2可知，KMO Bartlett检验变量是否适合因子分析,其值为0.800适合因子分析，Bartlett的值为179.180，p值为0.000<0.05，适合因子分析.

表2 KMO 和 Bartlett 的检验

由表3的相关矩阵可以看出，存在变量与变量之间的相关性，即认为各个变量之间存在一定的联系，由此可以从多个指标中提取几个主成分做主成分分析.

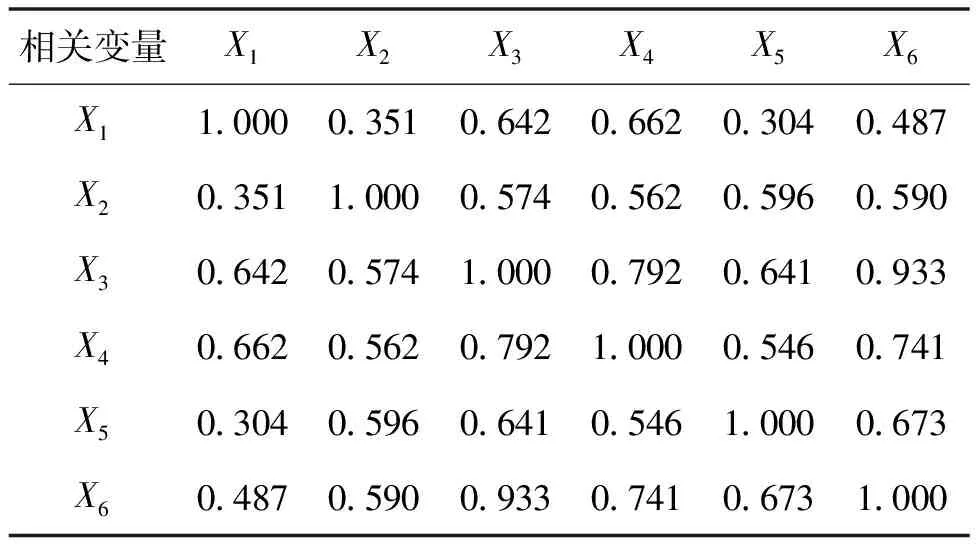
表3 相关矩阵表

由表4可知，公因子方差分析表中给出的主成分提取每个原始变量的信息,从表中可以看到主成分包含几乎80%的变量信息,信息提取充分.

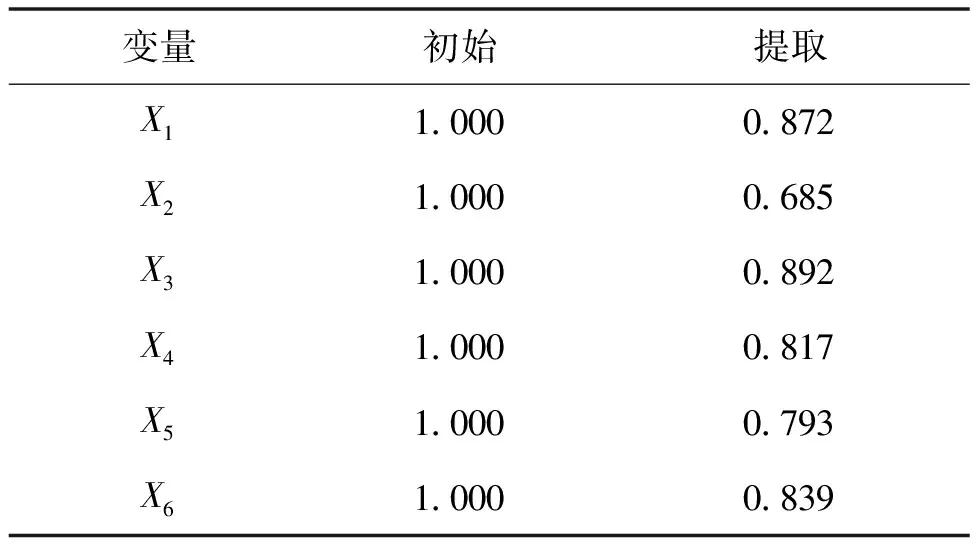
表4 公因子方差表

由表5可知，特征根和方差贡献率表给出了各主成分解释变量总方差所占百分比的情况，可以看到保留2个主成分,占总数的81.632%的信息,并且是80%以上.最大特征根是4.080、0.818.由图1还可以看到,保持两个主要组件可以总结大部分信息.因此,保留2个主成分比较合适.

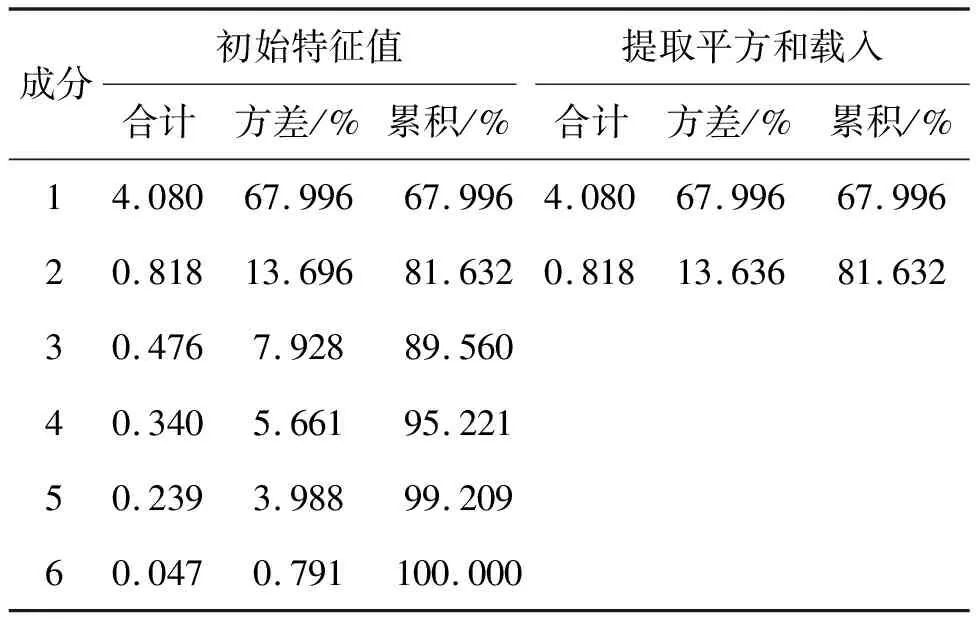
表5 特征根与方差贡献率表

由表6可知，第一主成分由X3、X4、X6确定，第二主成分由X1、X2、X5确定.

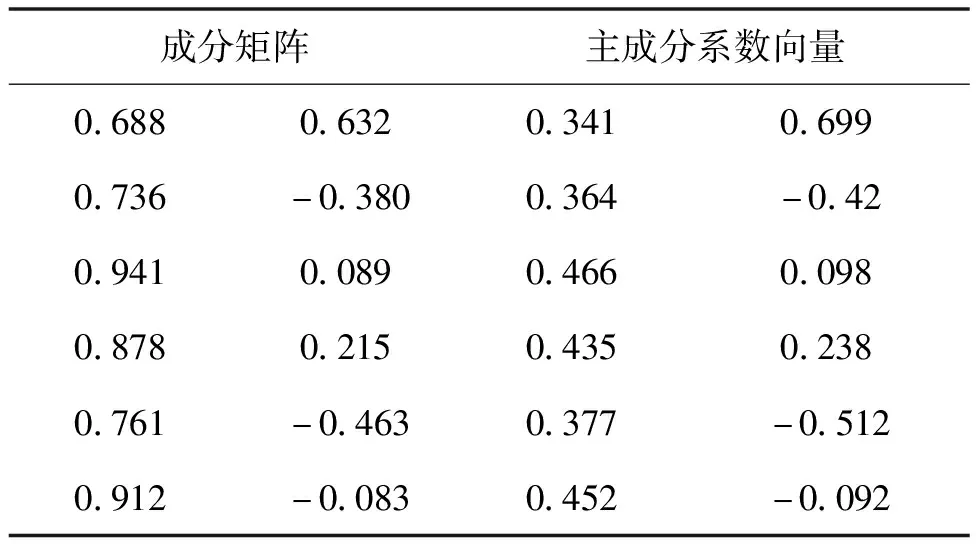
表6 成分矩阵及系数向量

根据主成分分析公式，建立主成分分析评价模型：

F1=0.341×X1+0.364×X2…+0.452×X6，F2=0.699×X1-0.42×X2…-0.092×X6，F综合=0.833×F1+0.162F2.

从累积贡献率还可以看到前两个主成分的累积贡献率为81.632%,基本上概括了环境空气质量污染的大部分信息.这表明,污染空气质量主要是煤炭、工业排放、粉尘和其他排放的烟尘、机动车尾气等,所以应增加检测和管理工作.

运用各个城市的指标和系数公式计算出城市的整体污染指数的得分排名，更加明了地判断各个城市的空气质量，对城市的空气质量控制和改善提供帮助.由主成分得分数据显示的结果可以看出：厦门、上海、昆明、沈阳等几个城市的综合得分最低，空气污染相对较轻，空气质量相对较好；石家庄、太原、唐山、焦作等几个城市的综合得分最高，空气污染较为严重，空气质量相对较差.空气质量的好坏与城市的经济发展、工业产区的多少、城市对空气污染的治理力度等多方面因素有关.各地区政府能更加了解城市的空气质量程度，加大治理力度，促进城市的发展.

2.2 主成分费希尔判别的建立与分析

根据主成分[7-11]的分析结果得出X3(可吸入颗粒物(PM10)年平均浓度)、X4(一氧化碳日均值第95百分位浓度)、X6(细颗粒物(PM2.5)年平均浓度)在空气污染指标中所占比重较大，是污染空气的重要来源.变量的系数见表7.

表7 典型判别式函数系数

根据费希尔相关公式，建立发展费希尔判别函数模型：

y1=-8.350+0.097X3-1.729X4+0.062X6，

y2=-1.763-0.119X3+0.985X4+0.200X6.

根据不同的判别函数对各个城市的指标进行分析，选用两个函数y1和y2,将各个城市的指标X3、X4、X5的值分别带入y1和y2函数中，构成坐标(y1,y2).由表8写出优、良、中3种类型的类中心位置：优(-1.683，-0.199)、良(0.075,0.816)、中(3.495，-0.215)，在excel中分别用两点间距离公式计算出(y1,y2)到(-1.683,-0.199)、(0.075,0.816)、(3.495,-0.215)三个类别中心点的距离，根据距离最小的原则，判别(y1,y2)所属的类别.

表8 组质心函数

1)误判率.数据中与三个类别误判:城市中吉林所属类别2误判给1；哈尔滨所属的类别2误判给1；无锡所属的类别1误判给2；误判率=6/39*100%=15.3%.

2)预测.重庆距离类别1的距离为1.203,最小，判重庆属于类别1；成都距离类别2的距离为0.298,最小，判成都属于类别2；昆明距离类别1的距离为2.789,最小，判昆明属于类别1；宝鸡距离类别3的距离为1.749,最小，判宝鸡属于类别2.

表9对未分类的城市的判别结果与费希尔公式计算的判别结果基本一致:第一类中有三个城市所属2类误判给1；第二类中有一个城市所属3类误判给2，一个城市所属1类误判给2；第三类中有一个城市所属2类误判给3.整体的误判率为6/39,误判率偏小，认为费希尔判别法可普遍用于城市的类别判断.

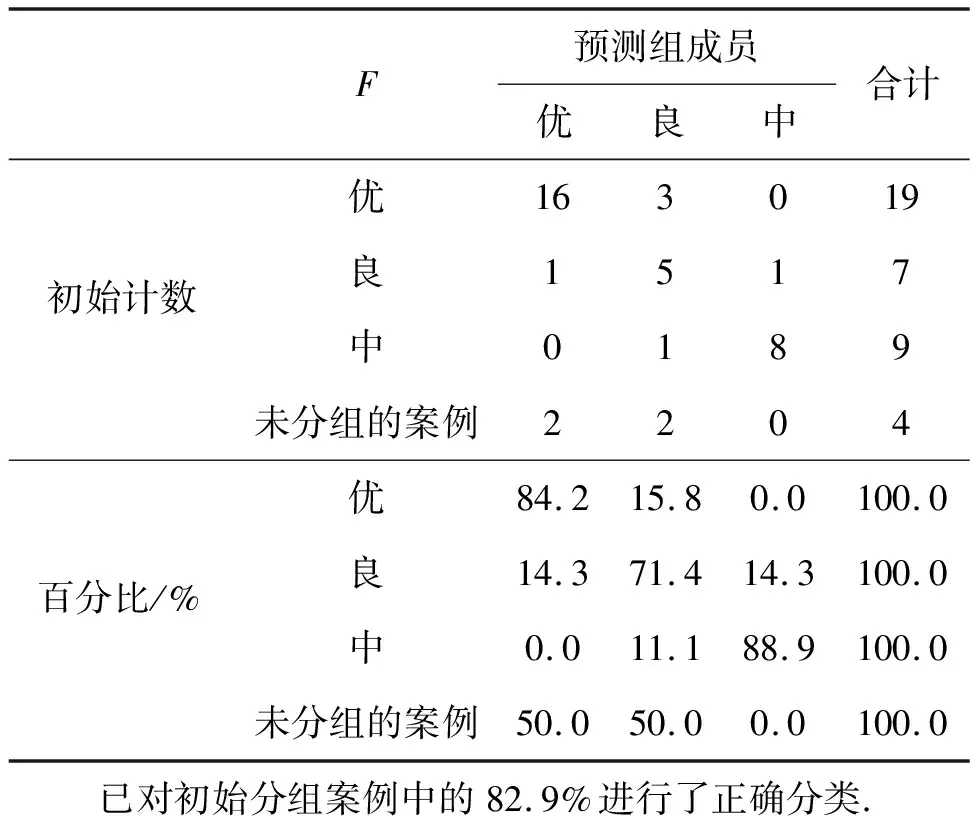
表9 分类结果

典则判别函数对各个城市的所属类别做了详细的描述，各类型的城市均在各个组质心周围分散分布(图2).对于待分组的城市所属类别做出了判别.

3 结 论

1)减少交通废气的污染：减少汽车废气污染，关键在于改善发动机的燃烧设计和提高汽油的燃烧质量，使燃油得到充分的燃烧，从而减少有害废气.

2)改变燃料构成：实行煤向燃气的转换，同时加紧研究和开辟其他新的能源，如太阳能、氢燃料、地热等.这样，能够大大减轻烟尘的污染.

3)绿化造林：茂密的林丛能降低风速，使空气中携带的大粒灰尘下降.树叶表面粗糙不平，有的有绒毛，有的能分泌黏液和油脂，因此能吸附很多飘尘.蒙尘的叶子经雨水冲洗后，能继续吸附飘尘.如此往复拦阻和吸附尘埃，能使空气得到净化.

4)宣传低碳生活：加大力度宣传节约资源，践行绿色生活.从一点一滴中做到对环境的保护.