基于广义Logistic模型的美国白蛾优化控制策略
张巧玲, 陆海霞*, 张 翼
(1. 宿迁学院文理学院, 江苏 宿迁 223800; 2. 沈阳工业大学理学院, 沈阳 110870)
1 预备知识
本文在描述美国白蛾种群密度时, 将模型dN/dt=rN(1-N/K)p中的调整系数p取为3.基于美国白蛾繁殖规律,考虑到对美国白蛾的捕获努力量, 则美国白蛾种群可描述为

(1)
其中x(t)为t时刻美国白蛾种群的密度.不失一般性, 所有参数均为正值.
2 主要结果
2.1 平衡点的存在性及稳定性
模型(1)所描述的美国白蛾种群密度增长速度如图1所示.从图1可以看出, 只有当美国白蛾负增长时, 外来物种对环境的影响才会减弱.当美国白蛾负增长时, 其种群密度已超过环境的最大容纳量K, 打破原有平衡, 故考虑捕获努力量E.设捕获函数h(x)正比于种群密度和捕获努力量的乘积, 即h(x)=qEx(t), 其中捕获能力系数q>0, 则美国白蛾种群密度可描述为
(2)
引理1若系统(2)中参数均为正常数, 且满足r>qE, 令x(t)为系统(2)的平衡点, 则对所有t≥0, 系统(2)的平衡点在[0,+∞)上.
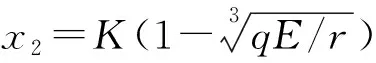
系统(2)的平衡点是直线y=h(x)与曲线y=f(x)的交点(见图2), 即方程rx(1-x/K)3-qEx=0.由于其导数为r(1-x/K)2(1-4x/K)-qE, 易证:
定理2x=0是系统(2)的平衡点,且当r>qE时, 系统不稳定.
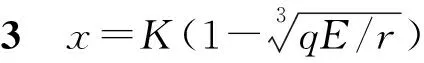
2.2 种群动力学性质
图2为不同情况下系统(2)的平衡点位置.图2(a)显示, 当y=h(x)与y=f(x)有唯一交点x=0时, 比较2条曲线在原点的斜率可知, 此时qE=r,说明当线性捕获系数达到其内禀增长率时, 美国白蛾的种群密度可控制为零.图2(b)显示, 此时y=h(x)与y=f(x)也是只有唯一交点x=0, 比较两条曲线在原点的斜率可知, 此时qE>r, 说明美国白蛾的入侵得到了有效控制, 防治和捕杀工作效果显著, 显然这个阶段的状态不会持续很久就会趋向于图2(a)的状态.图2(c)显示, 当y=h(x)与y=f(x)有正交点x*时, 由2条曲线在交点前的斜率可知, 美国白蛾种群密度的增长率先增后减, 得到了有效的抑制作用, 此时qE 定理4在D中使得H(E)取得最大值的最优捕获努力量E*=27r/(64q), 相应的最大捕获量H*(E*)=27Kr/256, 优化控制的美国白蛾密度x*(E*)=K/4. 本文基于广义Logistic模型, 研究了美国白蛾繁殖速度与捕获系统的动力学性质,分析了平衡点及其系统处于稳定状态的充分条件, 并给出了在正平衡点处可持续发展的最大捕获努力量E*=27r/(64q), 使美国白蛾的种群密度控制为最大容纳量的1/4.2.3 美国白蛾的优化控制
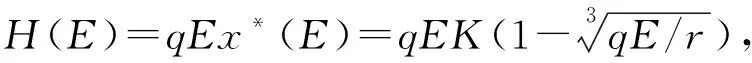
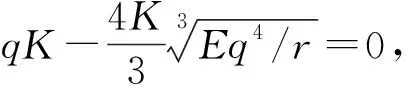
3 结论

