基于URANS的Ahmed模型外流场分析

吴华杰, 张善文, 张燕军*

(1. 扬州大学a. 汽车及其零部件数字化设计与制造技术工程中心; b. 机械工程学院, 江苏 扬州 225127; 2. 扬州工业职业技术学院机械与汽车工程学院, 江苏 扬州 225127)

符合空气动力学的汽车外型不仅更符合设计审美标准,而且能够降低汽车空气阻力、减小气动噪声, 提高汽车的整体性能．风洞试验是研究汽车空气动力学的重要方法之一, 但风洞试验具有试验周期长、投资大等缺点．而运用计算流体动力学(computational fluid dynamics, CFD)方法, 可以通过调节参数对不同汽车流场工况进行仿真计算, 不仅大大缩短了研发周期,而且可以直观地获取各个时刻、各个位置的相关物理量信息[1-3]．汽车外流场问题是一种典型的钝体绕流问题,汽车外表面能干扰来流,从而使下游流场呈现出丰富的流动状态, 流场结构具有三维效应和非定常性等特点,建立合理的数学模型对此类流场特征进行捕捉是汽车外流场仿真的主要难点之一, 国内外学者采用不同湍流模型对汽车外流场的仿真模拟开展了较深入的研究[4-7]．结果表明: 采用雷诺时均模拟方法(Reynolds averaged navier-stockes, RANS)很难对流场的典型流动特征进行捕捉[8], 而大涡模拟方法(large eddy simulation, LES)或LES与RANS相结合的方法虽然可以提高计算精度并捕捉到丰富的流动特征, 但计算时间较长,且对计算机硬件要求较高[9-10]．本文拟采用非稳态雷诺时均模拟方法(unsteady Reynolds averaged navier-stockes, URANS)对尾部倾角为25°的Ahmed模型[11-12]的外流场进行数值仿真研究, 并将预测的时均流场信息与试验数据进行对比, 分析1个典型周期内的非稳态流场, 为后续汽车外型优化设计提供一套合理可靠的模拟方法．

1 计算模型及数值方法

1.1 Ahmed模型

Ahmed模型的试验数据被广泛用于验证汽车外流场模拟程序的可靠性[13]．Ahmed模型的几何尺寸信息如图1所示, 其中φ为尾部倾角,本文采用的Ahmed模型其尾部倾角为25°[14]．

1.2 控制方程与湍流模型

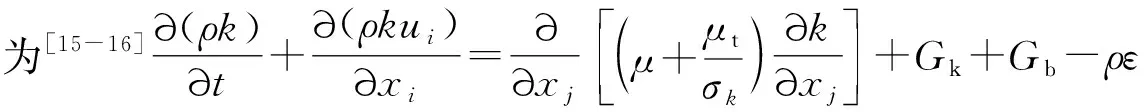
1.3 边界条件及求解设置

1.4 网格无关性分析

表1为3套网格的阻力系数计算结果与文献[8]中采用大涡模拟结果的对比．结果表明, Mesh 1与Mesh 2的计算结果有较大差异; 随着网格数量的增加,Mesh 3与Mesh 2的预测结果误差在5%以内, 故Mesh 2能给出网格无关性的模拟结果; 采用标准k-ε湍流模型进行瞬态计算的结果与采用大涡模拟的预测结果相近, 这表明基于URANS的标准k-ε湍流模型模拟方案能够给出可靠的仿真结果．

表1 网格无关性分析结果

2 结果与讨论

2.1 尾部区域时均流场分析

为便于与试验结果对比, 在计算域中分别离Ahmed模型的后表面0,80, 200, 500 mm处截取4个截面．图3为不同截面上速度矢量分布．从图3可以看出, 在x=0 mm的截面上u≥0, 表示该处没有出现回流现象, 但模拟结果显示位于尾部上方两侧存在流体旋涡; 在x=80 mm的截面上,u值出现了负值, 说明该处流体有回流, 且由上游发展而来的漩涡在此处仍然存在,其影响区域有扩大的趋势,模拟预测的速度分布与试验结果较为一致; 在x=200 mm的截面上,u的负值区域开始减小,两侧漩涡向靠近地面的方向发展, 使得该处出现丰富的流动现象, 此截面处模拟预测结果与试验测量结果吻合; 在x=500 mm的截面距离Ahmed模型尾部较远, 仿真结果表明此处回流区域基本消失, 两侧漩涡发展范围进一步扩大至地面区域, 而试验结果表明, 此处两侧漩涡中心的低速区域呈现凹型分布特征[11]．

为进一步研究Ahmed模型两侧漩涡的发展规律, 将模拟结果的时均速度场进行处理以获取涡量在x方向上的分布．图4为Ahmed模型在不同截面上时均涡量分量ωx的分布情况．从图4可以看出, 在Ahmed模型的平直段, 两侧涡量分量均为0 s-1, 表示此处没有产生漩涡;在Ahmed模型尾部倾斜段位置, 涡量ωx在两侧分别出现一正一负的区域, 表明2个漩涡的旋转方向相反; 在Ahmed模型尾部倾斜段的下游位置(见图4(c)), 两侧漩涡处的涡量分量正负值区域进一步扩大, 但漩涡强度并未减弱, 表明漩涡在不断发展．图4(d)显示, 在距离Ahmed模型尾部区域的截面上,两侧漩涡的影响区域继续扩大, 但漩涡强度明显降低．因此, Ahmed模型尾部的倾斜段是产生两侧漩涡的诱因,漩涡生成以后沿着尾部倾斜段不断发展,在脱离模型后漩涡影响区域不断扩大,但其强度逐渐减小．

图5为Ahmed模型对称表面的时均压力分布．图5显示, 在Ahmed模型首部区域,压力从最大值快速减小至负压极小值;在模型平直段,下表面压力逐渐单调回升,而上表面压力逐渐增大后,在尾部倾斜部分的影响下再次出现负压极值．上下表面压力曲线并不重合,下表面压力曲线与横坐标轴所围面积大于上表面压力曲线与横坐标轴所围面积, 表明Ahmed在空气动力的作用下受到升力作用．

2.2 瞬态流场发展规律分析

图7为不同时刻Ahmed对称面所在平面上的流线分布．不同时刻空气在流过上下表面时都呈现出二维特性,但在临近尾部区域的流动呈现出三维特性,流动结构复杂多变,漩涡在此处形成,并不断向下游输运．A时刻,尾部区域存在2个漩涡;发展到B时刻时,上部漩涡区域范围有所扩大,下部漩涡从Ahmed模型下表面脱落; 在C时刻,上部漩涡仍存在,而下部漩涡已经向下游输运; 在D时刻,尾部区域的下部漩涡向下游输运了一段距离,而此时在Ahmed模型下表面已经开始再次诱导产生新的下部漩涡．

图8为不同时刻涡量分量ωy在对称平面上的分布情况．图8显示, 在Ahmed模型尾部流场区域,存在2个正负值区域的涡量分量ωy,其中正值表示漩涡为顺时针旋转,负值表示漩涡为逆时针旋转．在不同时刻,上方正值涡量区域相对稳定,而下方负值涡量区域形态改变明显,且下部漩涡由流体脱离下表面时产生,并周期性地向下游输运．

图10为Q=6 000 s-1时的等值面分布．按照Q准则理论这些等值面可视为涡结构, 在4个不同时刻, 顶涡较稳定地附着在Ahmed模型平直段与倾斜段的交线位置,而底涡由模型底面诱导产生,并不断向下游输运．同时,两侧角涡的结构呈现圆锥型,由顶部较小的涡结构向下游不断扩大,这与试验结果一致[11-12]．

3 结论

本文基于URANS方法, 采用标准k-ε模型对尾部倾角为25°的Ahmed模型的外流场进行了仿真计算分析．结果表明:

1) 网格分布对模拟结果产生较大影响, 在对Ahmed模型外流场进行数值模拟时, 需要进行严格的网格无关性分析;

2) 本文采用的计算方案所预测的阻力系数与大涡模拟方法的计算结果一致, 且试验测量的速度场分布证实了本文模拟结果的可靠性;

3) Ahmed模型尾部的倾斜段是产生角涡的诱因,角涡生成以后沿着尾部倾斜段不断发展,在脱离模型后角涡影响区域不断扩大,而强度逐渐减小;

4) 在本文计算工况下, Ahmed模型外流场呈现周期性变化的瞬态特征, 采用Q准则为6 000 s-1时的等值面能够识别出流场中3个典型涡系．