整数带余数除法定理的再认识
夏咪咪, 陈 若
(湖州师范学院 理学院, 浙江 湖州 313000)
0 引 言
带余数除法定理不仅是初等数论的基础,而且在高等代数及近世代数中占有一席之地.带余数除法定理从整数环、多项式环、高斯整数环推广到一般的欧氏环,是这些环理论的基础.整数带余数除法是数论中整数整除理论的一个重要组成部分.
带余数除法定理的应用十分广泛,是小学到大学阶段数学学习的重要内容.带余数除法在小学低年级数学中就有涉及,并常常被概括为这样的形式:被除数÷除数=商……余数,如10÷4=2……2.初中数学也涉及多项式除法的学习,如根据等式2x3+9x2+9x+6=(x2+4x+1)(2x+1)+(3x+5),可知2x3+9x2+9x+6除以x2+4x+1的结果.高中及大学也会继续学习该内容并逐步加深.带余数除法定理是研究整数和多项式整除理论的一个基本方法,所以深入研究该理论十分必要.
本文对整数带余数除法定理进行系统的研究,介绍带余数除法定理及其历史发展,并用多种方法给出相关证明,从不同角度对带余数除法定理进行深入理解.同时举例说明带余数除法定理在数学教学及跨学科中的应用.该研究用带余除法定理的思想方法将小学到大学的相关知识串联起来,便于学生系统性地加深对知识的理解.
1 带余数除法定理与历史发展
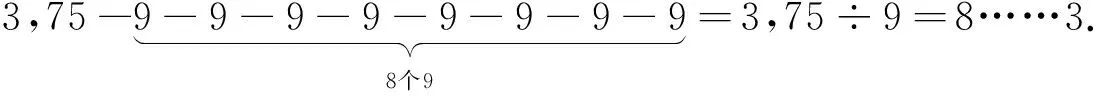
定理1[2]若a,b是两个整数,其中b>0,则存在两个整数q及r,使得
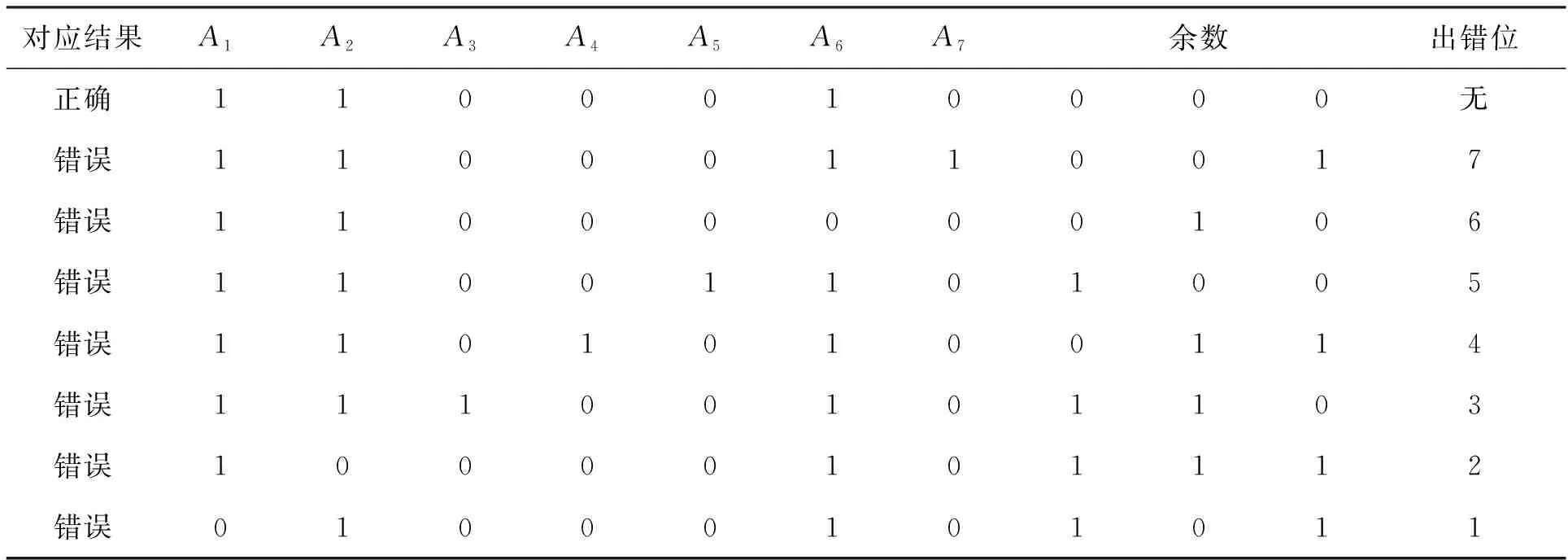
a=bq+r, 0≤r (1) 成立,且q及r是唯一的.我们把q称作a被b除所得的不完全商,r称作a被b除所得的余数.当r=0即a=bq时,我们就说b整除a,记作b|a. 该定理称作带余数除法定理,整数的一些基本性质可由此定理推导得出.在该定理中,假设a=173,b=21,则有a=8b+5,r=5<21,q=8,其中q、r是唯一的. 中国古代《九章算术》中介绍的“更相减损术”,实质上就是应用带数除法定理,原是为约分设计的,而后应用于任何求最大公约数的场合.书中记载到“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之”[3].所利用的原理就是gcd(a,b)=gcd(a-b,b).以77和56为例. 77-56=21, 56-21=35, 35-21=14, 21-14=7, 14-7=7, 可知gcd(77,56)=7.更相减损术是利用减法原理来求两数的最大公约数.在西方欧几里得创设了用除法原理求公约数的方法,即辗转相除法. 定义1对任意两个整数a,b>0,重复应用带余数除法,有: a=bq1+r1, 0 rn-1=rnqn+1+rn+1,rn+1=0. 由于余数是小于除数的非负整数,除数是正整数,所以重复进行带余数除法能得到一个余数是零的等式,这样的计算方法即为辗转相除法. 利用辗转相除法可求出两个正整数的最大公约数,如求1 537与1 749的最大公约数.因为1 749=1×1 537+212,1 537=7×212+53,212=4×53,所以(1 537,1 749)=53. 由辗转相除法可得到整数整除理论中几个重要定理的关系,如图1所示.这3个重要定理构成了整数整除理论的主要内容.因此,带余数除法定理可以说是整数整除理论的基石. 定理1有多种证明方法,本文系统梳理了几种证明方法,其中有的证法对中学数学的教和学都有一定帮助. 带余数除法定理的存在性可以通过实数与数轴关系进行证明.该证法通俗易懂,对中小学数学的学习有一定帮助,特别是可以帮助学生理解数轴的作用. 证明如图2,以b为长度单位建立数轴. 根据实数与数轴上点的一一对应关系,必然存在唯一整数q,使得a在区间[qb,(q+1)b)内,令a-qb=r,则a=bq+r,其中0≤r 证毕. 证明带余数除法定理存在性的一般方法是数学归纳法.该证法的思想一直贯穿中小学数学学习的整个过程. 证明易得a<0时与a>0时的证明过程类似,为简明不妨假设a≥0,则 (Ⅰ)若a (Ⅱ)若a≥b,对a用数学归纳法:假设对n ①若a' ②若a'≥b,则由归纳假设有a'=bq'+r,0≤r 证毕. 该方法主要利用自然数的最小数原理.最小数原理是自然数所具有的一种基本性质,即任何非空的自然数集中都有最小的自然数.这一原理是数学归纳法的基础. 证明 (Ⅰ)若b|a,即a=bq,q∈Ζ,取r=0时等式(1)成立; (Ⅱ)若b⫮a,则有r≠b.设集合A={a+kb,k∈Ζ}在k=k0时,取得最小正整数r=a+k0b,则必有0 若r>b,即a+k0b>b,a+(k0-1)b>0,这与最小正整数r的取值矛盾,故0 证毕. 高斯函数在中小学解题时常出现,学生对其并不陌生.利用高斯函数对带余数除法定理进行证明,有助于加强学生对教材外所学知识的理解和应用. 设x∈,记[x]为不超过x的最大整数,{x}=x-[x].称[x]为x的整数部分,{x}为x的小数部分,并把y=[x]称为高斯函数,如 证明假设在数1,2,…,a(a>0)中能被b整除的整数有k个,由于能被b整除的正整数是b,2b,3b,…,故 证毕. 除了上述4种方法可以证明带余数除法定理的存在性外,还可以通过C语言编写实现整数带余数除法的函数,完成对该定理的机器验证[4]. class INT { public: INT(int a) { x=a; } int x; }; 再定义运算符的重载: int operator/(INT x,int y) { return quo(x.x,y); } int operator/(int x,INT y) { return quo(x,y.x); } int operator/(INT x,INT y) { return quo(x.x,y.x); } int operator % (INT x,int y) { return rem(x.x,y); } int operator % (int x,INT y) { return rem(x,y.x); } int operator % (INT x,INT y) { return rem(x.x,y.x); } 给出进行调用的主函数: void main( ) { int x, y; cout<<"x="; cin>>x; cout<<"y="; cin>>y; cout<<"x/y="< cout<<"x%y="< } 带余数除法定理是初等数学的重要组成部分,在现实生活中应用广泛.因此在中小学的数学学习中备受关注,此外,在不同学科中的应用也很广泛.早在公元5世纪,我国的《孙子算经》中就出现了一元线性同余方程组问题,其解法被称为孙子定理,又叫中国剩余定理.孙子定理的实际应用十分广泛,如计算机软件技术、编写与密码、数字通讯等领域.孙子定理的重要性不言而喻,其理论依据就是带余数除法定理.下面通过典型例子列举带余数除法在整除、不定方程、单位根及跨学科4个方面的应用. 分析注意到相邻两个整数中总有一个是偶数,所以对任意整数n,n(n+1)能被2整除,于是只要证明对任意整数n,n(n+1)(2n+1)能被3整除即可.将全体整数除以3,按余数可分为3类:{0}、{1}和{2},只要证明整数n取{0}、{1}和{2}中的任何一个数,n(n+1)(2n+1)都能被3整除即可. 证明对任意整数n,n(n+1)是偶数,所以n(n+1)(2n+1)能被2整除. 对任意的整数k,当n=3k时, n(n+1)(2n+1)=9k(k+1)(6k+1); 当n=3k+1时, n(n+1)(2n+1)=3(2k+1)(3k+1)(3k+2); 当n=3k+2时, n(n+1)(2n+1)=3(k+1)(3k+2)(6k+5). 证毕. 例证明:若n=9k+t,t=3,4,5或6,k∈Ζ,则方程x3+y3=n没有整数解. 分析不定方程不仅内容十分丰富,而且许多不定方程的解法有其特殊性.下面简要介绍一种最具普遍性的方法——余数分析法.余数分析法是利用带余数除法定理将不定方程的解按某个正整数的余数分类,考察方程中的项对某个正整数的余数. 证明对任意的整数x,y,记 x=3q1+r1,y=3q2+r2, 0≤r1,r2≤2,q1,q2∈Ζ, 则 其中, R1=0,1或8,R2=0,1或8,R=0,1,2,7或8. 由此得到所要证明的结论. 证毕. 带余数除法定理在不定方程中应用广泛,而且不定方程在实际生活中具有重要意义.这其中也渗透了建模思想,即将实际问题转化成数学模型,再运用数学模型更好地解决生活中的问题.数学建模是数学世界与实际生活之间的桥梁,通过建模有利于培养学生的抽象思维能力,以及提出问题、分析问题和解决问题的能力. 例正整数n的全体正因数di(i=1,2,…,n),则所有di(i=1,2,…,n)次原根就是全体n次单位根. 证明设ε是任意di次原根,则εdi=1.又因为di|n,设n=dimi,则εn=(εdi)mi=1,即ε是一个n次单位根. 反之,设εn=1且d是使εd=1的最小正整数.令 n=dq+r, 0≤r 则εr=εn-dq=1.由d的最小性知,r=0.故d|n,即d是d1,d2,…,dt中的一个. 设d=di(1≤i≤t),并由d的最小性(即ε是一个不低于di次单位根)知,ε是一个di次原根. 证毕. 单位根有很多性质,在解方程、循环行列式、循环矩阵中都有重要应用.其中也蕴含了丰富的思想方法,单位根的学习可以开拓学生的数学视野,拓宽学生的解题思路. 在网络信息传递的过程中,由于传输系统是人为设计的,难免会出现差错,导致信息接收者收到错误的数据信息.为提高准确率,需要在数据中增加校验码.校验码通常位于一组数字的最后一位或多位,由前面的数字经某种运算后得出,用以检验该组数字的正确性.介绍CRC(循环冗余)校验码,其作用是检验数据的正确性并对错误数据进行纠正. CRC运算的数学本质是带余数除法定理,其编码的过程是先约定一个“生成多项式”,再用一个新定义的多项式对“生成多项式”作模二除法得到校验码,将该校验码放在源数据码之后形成CRC码进行传输.若接收到的CRC码能被“生成多项式”整除,则说明传递无误,否则需要通过校验位查出出错的位置并进行还原. 例位数为n的校验码共有2n种情况,如位数为3的校验码有000、001、010、100、011、110、111、101这8种,除了正确的1种外还存在7种错误可能.现在有生成多项式G(x)=x3+x+1和二进制序列为1 100的源数据码,若数据接收者得到的CRC码为1100110,问CRC码是否存在出错位(假设仅存在单个错)? 解检验得到的CRC码需要对生成多项式G(x)作模二除法,若余数为0则传递无误,否则有误,且不同位数出错余数不同,具体见表1. 表1 余数与出错位对应关系表 由于CRC码对生成多项式G(x)作模二除法后得到的余数是100,因此可知该CRC码存在错误,出错位为第5位. 解毕. 不同位数的CRC码都有类似的计算方法,其核心都是带余数除法定理.例4的求解是对二进制进行模二除法得到余数,也可以将二进制转化为十进制进行除法,再将得到的余数转化为二进制,其运算本质相同. 此外,带余数除法还在光通信系统[6]、单循环比赛安排[7]等方面有着重要的作用. 本文对带余数除法的历史、证法、应用等方面进行了再认识.根据带余数除法的证明和列举的应用发现,带余数除法的研究是非常有意义的数学研究之一,具有较高的实用价值,值得继续探究.
rn-2=rn-1qn+rn, 0
2 带余数除法定理的存在性证明
2.1 带余数除法定理与数轴

2.2 带余数除法定理与数学归纳法
2.3 带余数除法定理与自然数最小数原理
2.4 带余数除法定理与高斯函数

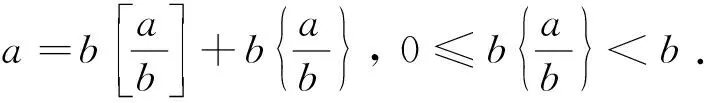
2.5 带余数除法定理与计算机程序
3 带余数除法定理的应用
3.1 在整除中的应用

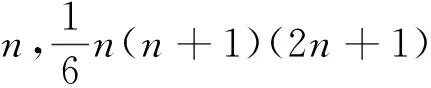
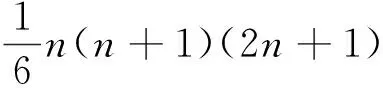

3.2 在不定方程中的应用
3.3 在单位根中的应用
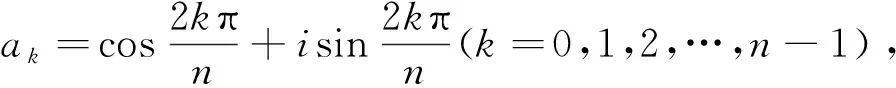
3.4 在信息传递中的跨学科应用
4 结 语

