改进PSO优化核SVR的锂离子电池剩余寿命估计

宋 涛， 甄爱钢， 徐静云,,3， 李自恒， 孟文斌

(1.湖州师范学院 工学院， 浙江 湖州 313000；2.浙江天能新材料有限公司， 浙江 湖州 313100；3.湖州市新能源技术研究所， 浙江 湖州 313100；4.浙江工业大学 信息工程学院， 浙江 杭州 310014)

0 引 言

锂离子电池(简称锂电池)具有能量密度高、循环寿命长等优点，被广泛用于新能源汽车、3C消费和通信基站等领域.但锂电池经反复充放电后，电池内部会产生正负电极材料活性下降、电解液损耗和隔膜老化等问题，从而引起电池容量下降，剩余寿命(remaining useful life，RUL)缩短，对用电设备/系统带来安全性和可靠性问题.对锂电池RUL进行估计，有助于用户及时维护或更换电池，提高用电设备/系统的安全性和可靠性[1].

传统的锂电池RUL估计方法主要包括基于经验的方法和基于性能的方法两类.基于经验的方法是根据经验知识来判定电池是否失效，其估计结果较粗糙且普适性差.基于性能的方法包括基于模型的方法和基于数据的方法两类.基于模型的方法是根据电池电极材料、电解液和隔膜老化机理构建退化模型来预测RUL.由于目前锂电池内部的退化机理尚不明确，因此极难建立简单准确的退化模型.基于数据的方法是根据锂电池的历史数据来建立电池退化趋势曲线，从而预测电池至失效的循环次数[2].由于锂电池的历史数据较易采集，因此该方法已成为目前的研究重点.该方向的主流方法有人工神经网络[3]、自回归模型[4]、相关向量机[5]和支持向量回归[6]等方法.其中支持向量回归(support vector regression，SVR)是通过构建最小结构风险来获得最佳的拟合线性曲线的，以避免过拟合和欠拟合，且支持向量所需要的样本数极小，因此SVR对小样本数据集有优异的预测性能.文献[6]、[7]以充放电循环次数作为输入，以阻抗和容量作为输出，通过构建SVR模型来预测电池RUL.但锂电池容量的退化不是理想的线性关系.文献[8]引入核函数，通过构建基于核SVR模型来预测RUL，预测精度有了明显改善.但是惩罚因子C和核参数g的取值对预测性能有重大影响.为获得适用于具体电池组的最优C和g，引入PSO方法对参数进行寻优是个不错的思路.但基础是PSO方法存在易早熟收敛和收敛速度慢的不足[9-12].本文在对传统的PSO方法优化[11]的基础上，设计一种PSO优化方法(improved PSO,IPSO)，并与KSVR相结合估计锂离子电池RUL.该方法首先构建以充放电循环次数为输入，以电池容量为输出的核SVR模型，然后用IPSO算法优化惩罚因子C和核方差g，最后在筛选的NASA数据集上进行训练与测试，并以实验结果表明算法的有效性.

1 KSVR原理

给定的锂离子电池历史数据训练样本集：

(k,yk),k=1,2,…,M，

其中：k为充放电循环次数；yk为第k次释放出的电池容量；M为训练样本集数目.将k映射到高维空间φ(k)，建立非线性回归方程：

f(k)=ωTφ(k)+b，

(1)

其中：φ(k)为特征空间；ω和b分别为权重和偏置参数.根据结构风险最小原则，ω和b的参数值可以通过求解下列优化问题计算得到：

(2)

(3)

对上述目标函数各参数求偏导，化简后可转化成凸二次规划问题：

(4)

由此可推得非线性拟合函数为：

(5)

核函数K(j,k)=φ(j)Tφ(k)，其中j为训练样本输入量；k为测试样本输入量.对不同的应用问题，核函数的选择对SVR模型的拟合性能有明显差异.目前的核函数有10余种，主流有3种，即多项式核函数、高斯核函数和Sigmoid核函数，其中高斯核函数适用于锂离子电池容量估计场景[6].

2 IPSO优化方法

粒子群算法是通过群体中个体之间的信息交互来实现最优解求解的.该方法因简单易实现、参数少且能较快地找到全局或局部的最优解而被广泛用于参数寻找.线性权重衰减粒子群优化(linear decay inertial weight particle swarm optimization，LDWPSO)算法[10]、收缩因子粒子群优化(constriction factor particle swarm optimization，CFPSO)算法[11]均通过动态改变权重参数来改善PSO寻优能力.文献[12]通过引入指数衰减因子对权重进行优化，较快且容易找到全局最优解.本文在该方法的基础上设计一种IPSO方法，具体的算法原理如下：

针对KSVR的两个参数C和g，设计IPSO算法.设在2维搜索空间中存在N个粒子，第i个粒子的当前位置Xi=(Ci,gi)，当前速度Vi=(vi1,vi2)，在每次迭代过程中，个体所经历的最佳位置PPi=(Cpi,gpi)，群体所经历的最佳位置为PGi=(Cgi,ggi).则第i个粒子第t次迭代的速度更新公式为：

(6)

第i个粒子的位置更新公式为：

(7)

其中：下标i=1,2,…,N；θ为惯性权重；c1、c2为学习因子；r1、r2为区间在(0,1)之间的随机数.考虑到算法在前期的步长要大，后期的步长要小，以及迭代过程中对个体学习因子递减，对社会学习因子递增，有利于改善性能，本文对式(6)的惯性权重和学习因子设置如下：

(8)

其中：tmax为最大迭代次数；aE为指数衰减因子.

3 IPSO-KSVR算法

根据IPSO-KSVR算法原理，本文设计的算法步骤如下：

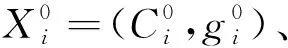
(2) 计算各粒子的适应度值.本文的适应度函数设计如下：

(9)

(10)

式中：yi为第i个循环次数电池容量实际值；Hbest为本次迭代的群体最大适应度值.

(3) 初始化粒子群个体和群体最佳位置PP和PG.

(4) 根据式(6)、式(7)和式(9)，更新各粒子的速度值、位置值，以及适应度、个体最佳位置、群体最佳位置.

(5) 判断是否达到最大迭代次数tmax，若达到则结束迭代，并将最佳位置值即参数(Cbest,gbest)输出，否则返回步骤(4).

(6) 将获得的最佳参数(Cbest,gbest)代入式(4)，得到非线性拟合函数所需参数值后进行预测.

4 实验与分析

本文选取美国航空航天局卓越故障预测中心电池组典型样本集B006.这组样本集电池为18650型钴酸锂电池，额定容量为2 Ah，测试环境温度为24 ℃，采用标准模式进行充放电.为便于数据分析，所有的样本集在处理前均进行归一化处理：

(11)

其中：Qi为第i次循环周期容量；Q0为电池初始容量.

为验证所设计的算法的有效性，本文选择网格法、LDPSO优化、CFPSO优化和本文所设计的IPSO优化方法，采用MSE、均方根误差(root mean square error，RMSE)、平均绝对误差(mean absolute error，MAE)、平均绝对百分比误差(mean absolute percentage error，MAPE)和相关系数R2来评价算法性能[13]，并通过百分比误差比较两种方法的性能改善程度.百分比误差定义为：

(12)

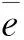
由图1和表1可见：

(1) IPSO-KSVR拟合结果与真实曲线最为接近；网格方法预测与实际容量包络偏差最大；LDPSO-KSVR和CFPSO-KSVR偏差介于网络方法和IPSO-KSVR方法之间.

(2) IPSO-KSVR方法的R2指标达99.6%，比CFPSO-KSVR、LDPSO-KSVR和网络方法分别提高0.01、0.04和0.05.本文提出的IPSO-KSVR方法比网格法，以及LDPSO-KSVR、CFPSO-KSVR方法的MSE百分比误差依次减少66%、37%和25%，RMSE百分比误差依次减少42%、24%和14%，MAE百分比误差依次减少58%、35%和33%，MAPE百分比误差依次减少63%、42%和41%，RUL百分比误差依次减少64%、53%和43%，预测精度符合工程需求.

总体看，本文提出的方法增强了PSO的全局搜索能力，避免掉入局部最优点.RUL估计性能优于传统方法.

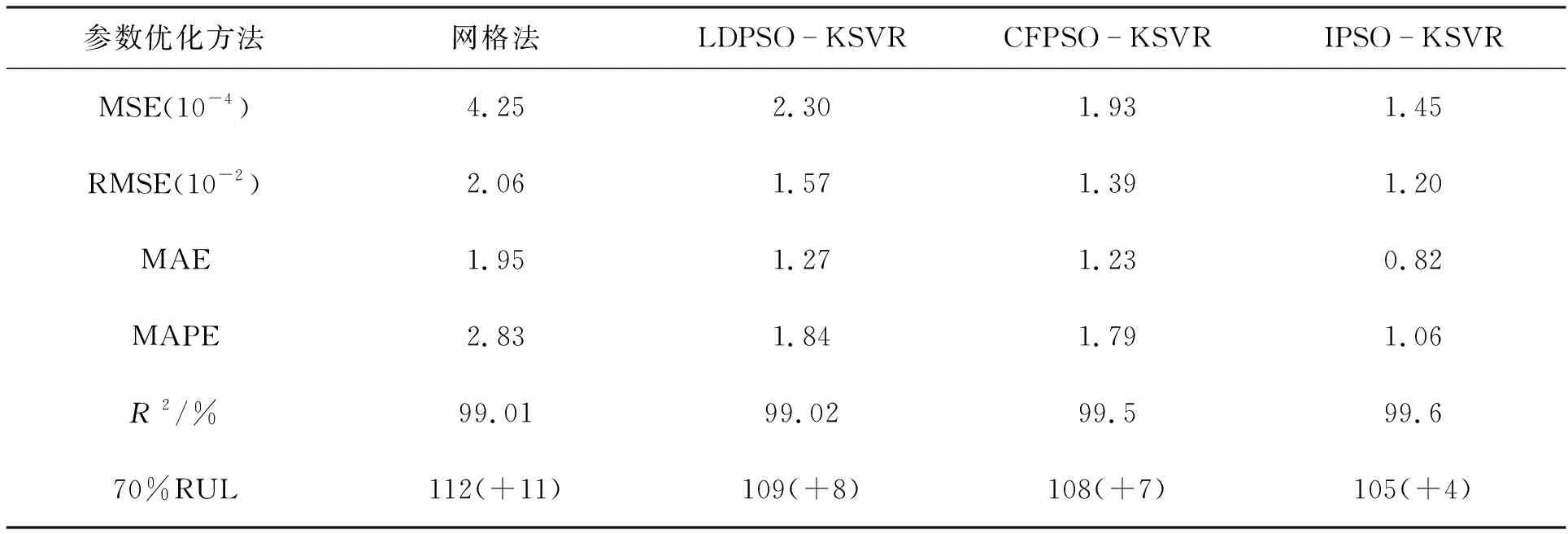
表1 4种KSVR算法的电池RUL预测性能评价(B006电池)

5 结 论

锂电池内部退化机理尚不明确，极难建立简单准确的退化模型.锂离子电池的历史数据中含有丰富的退化信息.传统的KSVR算法解决小样本、非线性估计问题具有独特的优势，通过较少的历史电池容量样本来估计RUL是一种典型的非线性拟合方法.本文提出一种IPSO-KSVR的锂离子电池RUL估计方法.实验结果表明，该方法与传统的KSVR方法相比，其电池容量估计MSE、RMSE、MAE和MAPE指标的百分比误差分别减少66%、42%，58%和63%，RUL预测百分比误差减少64%，优于其他PSO优化的KSVR方法.改进PSO优化核SVR的锂离子电池剩余寿命估计方法具有重要的理论与应用价值.