螺旋马丢高斯光束的非傍轴传输研究

曾胜财， 任志君， 简荣华

(1.厦门海洋职业技术学院 信息技术系， 福建 厦门 361100；2.浙江师范大学 浙江省光信息检测与显示技术研究重点实验室， 浙江 金华 321004；3.湖州师范学院 理学院， 浙江 湖州 313000)

无衍射光束最大的特点是光强分布沿传输方向始终不变.目前有4类无衍射光束，分别是椭圆坐标系下的Mathieu光束、极坐标系下的Bessel光束、直角坐标系下的Cosine光束和抛物坐标系下的Parabolic(抛物)光束[1-3].无衍射光束的研究在光学微操纵、制作光子弹、光通信等领域有着重要的应用.目前应用最广泛、技术最成熟的无衍射光束是贝塞尔光束.它是一种中心对称、光学形态相对简单的光束.无论是零阶贝塞尔光束还是高阶贝塞尔光束，其传输方程均可用较简单的数学函数来表达[4-5].因此贝塞尔光束是最容易实现，并被广泛应用的无衍射光束.

相比贝塞尔光束，马丢光束具有更多的形态[6-8]，表达形式也更复杂,在一些无衍射光束的应用领域中能达到特定的效果，因此对马丢光束的研究具有重要意义.目前国内外一些学者已经在马丢光束的表达形式、参数取值、传播属性，以及实验制作马丢高斯光束等方面进行了研究[6-12]，但大多是针对低阶马丢光束在傍轴的传输研究.吴琼等[13-14]提出用格林函数法和虚源法研究马丢光束，并给出了马丢光束传输更精确的表达式.但这些研究都是针对一阶奇次马丢光束，目前国内外尚未见关于更高阶马丢光束的研究，其主要原因是更高阶马丢光束的表达形式更复杂，无论是采用计算模拟还是光学方法，实现的难度都非常大，而马丢光束在非傍轴情况下传输的研究更复杂.本文利用虚源法，结合傅里叶-贝塞尔变换理论，以螺旋马丢高斯光束为例，计算模拟复杂马丢光束的传输表达式及非傍轴情况的光场分布，并与傍轴近似结果做对比分析，这对研究螺旋马丢高斯光束的传输特性及其应用具有一定的理论意义.

1 虚源法计算螺旋马丢光束

马丢光束经级数展开，在极坐标系下有4种光强表达形式[9]，分别是第一类、第二类奇型马丢光束和第一类、第二类偶型马丢光束.

(1)

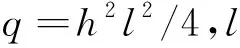
对应类型的奇、偶光束叠加可形成螺旋马丢光束.而理想的马丢光束仅是个理论模型，需要被高斯函数剪切，使其在有限范围内保持无衍射传输，才具有实际的研究意义.因此选择第一类奇型马丢光束和第一类偶型马丢光束的叠加为例，螺旋马丢高斯光束可表达为：

(2)

其在z=0平面的场分布为:

(3)

其中：ω0为z=0平面上光束的束腰宽度；2e+2为奇型马丢光束的阶数；2e为偶型马丢光束的阶数.利用虚源法将马丢函数展开.设有一系列强度为Scs(n)，n=2e+2j,位于z=zcs，半径ρ=ρcs，并带有一个方位角变量sin[(2j+2)φ]或cos2jφ的电环，只要参量Scs、zcs和ρcs选取合适的值，就能分别产生第一类奇型或偶型马丢光束.虚光源的标量波函数为：

E2e+2，2j+2(ρ，φ，z)=U2e+2,2j+2(ρ,z)sin[(2j+2)φ],
E2e，2j(ρ，φ，z)=U2e,2j(ρ,z)cos(2jφ).

(4)

近傍轴条件下，U2e+2，2j+2(ρ，φ，z)、U2e，2j(ρ，φ，z)均满足非奇次亥姆霍兹方程：

(5)

其中：k是波数；对于第一类奇型马丢光束和第一类偶型马丢光束，(m,n)分别取(2e+2，j+2)、(2e，2j).用傅里叶-贝塞尔在极坐标系下的变换可得[10]：

(6)

(7)

由式(5)可得关于Um,n(ρ,z)的光谱Fm,n(η,z)的微分方程.将Fm,n(η,z)代入式(6)，有：

(8)

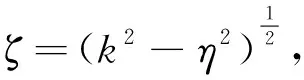
(9)

(10)

(11)

(12)

将式(10)～(12)代入式(9)，可得傍轴条件下Um,n(ρ,z)的近似解为：

(13)

将式(10)～(12)代入式(8)，可得Um,n(ρ,z)精确解的积分表达式为：

(14)

2 螺旋马丢光束的轴上光场分布

对第一类螺旋马丢高斯光束轴上ρ=0光场的非傍轴修正项，根据式(2)、式(4)和式(14)，可得轴上光场的分布为：

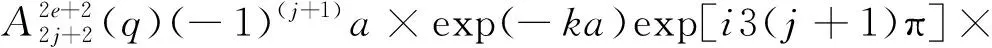
(15)

式(15)中的振幅因子1/ζ和相位因子exp[iζ(z-ia)]进行级数展开后，因η2≪k2，所以只需保留(kω0)-2e(e=0,1,2,…)及之前的项.为获取轴上光场的三阶非傍轴修正，有e=3，保留至(kω0)-6项即可.在此条件下的展开结果为：

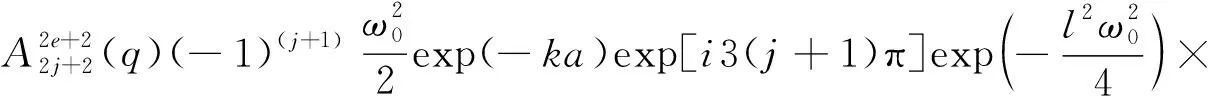
(16)

式(16)中:

(17)

式(17)中：f2(z)=(1+iz/a)-1，根据关系式

(18)

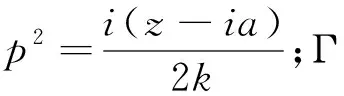
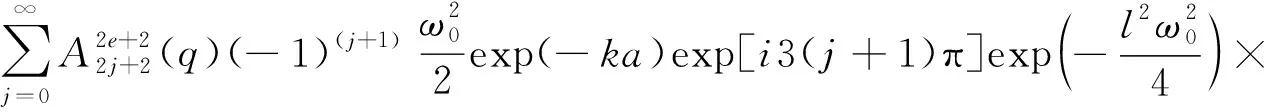
(19)

式(19)中：

(19)式为轴上的螺旋马丢高斯光束保留到三阶非傍轴修正项的非傍轴表达式.取λ=632.8 nm、ω0=45 μm、q=6，对螺旋马丢高斯光束的轴上非傍轴光强分布进行数值模拟，如图1所示(纵坐标光强的单位由初始光强而定).

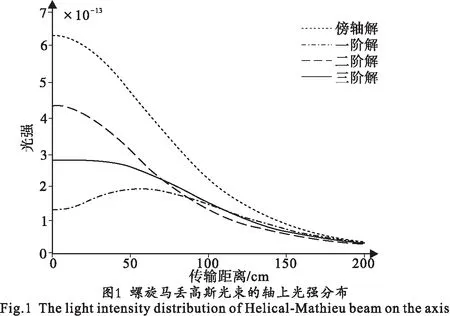
由图1可知，螺旋马丢高斯光束在传输过程中的近距离范围内，非傍轴修正值与傍轴近似值相差较大，随着传输距离的增加，两者越来越接近.因此，若将螺旋马丢高斯光束应用于近场研究，如光学加工或显微成像，需精确计算其非傍轴传输特性.但非旁轴理论的数学计算极复杂,一般很难给出解析表达式.本文基于虚源法计算推导螺旋马丢高斯光束的解析表达式,给出了非傍轴传输的精确解，此表达式能同时适用于近场和远场的光束传输情况，对解析研究复杂光束的传输具有极其重要的理论价值.

3 结 论

根据光束传输的独立性和叠加性原理，将螺旋马丢高斯光束分解成一系列Bessel光束叠加的形式，然后使用无穷项虚源求和的方法推导出螺旋马丢高斯光束在自由空间传输的严格解析积分表达式，并进行数值计算模拟其在光轴上光场分布的精确解，得到了螺旋马丢高斯光束保留到三阶非旁轴的修正项.此研究有利于了解螺旋马丢高斯光束的特性，在近场情况下，非傍轴修正值与傍轴近似值相差较大时，此光场精确解为螺旋马丢高斯光束在实际中的精准应用提供了有益的帮助.本文利用光束传输的特性，通过简单的函数叠加来实现对复杂光束的研究，此方法在光束传输和光场调制等方面有一定的意义.