2维Airy光束阵列强度的调控技术研究
张俊杰,安 岩,2* ,董科研,2,高 亮,2,李 响,2,张紫浩,陈亚楠
(1.长春理工大学 光电工程学院,长春 130022,中国;2.长春理工大学 空间光电技术研究所,长春 130022,中国;3.电磁空间安全国家重点实验室,天津 300308,中国)
0 引 言
随着有限能量Airy光束的生成,因其具有无衍射性、自加速性、自愈性的特点[1-3],引起了研究人员的广泛兴趣。近年来,在Airy光束的传输轨迹、光束强度、无衍射传输距离、光束特性、光束生成方法等方面[4-11]有了进一步的研究成果,其中具有自聚焦特性Airy光束的实验实现[12-13]推进了Airy光束在强度方面的研究。自聚焦Airy光束在传播过程中强度几乎保持不变,但在接近焦点(Airy光束自聚焦强度最大的位置)时峰值强度可突然增加几个数量级。Airy光束阵列[14]是自聚焦光束的一类,同样具有强度突增的特性,合成方式简单高效,对其强度方面的研究也是科研人员研究的重点方向。
2010年,HU等人[15]通过仿真和实验证明高斯光束在频域的位移,可以实现对2-D Airy光束峰值强度位置的调控,但对Airy光束阵列强度的调控需要进一步研究。2013年,ZHANG等人[14]在实验上实现了1-D Airy光束阵列合成自聚焦光束,实现了光束强度在焦点的扩展。2014年,CHEN等人[16]研究发现横向尺度因子可以控制Airy光束阵列自聚焦位置处强度的大小。2016年,EZ-ZARIY等人[17]推导了高斯光束阵列,生成了Airy光束阵列的表达式,并仿真实现了高斯光束阵列到Airy光束阵列的转换。2018年,WU等人[18]通过控制横向尺度因子实现了2-D Airy光束阵列自聚焦位置的移动。2019年,DAFNE等人[19]通过仿真和实验证明:施加线性和二次扰动因子,可以对Airy光束阵列能量分布实现控制。2022年,XU等人[20]通过对衰减因子、缩放因子的研究,实现了对自聚焦Airy光束强度、聚焦位置等的控制。以上研究表明,通过对光束或相位图不同参数的控制,实现Airy光束阵列强度的控制,在仿真或实验过程中,需要通过软件实时编码控制光束参数或相位图参数、在液晶空间光调制器上实时更换相位图,过程复杂,并且对于一定焦点处Airy光束阵列强度的增强还需要进一步的研究。
本文作者研究了高斯光束在频域上的移动对2-D Airy光束阵列焦点处强度的控制。首先介绍了Airy光束阵列的研究背景、意义;然后理论分析了高斯光束对2-D Airy光束阵列焦点处强度调控的原理;最后分别对2-D Airy光束峰值强度位置的调控、光束阵列的初始光强以及自聚焦过程、2-D Airy光束阵列焦点处强度的增强进行了数值仿真和讨论。该光束阵列调控方法操作简单,在激光光束能量的扩展,以及激光通信信号的稳定、激光医疗等方面具有一定的研究价值。
1 理论分析
2-D Airy光束阵列如图1所示。由4个单独的2-D Airy光束组成,其中间隔距离2c[21]表示2-D Airy光束阵列的光束间距。
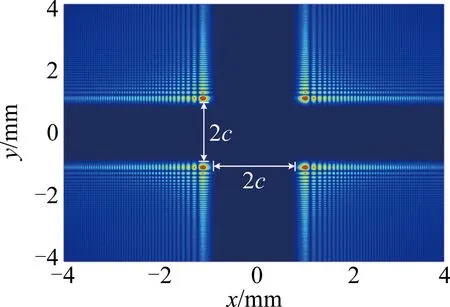
图1 2-D Airy光束阵列示意图Fig.1 Schematic diagram of 2-D Airy beam array
以点(c,c)为中心的2-D Airy光束的有限能量函数方程为[1]:
φ(sx,sy,ξ)=φ(sx,ξ)×φ(sy,ξ)=


(1)
式中:φ()为电场包络;A[·]为Airy函数;sx=(x+c)/x0和sy=(y+c)/y0为无量纲的横向坐标;x0和y0为横向尺度因子;ξ=z/(kx02)为归一化的传输距离,k=2π/λ为波束,λ为真空中波长;α为衰减因子,且0<α<<1。
因此,根据式(1),基于旋转矩阵理论[22]生成2-D Airy光束阵列,其函数方程为:
Φ(sx,sy,ξ)=φ(sx,sy,ξ)+φ(sx,-sy,ξ)+
φ(-sx,sy,ξ)+φ(-sx,-sy,ξ)
(2)
通过高斯光束在频域的位移原理,实现2-D Airy光束阵列焦点处强度的调控。为了便于理解高斯光束位移的理论,首先考虑1-D Airy光束生成高斯光束的位移,根据式(1)对于1-D有限能量Airy光束在频域的傅里叶谱[1]可以表示为:exp(-αω2)exp[i(ω3-3α2ω-iα3)/3],其中ω是频域归一化的波数。在频域上移动高斯光束,其傅里叶谱变为exp[-α(ω-ωG)2]×exp[i(ω3-3α2ω-iα3)/3],而ωG表示高斯光束在频域的归一化位移。因此产生的1-D有限能量Airy光束新的电场包络φ1(sx,z)[15]为:
论欧盟家事诉讼中的不方便法院原则——以Chind and Family Agency案为中心…………………………………………………刘 阳(6):72

(3)

(4)
从式(3)可以看出,1-D有限能量Airy光束新的峰值强度位置为ξ-2ωG=0,当ωG=0时,在z=0处光强最大;当高斯光束的位移ωG≠0时,对峰值强度的位置产生变化,所以在频域移动高斯光束对1-D Airy光束的强度分布会产生影响。

Φ1(sx,sy,ξ)=φ1(sx,sy,ξ)+φ1(sx,-sy,ξ)+
φ1(-sx,sy,ξ)+φ1(-sx,-sy,ξ)
(5)
2 数值仿真
2.1 2-D Airy光束峰值强度的调控
典型的Airy光束生成系统如图2所示。高斯光束首先由液晶空间光调制器加载的相位图调制,然后通过傅里叶变换透镜,焦距为f,在傅里叶透镜的后焦面上生成Airy光束。通常高斯光束、相位图和傅里叶透镜被设置为沿z轴同轴,在傅里叶透镜的后焦面放置CCD相机,用于记录Airy光束的强度模式。如图3所示,可通过在液晶空间光调制器上加载2-D Airy光束的相位图,在傅里叶透镜的后焦面上生成2-D Airy光束。图中红点表示高斯光束的位置。

图2 Airy光束生成系统示意图Fig.2 Schematic diagram of Airy beam generation system

图3 单个2-D Airy光束相位图及高斯光束在频域的位置示意图Fig.3 2-D Airy beam phase diagram and the position of Gaussian beam in frequency domain
根据式(3)和式(4),对高斯光束在频域位移对2-D Airy光束强度的影响进行仿真分析。图4为不移动高斯光束(DG,x=DG,y=0),2-D Airy光束分别在z为0 mm、125 mm、190 mm、250 mm时,光束强度仿真以及对应的3-D图。仿真参数设定为:高斯光束波长λ=1550 nm,x0=80 μm,y0=80 μm,α=0.01,c=0 mm。
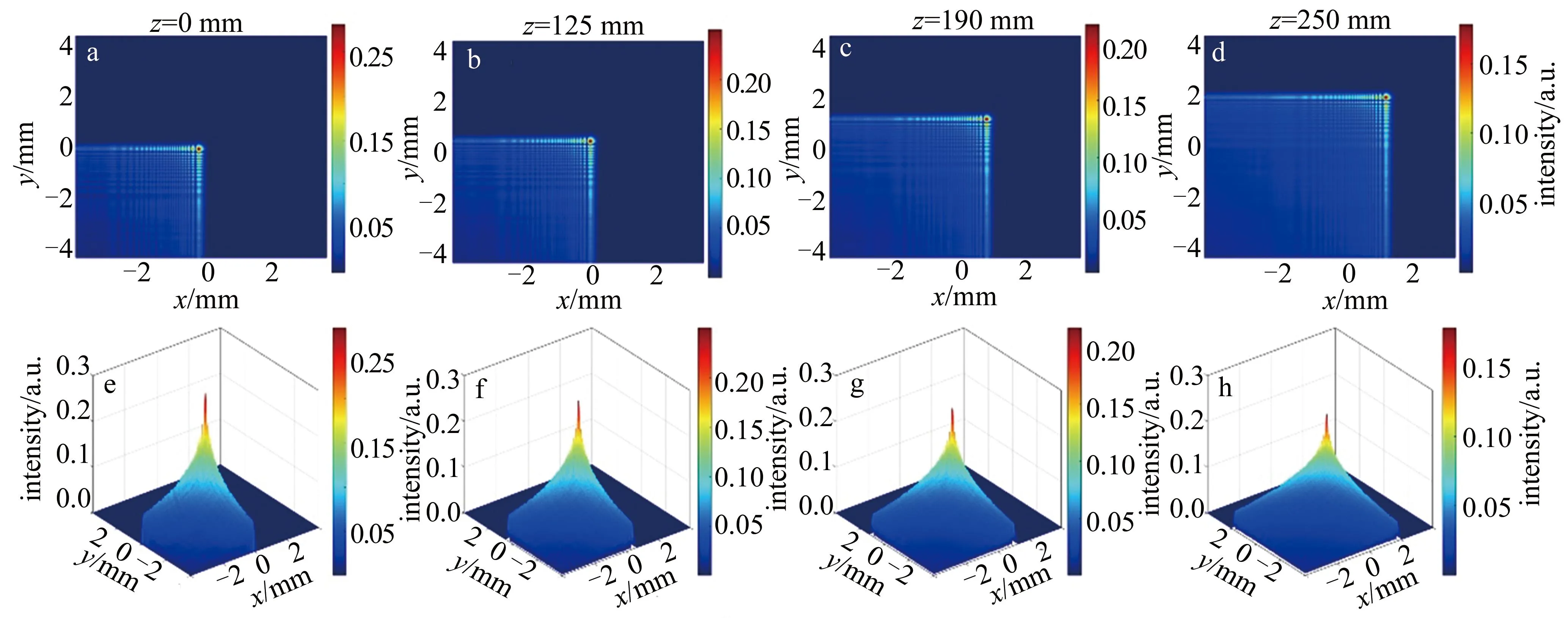
图4 高斯光束无位移时的2-D Airy光束强度Fig.4 Intensity of 2-D Airy beam without Gaussian beam displacement
如图4a所示,当在频域不移动高斯光束(DG,x=DG,y=0)时,z=0 mm处无衍射峰值光束强度为0.28,此时2-D Airy光束强度最强;如图4b所示,2-D Airy光束传播到z=125 mm时,2-D Airy光束强度为0.25,光束强度衰减约10%,2-D Airy光束仍可无衍射传播一段距离;如图4c所示,2-D Airy光束传播到z=190 mm时,2-D Airy光束强度为0.21,光束强度衰减约25%,此时光束强度衰减超过无衍射传播距离的18%,对于在激光通信应用研究中,光束强度受大气湍流影响[23-27],接收端光束强度减弱,影响信号的接收;如图4d所示,2-D Airy光束传播到z=250 mm时,2-D Airy光束强度为0.17,相较于图4a,此时光束强度衰减了约40%。从图4e~图4h的3-D仿真图可以明显地看出,随着传播距离的增加,2-D Airy光束强度在衰减。通过对高斯光束在频域的位移仿真了2-D Airy光束峰值强度位置的变化,在激光通信应用中,可以在一定距离内使峰值光束强度传播到接收端。
图5为移动高斯光束(DG,x=DG,y=4),2-D Airy光束分别在z为0 mm、125 mm、190 mm和250 mm时,光束强度仿真以及对应的3-D图。将初始光强衰减18%时的传输距离,作为2-D Airy光束的无衍射传输距离[23]。如图5a所示,当移动高斯光束(DG,x=DG,y=4)时,在z=0 mm处峰值光束强度为0.20,与图4a相比,光束强度衰减,峰值光束强度的位置发生了改变,不再位于初始距离处;如图5b所示,调控后的2-D Airy光束传播到z=125 mm时,此时2-D Airy光束强度为0.26,光束强度随传播距离的增加而增加;如图5c所示,在z=190 mm时,2-D Airy光束强度为0.28,恢复峰值光束强度,通过高斯光束在频域的位移实现了2-D Airy光束峰值强度位置的变化,利用高斯光束的位移调控,可以将峰值强度传播到目标点;如图5d所示,调控后的2-D Airy光束传播到z=250 mm时,2-D Airy光束强度为0.27,仍然保持了2-D Airy光束的特性,可在此基础上继续无衍射传播一段距离。从图5e~图5h对应的3-D仿真图可以明显地看出,高斯光束位移后2-D Airy光束峰值强度位置的变化,并且峰值光强恢复后2-D Airy光束继续无衍射传播,不影响2-D Airy光束的特性。

图5 高斯光束有位移时的2-D Airy光束强度Fig.5 Intensity of 2-D Airy beam with Gaussian beam displacement


图6 高斯光束的不同位移对2-D Airy光束强度影响Fig.6 Effect of different displacements of Gaussian beam on the intensity of 2-D Airy beam
2.2 2-D Airy光束阵列的初始强度及自聚焦特性

图7 2-D Airy光束阵列的相位图Fig.7 Phase diagram of 2-D Airy beam array
根据式(5)对2-D Airy光束阵列自聚焦过程进行仿真,c=1 mm,DG,x=DG,y=0,如图8所示。图8分别是z为0 mm、125 mm、180 mm和190 mm时,2-D Airy光束阵列强度的仿真以及对应的3-D图,可以更直观地对光束强度进行观察。

图8 2-D Airy光束阵列自聚焦过程示意图Fig.8 Schematic diagram of the self-focusing process of 2-D Airy beam array
图8a在z=0 mm处,2-D Airy光束阵列的4个2-D Airy光束主瓣都指向阵列中心,且每个主瓣中心到阵列中心的距离相同,从图8a对应的3-D图可以看出,每个2-D Airy光束强度为0.28,与图4a中2-D Airy光束在z=0 mm时的光束强度一致,2-D Airy光束阵列中的单个2-D Airy光束仍然保持了2-D Airy光束的特性。
图8b为传播一段距离后,在z=125 mm处的光束聚焦情况,可以看出,相较于在z=0 mm,光束间隔变小,但光束还未接触,4个2-D Airy光束仍保持各自的光学特性,继续向阵列中心传播。将图8e和图8f做比较,在传播125 mm后,因2-D Airy光束的无衍射性,在聚焦之前,4个2-D Airy光束基本保持其初始强度。
如图8c所示,在光束传播到z=180 mm时,4个2-D Airy光束相互接触,但还未融合;如图8g所示,此时Airy光束阵列强度还未突增。
如图8d所示,在光束传播到z=190 mm时,4个2-D Airy光束相互融合完成了自聚焦,此时光束强度突增为0.56,与图4c和图5c相比,实现了2-D Airy光束阵列强度在焦点的提高。此时,在经过4个2-D Airy光束传输一段距离后实现的自聚焦光束初始强度为0.85。
2.3 2-D Airy光束阵列焦点处强度的调控
从图4和图5可以看出,通过对高斯光束在频域的位移调控,仿真实现了2-D Airy光束峰值强度位置的变化;从图8可以看出,2-D Airy光束阵列的自聚焦可以在焦点实现光束强度的突增,相比单个2-D Airy光束强度更高,但在焦点完成自聚焦之前,阵列中每个2-D Airy光束仍要传播一段距离才能完成自聚焦,随着阵列中每个2-D Airy光束的传播,光束强度会损失一部分,通过对高斯光束在频域的位移调控可实现2-D Airy光束阵列焦点的强度的增强。图9为高斯光束在2-D Airy光束阵列频域的位移示意图。图中红点表示高斯光束的位置,箭头表示高斯光束的位移方向。

图9 高斯光束在2-D Airy光束阵列频域的位移示意图Fig.9 Schematic diagram of the displacement of Gaussian beam in frequency domain of 2-D Airy beam array
在频域移动高斯光束时,2-D Airy光束阵列各象限光束强度调控的仿真结果如图10所示。在第一象限沿45°方向移动高斯光束(DG,x=DG,y=d,d>0),当高斯光束发生位移时,对于4个象限中每个2-D Airy光束的位移都不同。下面首先仿真了高斯光束位移(DG,x=

图10 高斯光束位移DG,x=DG,y=1时,2-D Airy光束阵列各象限强度的仿真Fig.10 Intensity of each quadrant of 2-D Airy beam array at Gaussian beam displacement DG,x=DG,y=1
DG,y=1)时,在z=0 mm初始平面处,对每个象限中的2-D Airy光束强度的影响,图10分别是2-D Airy光束阵列在第一象限、第二象限、第三象限、第四象限的光束强度仿真图,以及对应的2-D Airy光束阵列强度的3-D图。
如图10所示,高斯光束位移DG,x=DG,y=1时,第一象限的2-D Airy光束强度为0.281;第二象限2-D Airy光束强度为0.270;第三象限2-D Airy光束强度为0.259;第四象限2-D Airy光束强度为0.271,高斯光束位移对2-D Airy光束阵列中的每个光束强度产生不同的影响,从而在频域位移不同距离的高斯光束对焦点处自聚焦的2-D Airy光束阵列强度产生不同影响。
通过高斯光束的位移可以控制2-D Airy光束阵列焦点的强度,图11为移动高斯光束,即(DG,x,DG,y)取不同值时,在z=190 mm 2-D Airy光束阵列自聚焦处,Airy光束阵列强度的仿真结果以及对应的3-D仿真结果。

图11 高斯光束位移后2-D Airy光束阵列焦点的强度仿真Fig.11 2-D Airy beam array intensity in focus simulation after Gaussian beam displacement
从图8d可以看出,在不移动高斯光束,即DG,x=DG,y=0、z=190 mm时,2-D Airy光束阵列强度为0.85。
如图11a所示, 移动高斯光束,DG,x=DG,y=1,2-D Airy光束阵列自聚焦强度为0.96;如图11b所示,DG,x=DG,y=2,2-D Airy光束阵列自聚焦强度为1.04;如图11c所示,DG,x=DG,y=3,2-D Airy光束阵列自聚焦强度为1.1。随着高斯光束的移动,对焦点处自聚焦的2-D Airy光束阵列强度进行了调控,实现了2-D Airy光束阵列强度的增强。
因2-D Airy光束阵列中每个光束在自聚焦之前保持了Airy光束的光学特性,通过高斯光束位移对每个2-D Airy光束强度的调控,实现了2-D Airy光束阵列焦点处强度的调控,在2-D Airy光束阵列焦点固定的情况下,可灵活方便地对2-D Airy光束阵列强度进行调控,且过程简单。
2.4 模拟大气湍流条件下2-D Airy光束阵列强度调控的效果
因Airy光束的无衍射特性,对大气湍流具有一定的抑制能力,2-D Airy光束阵列强度的调控使焦点汇聚的能量更强,为光束抵抗大气湍流提供了一种新的方法,通过模拟2-D Airy光束阵列强度在大气湍流中的调控,分析了此方法对2-D Airy光束阵列光强的影响,如图12所示,模拟了湍流条件下2-D Airy光束阵列强度调控的效果。

图12 中等湍流条件下,2-D Airy光束阵列焦点强度的仿真图Fig.12 Simulation of focal intensity of 2-D Airy beam array under moderate turbulence conditions
通过功率谱反演法生成随机湍流相位屏,将2-D Airy光束阵列通过生成的随机湍流相位屏,进行大气湍流的强度仿真,仿真参数为:大气折射率结构常数Cn2=8×10-14m-2/3,x0=11 mm,y0=11 mm,λ=1550 nm,c=1 mm,α=0.01,光束在1 km处聚焦。图12为中等湍流强度下,在z=1 km 2-D Airy光束阵列自聚焦处,Airy光束阵列强度仿真图以及对应的3-D仿真结果。如图12a所示,没有湍流、不移动高斯光束、DG,x=DG,y=0和z=1 km时,2-D Airy光束阵列强度为1.09;此时在不移动高斯光束的情况下,加入湍流,光束强度仿真结果如图12b所示,2-D Airy光束阵列强度为0.85,因为大气湍流的影响,光束强度降低;通过移动高斯光束,使DG,x=DG,y=1.43,如图12c所示,在z=1 km处,加入湍流的情况下,2-D Airy光束阵列自聚焦强度增强为1.03,提高了2-D Airy光束阵列抵抗大气湍流的能力,使光束在焦点处的强度增强。
3 结 论
理论分析了2-D Airy光束阵列焦点处强度调控的原理,并对其进行了仿真研究。通过仿真发现:在高斯光束的调控下,2-D Airy光束峰值强度可以由初始位置z=0 mm处调控到z=190 mm处,实现了对2-D Airy光束峰值强度位置的调控;在2-D Airy光束峰值强度调控的基础上,对2-D Airy光束阵列焦点处的强度实现了增强,在未调控的情况下,2-D Airy光束阵列焦点处的初始光强为0.85,经过高斯光束在频域的调控,焦点处的光强增加为1.1,实现了2-D Airy光束阵列焦点处强度的增强;大气湍流条件下,通过强度调控,在z=1 km处2-D Airy光束阵列强度由0.85增强到1.03,对抵抗大气湍流具有一定的作用,在激光通信增强接收端信号方面具有重要的研究价值。

