鱼眼成像系统标定技术研究

王云鹏,刘力双,刘 洋

(北京信息科技大学 仪器科学与光电工程学院,北京 100192,中国)

0 引 言

鱼眼镜头是一种特殊的广角镜头,具有较广阔的视野范围和较短的焦距[1-3]。大视角的特点使鱼眼镜头在红外地球敏感器和广角侦查系统等众多领域得到广泛的应用。然而,鱼眼镜头自身工艺制作的缺点以及镜头在组合装配中的误差使其不可避免地引起了图像畸变[4-5],图形畸变的产生会在提取目标方位信息时造成偏差。方位信息的偏差在红外地球敏感器中,会造成地平圆圆心目标的定位不精确,无法准确计算卫星的姿态信息;在广角侦查系统中,同样会导致系统在对目标定位时出现偏移,使目标定位精度下降。如何通过畸变图像在大视场鱼眼成像系统中确定目标的方位,成为了近年来国内外众多学者深入研究的重点问题。

根据鱼眼图像精确提取目标方位的本质是建立2维图像和3维空间的映射关系[6]。TSAI的两步法[7]和ZHANG的棋盘标定法[8]虽然具有较高的标定精度,但需要尺寸与大视场成像系统拍摄范围相匹配的标定板,制作成本较高,实验难度较大。ZHU等人[9]建立球面投影模型,基于畸变参数分离的思想标定鱼眼成像系统,但该模型中要确定的畸变参数过多,导致计算量过大。XIAO等人[10]采用两步法模型,分别对靠近光学中心的区域建立线性畸变模型和远离光学中心的区域建立非线性畸变模型,实现对目标转台姿态角的精定位,但经实验验证,其所提出的坐标轮转方法不能精确定位光学中心,影响转台姿态角的拟合精度。

为提升在大视场鱼眼成像系统中目标定位精度,本文作者采用了基于相机移动的研究方法构建鱼眼成像系统的标定模型。控制高精度2维旋转位移台的角度位置,移动鱼眼成像系统拍摄固定位置的点光源,根据点光源在鱼眼成像系统中的方位角度和光点在图像中的像素位置,构建两者之间的数学模型。为提高模型标定精度,减小系统标定误差,采用图像有效区域的边缘拟合圆计算出光学中心,并采用分区域标定的方式计算出畸变参数。再根据像素位置拟合标定物方位角度,验证模型精度。

1 标定原理

1.1 鱼眼成像系统成像模型

如图1所示,在鱼眼成像系统中,成像的过程就是3维世界坐标系下点Pw经一系列坐标变化映射成为2维图像坐标系下点Pd的过程[11]。具体过程为:世界坐标系(xw,yw,zw)下的点经过光线映射到摄像机坐标系(xc,yc,zc)中,再投影到代表传感器的成像平面坐标系(x,y)上,最终经过数模变换映射为图像坐标系(u,v)中的像素点[12]。

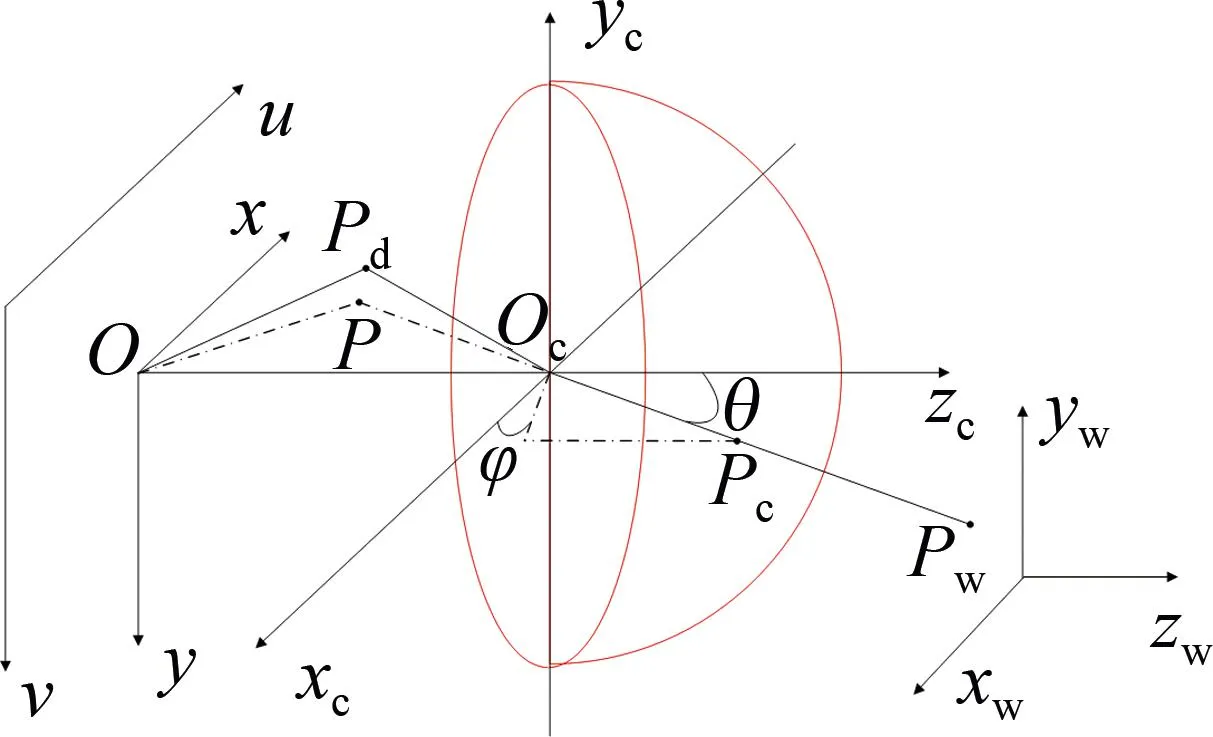
图1 鱼眼镜头成像模型Fig.1 Fisheye lens imaging model

在摄像机坐标系下,将鱼眼镜头视作半径为R的半球面。经世界坐标系中任一点Pw的光线沿光学中心的方向进入摄像机坐标系,交点为Pc(xc,yc,zc),入射角为θ,在xcyc平面上的投影与xc轴正方向的偏移角为φ,Pc点可以由θ和φ确定:

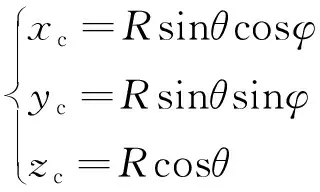
(1)

根据小孔成像原理,Pc在图像平面的理想投影为点P(u,v),两者之间的坐标映射关系为:

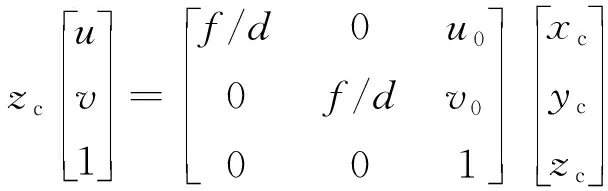
(2)

式中:(u0,v0)为光学中心Oc在图像平面上投影O的像素坐标;f为鱼眼镜头焦距;d×d为单个像元尺寸。

鱼眼成像系统的结构不同于一般成像系统,主要受非线性畸变影响,成像多为非相似成像。Pc在图像平面的实际投影为点Pd(ud,vd),P点与Pd点间的畸变关系将在下一节中进行讨论。

根据式(1)和式(2),得到在鱼眼镜头坐标系下入射角θ与图像平面下点P到光学中心距离r之间的关系:

tanθ=A×r

(3)

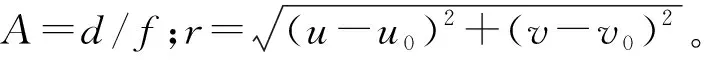
同理,也得到偏移角φ与P点像素坐标之间的关系:

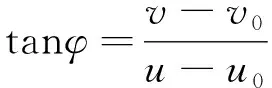
(4)

1.2 目标方位角与像素间的标定模型

在鱼眼成像系统中,点Pc本该于理想成像点P处成像,但因为成像过程受到非线性畸变的影响,实际成像位置偏移到了点Pd处,如图2所示。这种成像点的位置偏移是无法精确提取目标方位的主要原因,受到径向畸变、切向畸变和薄棱镜畸变三者的影响,其中薄棱镜畸变的影响过小可将其忽略[13-14],主要考虑前两者的影响。径向畸变是造成图像畸变的主要原因,表现为成像点在半径方向上发生位置偏移,产生原因是生产工艺造成鱼眼镜头表面出现不规则的形状[15]。径向畸变模型为:

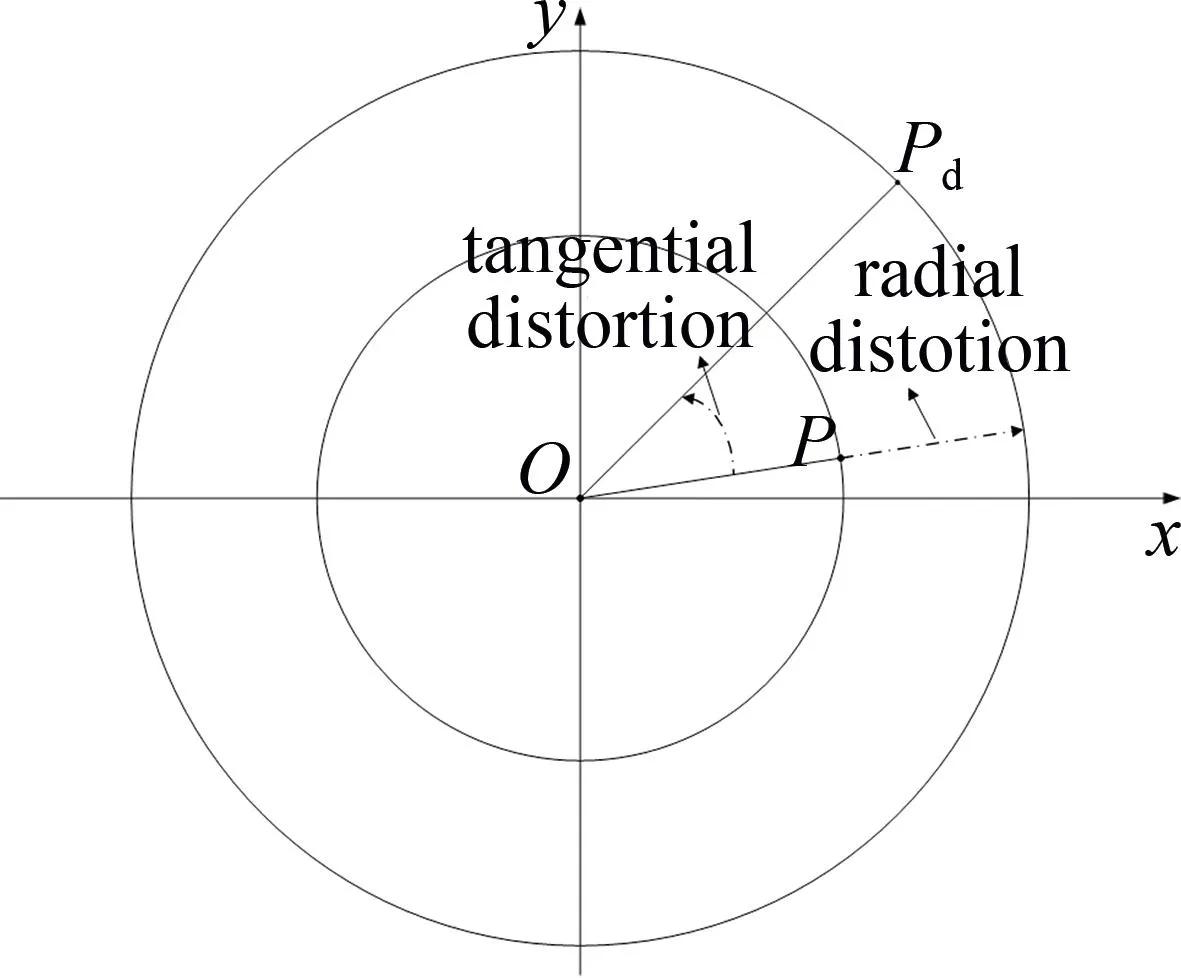
图2 非线性畸变成像点偏差Fig.2 Nonlinear distortion imaging point deviation

r=k1×rd+k2×rd3+k3×rd5

(5)

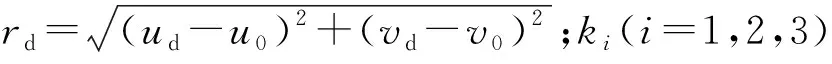
切向畸变改变了成像点到光学中心矢量的角度,使成像点发生角度偏转。产生原因是构成鱼眼镜头透镜的光心与几何中心不重合[16],畸变模型为:

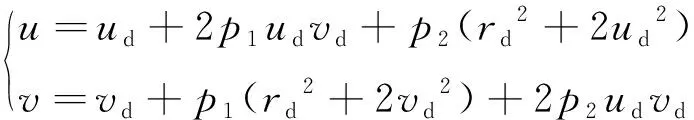
(6)

式中:pj(j=1,2)为切向畸变参数。

将式(5)代入式(3)可得:

tanθ=K1×rd+K2×rd3+K3×rd5

(7)

式中:入射角畸变参数Ki=A×ki,i=1,2,3。

将式(6)代入式(4)可得:

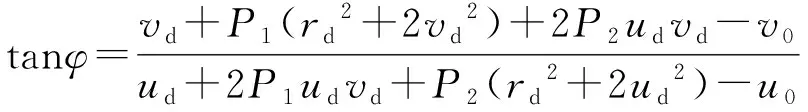
(8)

式中:偏移角畸变参数Pj=pj,j=1,2。

将标定点的入射角θ集合与距光学中心的距离rd集合代入式(7)中,即可求得入射角畸变参数Ki(i=1,2,3)。同理将标定点的偏移角φ的集合与像素坐标Pd(ud,vd)集合同时代入式(8)中,即可求得偏移角畸变参数Pj(j=1,2)。

1.3 光学中心计算

1.3.1 图像有效区域边缘拟合光学中心 鱼眼成像系统的畸变围绕光学中心对称,畸变程度与成像点离光学中心的距离为正相关[17]。理想情况下光学中心的成像位置应该与图像中心相重合,但由于鱼眼镜头的装配误差,使得两者不能完全重合,需要对其单独标定[18-19]。因为大视角的特点,鱼眼图像成像有效区域边缘为圆形。为计算出光学中心,选择采用最小二乘法拟合鱼眼图像的有效区域边沿圆,拟合得到的圆心就是光学中心的实际像素位置。设理想圆的标准方程为:

(xs-a)2+(ys-b)2=r2

(9)

式中:(xs,ys)为圆上的任意一点;(a,b)为圆心坐标;r为圆的半径。

最小二乘法要求残差值最小:

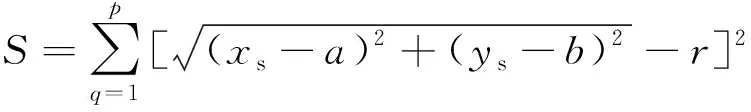
(10)

当残差值S最小时,则有:

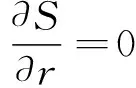
(11)

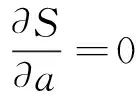
(12)

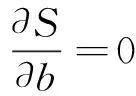
(13)

根据以上3式,可以求出圆心(a,b)和半径r。

1.3.2 亚像素边缘检测 在进行最小二乘法拟合前,采用了亚像素边缘检测算法中的灰度矩边缘定位法定位图像有效区域轮廓,提升光学中心的拟合精度从而减小系统的标定误差。基本原理是假设图像的实际边缘分布与阶跃式变化的理想边缘的灰度矩一致[20],利用图像实际边缘的前3阶灰度矩求取图像的亚像素边缘点。

设鱼眼图像实际边缘的灰度值为hl(l=1,2,3,…,n);n为图像实际边缘包含的像素点总数,计算图像的图像实际边缘的前3阶灰度矩:

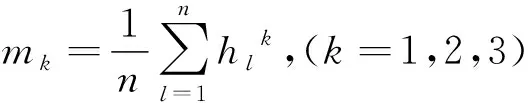
(14)

得到前3阶灰度矩后,精确计算图像的亚像素边缘点的位置:

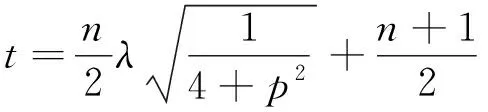
(15)

式中:λ=(m3+2m13-3m1m2)/(m2-m12)2/3。

通过传统边缘检测算法粗定位图像边缘的像素坐标(xe,ye),根据周围像素点的灰度值判断边缘方向:当Gx>Gy(Gx和Gy分别表示边缘在x方向和y方向的梯度算子),边缘方向为水平;反之,边缘方向为垂直。

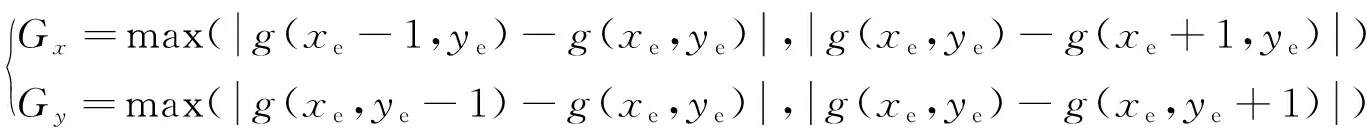
(16)

式中:g(xe,ye)为点(xe,ye)的灰度值。

得到边缘方向后,以(xe,ye)为中心,延灰度方向分别向两侧拓展6个像素,根据式(15)求得亚像素边缘点。

1.4 分区域标定法

鱼眼镜头产生的畸变是非线性的畸变,图像中不同位置的像点受到的畸变影响程度不同,用同一组畸变参数对整幅图像校正,对校正精度和稳定性会产生影响[21]。为了能提高标定精度,对鱼眼图像采取了一种分区域标定的方法,对不同区域求取不同的畸变参数,提升标定的精度。

在鱼眼成像系统中,成像点到光学中心的距离主要受标定物入射角θ影响。鱼眼图像的畸变关于光学中心对称,且随着成像点距光学中心距离的增大而增加,在以光学中心为圆心的圆上畸变大致相同[22]。如图3所示,在标定过程中,根据标定物入射角θ的大小将鱼眼图像划分为以光学中心为圆心的同心圆区域,对每个区域进行标定。

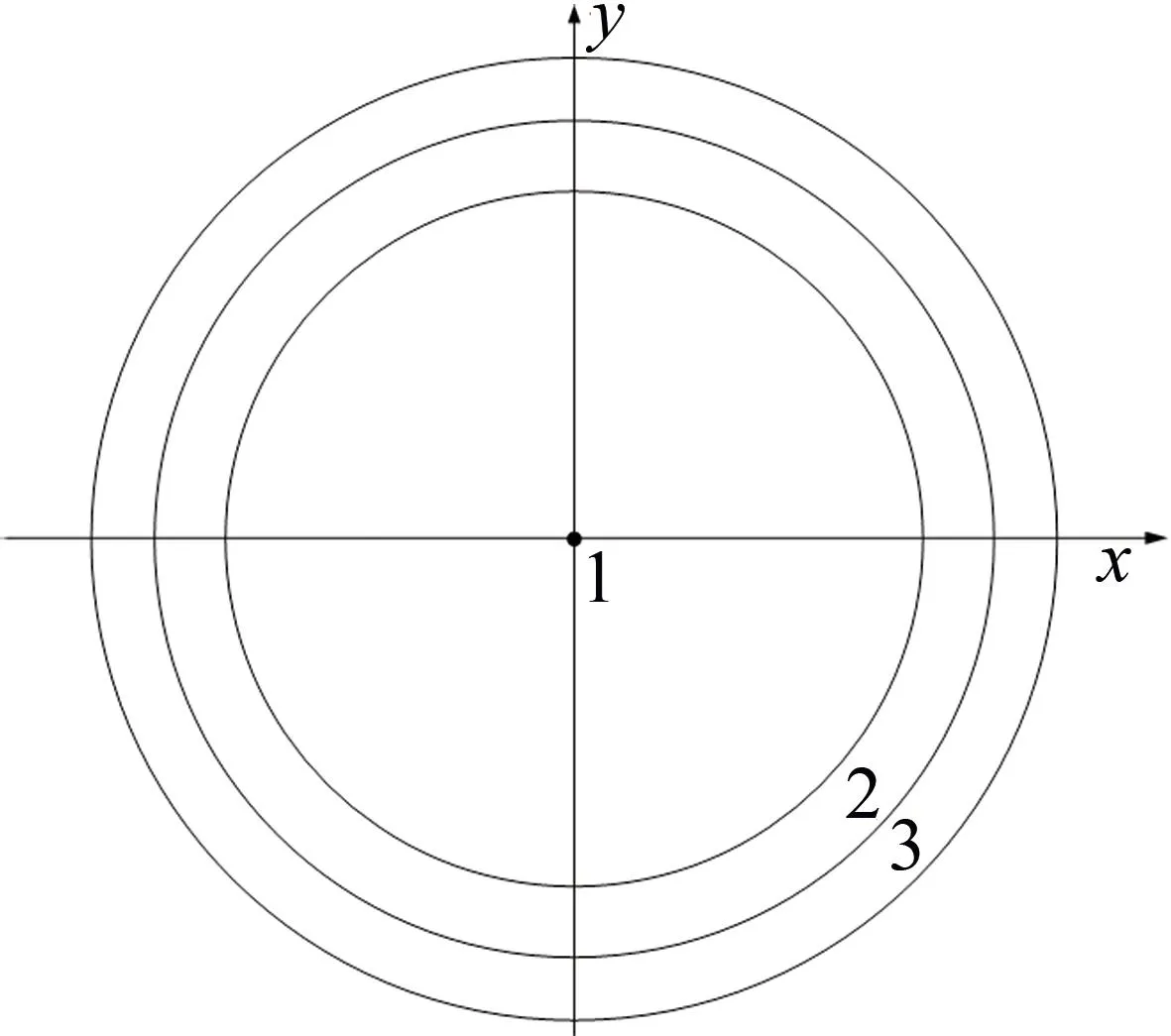
图3 标定区域划分示意图Fig.3 Marking area division diagram

2 实验及结果分析

2.1 搭建实验系统

实验系统由图像采集和方向控制两部分组成。图像采集部分由中联科创鱼眼镜头VM0420MP5、大恒工业相机DH-HV1351UM和标定物做成,标定物是单个点光源,相机分辨率为1280 pixel×1024 pixel。方向控制部分是由高精度2维旋转位移台、光学平台和上位机组成,上位机可以对转台实现精确控制,角度变化精度为0.004°。图4为实验系统搭建的示意图,图5为实验系统实物图。

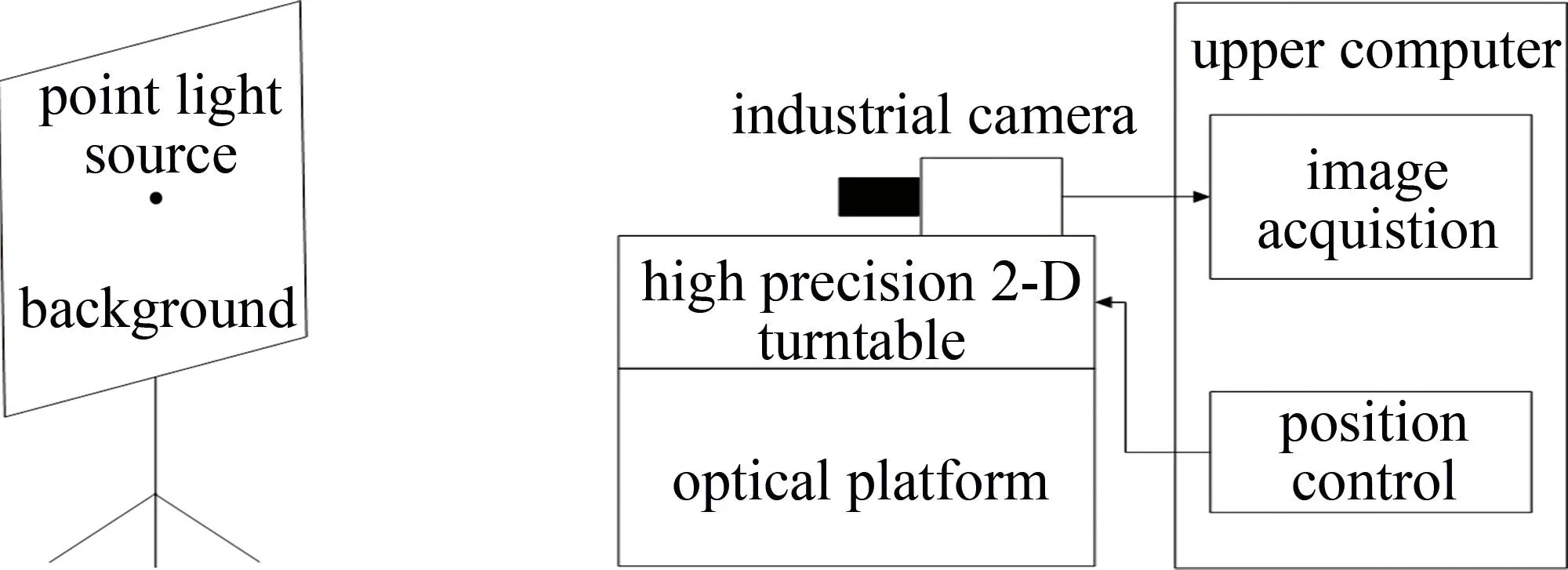
图4 实验系统搭建Fig.4 Experimental system construction

图5 高精度2维转台及鱼眼成像系统实物图Fig.5 Physical view of high precision 2-D turntable and fisheye imaging system

2.2 计算光学中心

控制鱼眼成像系统拍摄多幅白纸的图像。根据前面提出的灰度矩边缘定位法提取图像有效区域的边缘,对提取到的边缘使用最小二乘法拟合,得到鱼眼图像光学中心的坐标(a,b)和半径r。图6所示为亚像素边缘检测结果。

图6 亚像素边缘检测Fig.6 Sub-pixel edge detection

拍摄8组图像进行拟合,如表1所示,为对8组数据的拟合结果。取结果的平均值(651.51 pixel,525.57 pixel)作为光学中心和619.36 pixel作为有效区域半径。

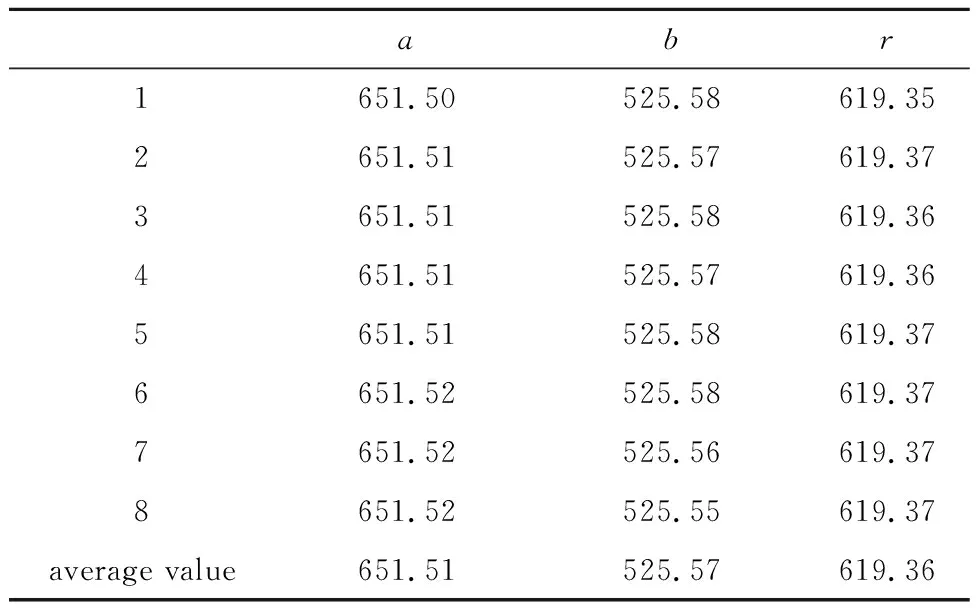
表1 光学中心及图像有效区域半径拟合结果/pixelTable 1 Optical center and image effective area radius fitting results/pixel

2.3 实验数据采集

标定物单个点光源由红色平板光源和带孔的不锈钢板组合构成,将不锈钢板覆盖于平板光源表面。孔洞为直径10 mm的圆孔,钢板厚度为0.1 mm,在钢板外侧表面覆盖遮挡物,只留下作为点光源的孔洞,这样得到的点光源较为均匀,光源边缘成像效果更为清晰。标定物在鱼眼成像系统中的成像近似为圆形,面积约为116 pixel,在对图像进行均值滤波后,通过灰度质心法提取标定物中心作为标定点。图7为标定物在初始位置的图像。

图7 标定物在初始位置成像Fig.7 Imaging of the calibrator at the initial position

控制高精度2维旋转位移台,调整角度位置,使标定点与鱼眼成像系统的光学中心相重合,此位置为鱼眼成像系统的初始位置。然后移动鱼眼成像系统,在不同角度下拍摄标定物,记录标定点在图像中的像素坐标(u,v)和标定物在鱼眼成像系统的方位角度(θ,φ)。共拍摄图像184幅,使标定点尽可能充满整个图像。将采集到标定物的方位角度和图像点的像素坐标作为数据集代入式(7)、式(8),计算出畸变模型。

图8为标定物在不同方位的成像。为了验证标定精度通过转台转动鱼眼成像系统到任意角度,拍摄10幅图像。计算出每幅图像中标定点的像素坐标及到光学中心的距离,将这些数据作为测试集代入畸变模型中,拟合每幅图像中标定物的方位角度,与实际方位角度θ和φ对比,检测系统标定精度。

图8 不同方位标定物成像Fig.8 Imaging of calibrators in different orientations

2.4 实验结果

在实验中采取分区域标定的方式以降低系统的标定误差,根据入射角度θ划分区域。为了降低标定系统的复杂性,采用三区域划分法。在划分区域时,要保证各区域的标定误差尽可能的小,且每个区域的数据集点不能过少,影响畸变参数的求取,所以采取角度遍历的方式分别对两个分界角度进行求取,先根据各区域数据集求取畸变模型,再将测试集代入畸变模型,计算标定精度。

经过测试,入射角θ的最大值为90°。先求取区域1、2的分界角度,在区间[30°,80°]中,采用步进为1°进行遍历,找到能使区域1中标定误差最小的角度,角度为42°;再根据求取的第1个分界角度,重新划分区间[50°,80°],求取区域2、3的分界角度71°,使二区域的标定误差最小。

根据求得角度进行区域划分,验证理论。单区域为图像的整个视场;二区域以42°为界线划分区域1(0°～42°)、区域2(42°以上);三区域划分为区域1(0°～42°)、区域2(42°～71°)、区域3(71°以上)。根据采集数据分别计算各区域的畸变参数和标定误差,如表2和表3所示。

表2 分区域畸变参数Table 2 Sub-regional distortion parameters

表3 实验结果Table 3 Experimental result

根据实验结果可知,拟合标定物方位角度的误差值随着标定区域的增加而减小。在将整个鱼眼图像划分为3个区域时,区域1的平均误差为0.06°,区域2的平均误差为0.26°,区域3的平均误差为0.45°。可以看出,靠近光学中心的主要成像区域误差较小,远离光学中心的边缘成像区域误差较大,对鱼眼图像划分区域标定可以有效降低系统的标定误差,提升了整个鱼眼成像系统的标定精度。

3 结 论

为了提升大视场鱼眼成像系统中目标定位精度,采用基于相机移动的研究方法构建鱼眼成像系统的标定模型。先计算光学中心坐标,再对鱼眼图像进行分区域标定,依据标定点像素位置拟合其在大视场中的方位。相较于其它标定算法需要先校正图像再求取目标方位,本文中所提出的方法通过模型直接将像素点与空间坐标建立了对应关系,同时对其它参数如焦距等不做关心,降低了标定的复杂程度。另外,采用点光源加相机转台的方法,也避免了制造高精度大尺寸标定板,降低了系统的复杂性和成本。

从实验结果来看,分区标定方法避免了一套畸变系数造成的部分区域误差过大的问题,既保证了图像中心区域的精度,又提高了容易造成大误差的大视角区域的精度。在划分为三区域标定时,可以将靠近光学中心的主要成像区域的平均误差降低到0.06°,相比于前文提到的其它算法,拥有更高的标定精度。这一标定方法可以应用到红外地球敏感器、广角侦查系统等领域的大视角应用场景中对鱼眼成像系统进行的标定。