模分复用系统中盲均衡算法的均衡性能研究

王 芳,延凤平*,秦 齐,常 欢,任文华

(1.北京交通大学 电子信息工程学院,北京 100044,中国;2. 北京理工大学 信息与电子学院,北京 100081,中国)

0 引 言

随着5G、大数据和云计算等现代技术的快速发展[1],全球互联网流量正在急速增长。由于传统单模光纤的非线性效应,其系统容量已达到香农极限[2],不能应对目前的“容量危机”,因此必须寻找新的复用维度,即空间维度。空分复用在光纤领域的主要实现技术方法有两种,即基于多芯光纤的空分复用技术[3-4]和基于少模光纤的模分复用技术[5-6]。基于少模光纤的模分复用技术可以极大地扩展通信容量,但同时传输过程中会出现模式耦合、差分模式群时延(differential mode group delay,DMGD)、色散等问题,从而影响接收数据的准确性[7-8]。将无线领域的多输入多输出(multiple-input multiple-output,MIMO)均衡[9-10]思想引入光纤领域,可以有效解决这一问题。常用的MIMO均衡算法有递推最小二乘法(recursive least square,RLS)算法、最小均方(least mean square,LMS)算法和恒模算法(constant modulus algorithm,CMA),RLS和LMS是非盲均衡算法,需要训练序列,而CMA是盲均衡算法,不需要训练序列。CMA根据发送信号的统计量就可迭代更新均衡器的抽头系数,实现信号的恢复,这是它的一大优势。CMA被广泛应用于恒模信号[11],效率高、实时性好、具有良好的收敛性[12]。

目前已有大量的工作研究CMA算法在各类系统中的应用。例如,ZHANG等人[13]在典型的电话信道上研究比较CMA和变步长CMA的性能,变步长CMA能较好地平衡收敛速度和剩余误差。XUE等人[14]在无线信道上比较CMA和修正的恒定模数算法(modified constant modulus algorithm,MCMA)的均衡效果,结果表明,MCMA可以加快收敛速度。QIN等人[15]研究CMA对100 Gbit/s 双偏振正交相移键控(dual-polarization quadrature phase shift keying,DP-QPSK)光信号传输系统中色散的补偿作用,证明该算法具有良好的收敛性能和收敛速度。JIN等人[16]建立2×2的弱耦合少模复用系统,并利用频域CMA和MCMA算法进行均衡,结果表明,频域CMA和MCMA算法均适用于模分复用系统的均衡,并且频域MCMA的均衡性能优于频域CMA。不同于参考文献[16],本文中采用强耦合6模复用系统,发送端模式数增加,需要将时域CMA和MCMA算法扩展为12×12的MIMO结构,另外由于相同滤波器权值和迭代步长下,强耦合使算法收敛难度增大,因此,需要利用传输参数对均衡滤波器进行粗略初始化,并重新调整滤波器权值和迭代步长。

本文作者采用具有强模式耦合的3模光纤作为传输通道。在考虑色散、群延迟和模式串扰的前提下,研究在模分复用系统中CMA和MCMA对输出信号均衡性能的影响,其中传输信号由3个双偏振的正交相移键控信号组成,光纤通道为3模光纤。

1 原 理

经过CMA均衡后的输出信号可能存在一定的相位误差,单独使用时,需要加入相位恢复模块。MCMA可以修正CMA造成的相位旋转,同时能在误比特率方面得到一定改善。本文作者在基于强耦合少模光纤的模分复用系统中比较了CMA和MCMA的均衡效果。接下来分别对两种算法的原理进行介绍。

1.1 CMA

CMA的基本思想[17]如下:恒模信号通过理想光纤信道传输后仍具有恒模特性,但实际的光纤信道存在损耗、色散等损伤,需要使用算法更新均衡器的抽头系数,使信号重新具有恒模特性。

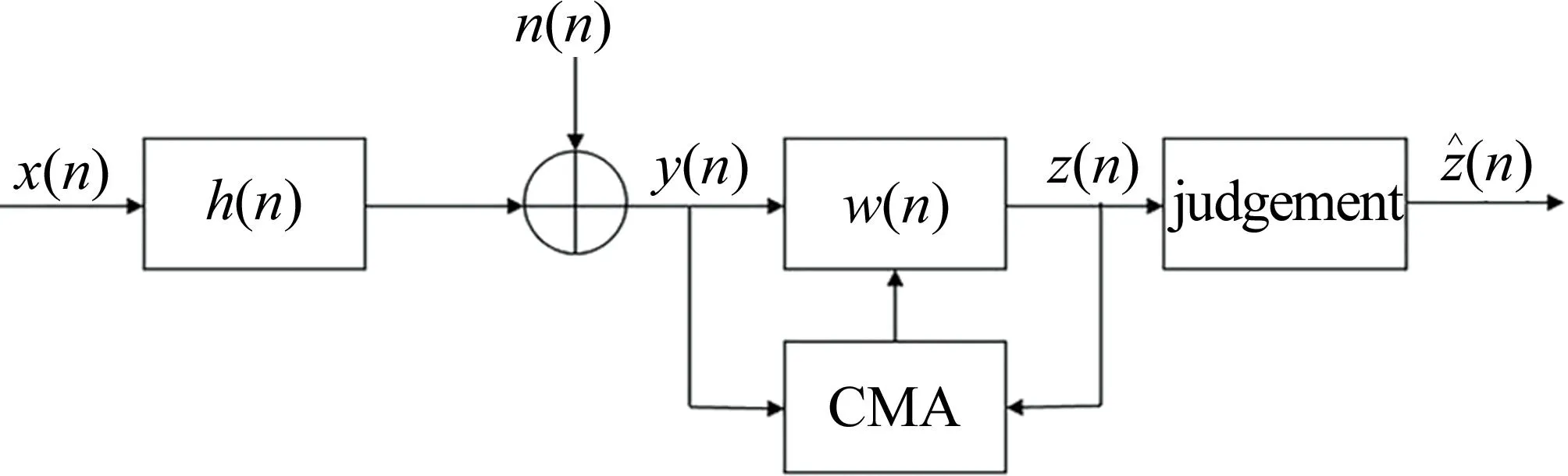
图1 CMA示意图[18]Fig.1 Diagram of CMA[18]

CMA的代价函数为[19]:

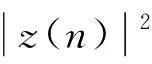
(1)

式中:E[·]是期望函数;R2为CMA模值,是一个常数。R2可表示为:

(2)

由式(1)可知,代价函数只包含了接收信号的幅度信息,没有包含相位信息。因此,发送信号通过复数信道后会出现相位偏移。

误差函数表示为:

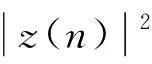
(3)

根据梯度下降法,可得均衡器w(n)的权向量迭代过程如下:

w(n)-μ·e(n)·y*(n)

(4)

式中:μ表示迭代步长;y*(n)表示对y(n)进行共轭运算。CMA的迭代步长μ是常数,其大小决定算法的收敛速度。

1.2 MCMA

MCMA算法的原理是把式(1)的代价函数的实虚部分开,再分别计算[20]:

J(n)=Re(J(n))+Im(J(n))

(5)

其中:

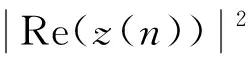
(6)

(7)

式中:Re(·)和Im(·)分别表示实部、虚部。Re(R2)、Im(R2)可以表示为:

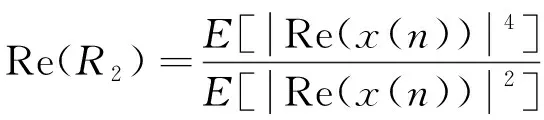
(8)

(9)

误差函数定义如下:

e(n)=Re(e(n))+Im(e(n))

(10)

Re(e(n))=

(11)

Im(e(n))=

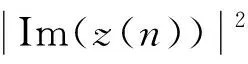
(12)

MCMA的代价函数同时包含信号的幅度和相位信息,能够有效修正信号经过复信道后引起的相位旋转。

1.3 性能指标

收敛速度和均方误差(mean square error,MSE)是盲均衡算法的两个主要性能指标[21],这两个指标都可以从MSE曲线得到。通常情况下,MSE被定义为期望数据和均衡后数据对应点误差的平方和的均值,用σ表示,表达式如下:

(13)

在CMA和MCMA算法中,σ(n)一般定义为|e(n)|。

2 仿真系统结构

为了分析CMA和MCMA的性能,利用VPI仿真软件,基于功率耦合理论搭建了一个3模模分复用系统,系统结构如图2所示。在仿真中,6×56 Gbit/s的DP-QPSK信号通过模式复用器在具有LP01、LP11,a和LP11,b光纤模式的3模光纤中传输,3种模式之间只发生强耦合。该系统的传输距离为80 km,光信号在传输过程中还受到色度色散、偏振模色散和模式群时延的影响,具体参数值如表1所示。最后,信号经过一个放大器和一个模式解复用器,接收机得到受损信号。

表1 参数设置Table 1 Parameter settings

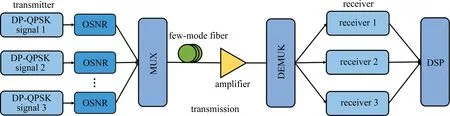
图2 基于少模光纤的模分复用系统Fig.2 Mode-division multiplexing system model based on few-mode fiber

在本次仿真中,激光器线宽被设置为100 kHz。

对于传输后的受损信号需要进行一系列数字信号处理(digital signal processing,DSP),才能恢复原始信号,主要包括模数转换(analog-to-digital converter,ADC)、色散补偿(CD compensation)、MIMO均衡和载波相位估计(carrier phase estimation)。DSP的实现流程如图3所示。其中,MIMO均衡是本文中的研究重点。

图3 DSP流程图Fig.3 Flow chart of DSP

3 仿真结果分析

CMA对接收端的受损信号进行均衡补偿,其中传输信号为DP-QPSK信号,光信噪比(optical signal-to-noise ratio,OSNR)为20 dB。算法的稳态误差大小和收敛速度快慢受迭代步长的影响。图4所示是选择不同迭代步长时CMA的MSE曲线。其中均衡器的长度为122,迭代步长分别为0.0007、0.0005和0.0001。为方便起见,这里只显示LP01,x的MSE曲线。

图4 不同迭代步长的CMA算法曲线图Fig.4 Convergence curves of CMA for different iteration steps

由图4可知,当迭代步长较大时,收敛速度较快,但稳态误差也较大;当迭代步长较小时,稳态误差小,但收敛速度也较慢。因此,在选择迭代步长时,需要在收敛速度和稳态误差之间权衡。

图5所示是使用CMA均衡前后的信号星座图的比较结果。基于上述分析,步长选择为0.0005,均衡器的长度为122。

图5 信号星座图a—均衡前 b—CMA均衡后Fig.5 Signal constellation diagrama—before equalization b—after CMA equalization

图5a描述了均衡前的接收信号的星座图。在色散、模式耦合和模式时延的影响下,6个信号都出现了严重的振幅和相位失真,信号星座点分散,信息无法被有效传输。图5b显示了CMA均衡后信号的星座图。与图5a相比,CMA成功恢复了模式信号。计算了星座图的色散程度,即计算4个相位状态中每个相位的均方根误差(root mean square error,RMSE),结果如图6所示。图6中的数值表明,RMSE值都接近0.2,低于最大值2,可以判断6路模式信号的RMSE值很小,说明数据比较集中。

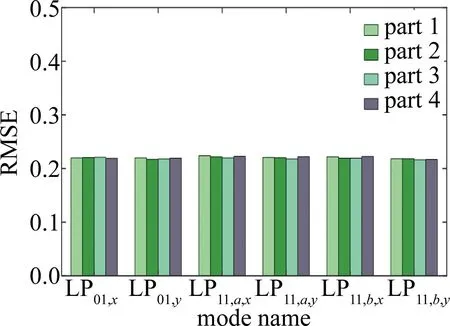
图6 不同模式的RMSE值Fig.6 RMSE values for different modes

下面将MCMA的均衡性能与CMA的均衡性能进行比较,其中传输信号为DP-QPSK信号,OSNR为19 dB,选择的步长为0.0005,均衡器的长度为122。

图7所示是分别使用CMA和MCMA均衡后的MSE收敛曲线。比较结果可知,使用MCMA均衡产生的稳态误差较小。为方便起见,只显示LP11,a,y的MSE曲线。

图7 CMA和MCMA收敛性能的比较Fig.7 Comparison of CMA and MCMA convergence performance

图8a所示是使用CMA均衡后的信号星座图,可以看出,信号基本恢复,但仍有大量散点。图8b所示是使用MCMA均衡后的信号星座图,比较可知,星座图散点减少,信号恢复更理想。

图8 均衡后信号星座图a—使用CMA b—使用MCMAFig.8 Constellation diagrams after equalizationa—with CMA b—with MCMA

接下来,继续用RMSE来衡量CMA和MCMA均衡后的星座图的离散程度,如图9所示。比较图9a和图9b可以看出,MCMA均衡后的信号的离散程度比CMA均衡后的信号低,数据更集中。

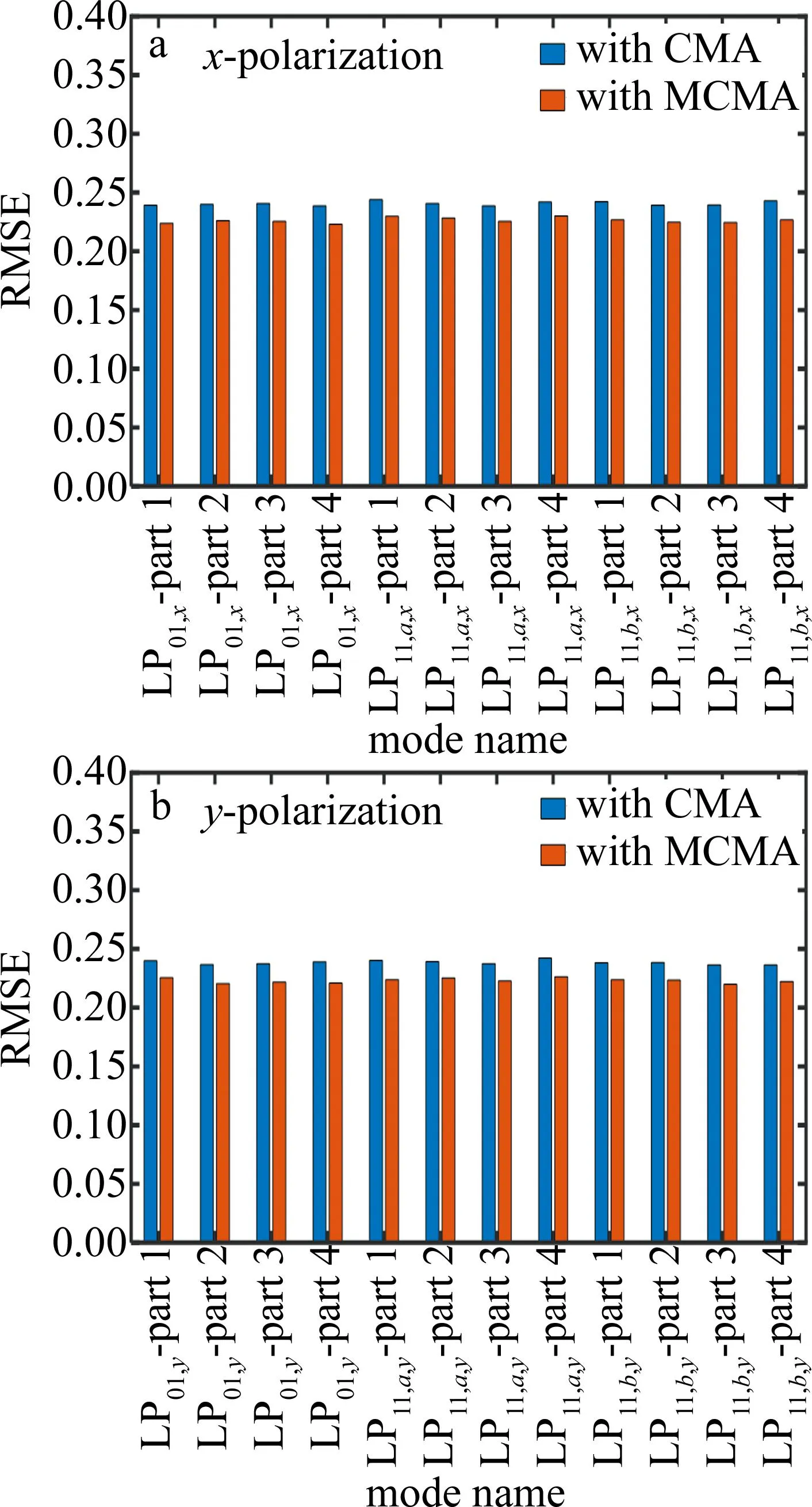
图9 CMA,MCMA均衡后不同模式的RMSE值Fig.9 RMSE values for different modes after CMA, MCMA equalization

图10所示是CMA和MCMA分别用于均衡时,误比特率(bit error rate,BER)随OSNR的变化曲线。在相同的OSNR下,MCMA在误比特率方面优于CMA;对于10-3的误比特率,CMA需要17.5 dB,MCMA需要16.6 dB,即MCMA比CMA提高了0.9 dB。

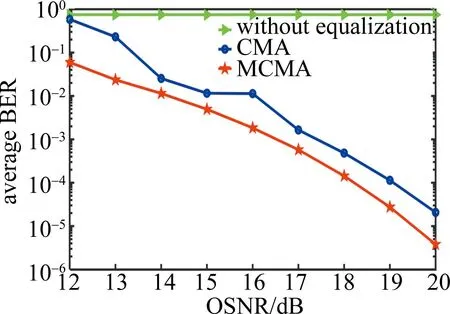
图10 80 km传输距离下平均误比特率与光信噪比Fig.10 Average BER vs. OSNR at 80 km transmission distance

当传输距离增加到120 km,对CMA和MCMA均衡性能进行了比较,如图11所示。随着传输距离的增加,系统误比特率随之增大,但与CMA相比,MCMA仍能提高系统性能。对于10-3的误比特率,CMA需要18.6 dB,而MCMA需要17.6 dB,即MCMA与CMA相比有1.0 dB的改善。

DMGD的大小会影响模分复用系统的信号传输质量。当选定传输距离为100 km,比较了DMGD长度对性能的影响,如图12所示。随着DMGD从130 ps/km增加到260 ps/km,系统性能有所下降,但MCMA在误比特率方面仍然优于CMA。这表明在DMGD方面,MCMA比CMA有更好的均衡性能。

图12 100 km传输距离下平均误比特率与光信噪比Fig.12 Average BER vs. OSNR at 100 km transmission distance

4 结 论

利用VPI仿真平台建立强耦合6×6模分复用系统并传输DP-QPSK信号,在接收端应用CMA和MCMA算法对信号进行均衡,通过增加传输距离和DMGD,比较了CMA和MCMA的均衡效果。结果表明,MCMA的均衡效果优于CMA,主要体现在收敛曲线、RMSE和误比特率方面。与CMA相比,MCMA可以得到较小的稳态误差和较小的RMSE值。此外,对于10-3的误比特率,MCMA与CMA相比表现出约1.0 dB的改善。研究结果还表明,在长距离模分复用系统中,CMA是一种有效的对抗强模式耦合的均衡算法,而MCMA的均衡效果优于CMA。