由2020年海南卷第21题引发研究与思考

李昌成

(新疆乌鲁木齐市第八中学 830002)

一、题目呈现

(1)求C的方程；

(2)点N为椭圆上任意一点，求△AMN的面积的最大值.

二、解法探究

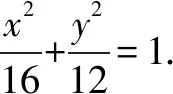
对于(2)，我们可以从不同的角度来思考这个问题，运用解析几何的一些基础知识，采用通解通法即可解答本题.

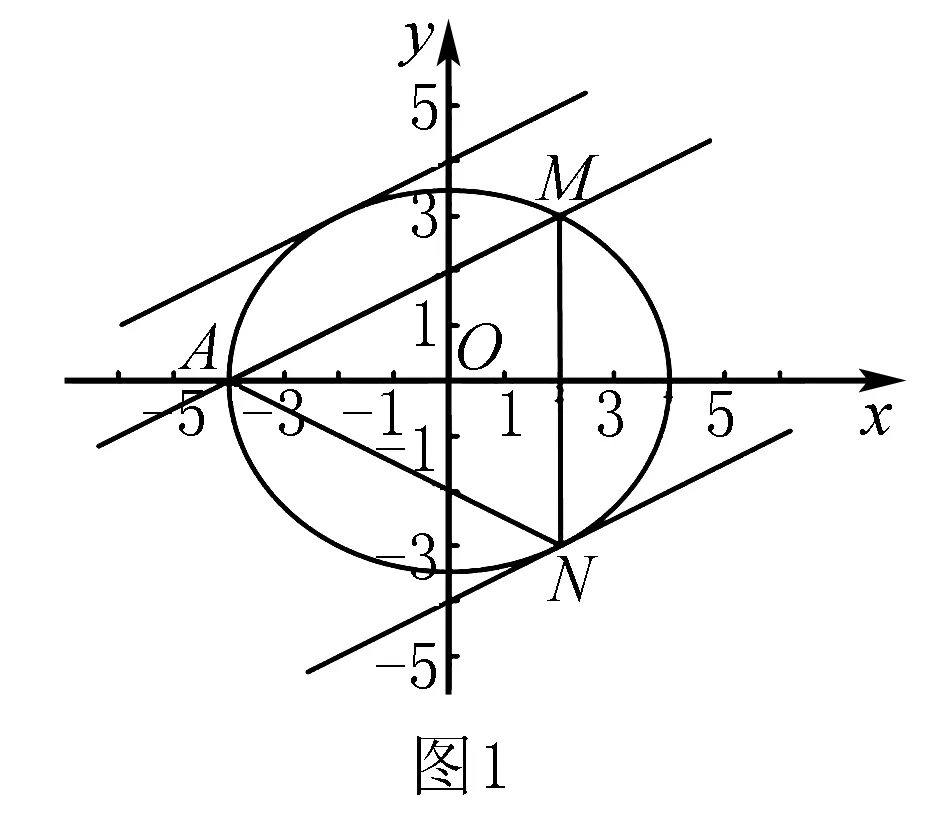
分析1 直线AM的方程易求，进而可计算|AM|的值.要使△AMN的面积最大，就是要使点N离直线AM最远.数形结合可知，点N就是直线AM的平行线与椭圆C在第四象限的切点，如图1.

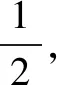
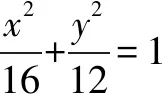
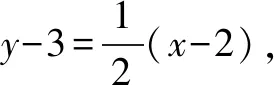
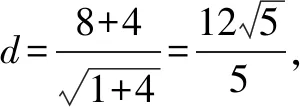
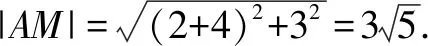
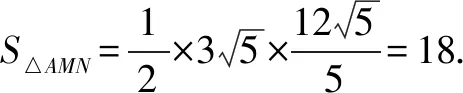
所以△AMN的面积的最大值为18.

评析通过数形结合，能够大致确定取得最值的点N的位置，这是定性分析.通过计算可以精准确定最值.二者结合充分展示了解析结合的基本理念：用代数研究几何.这是学生必须理解掌握的内容.这种解法在2008年全国Ⅱ卷第21题已经考查过.

分析2 本题可以转化为求函数最值问题.椭圆的参数方程可以提供基础支持，利用三角函数可以完成最值的求解.

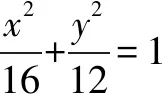
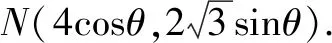
结合解法1，点N到直线AM的距离

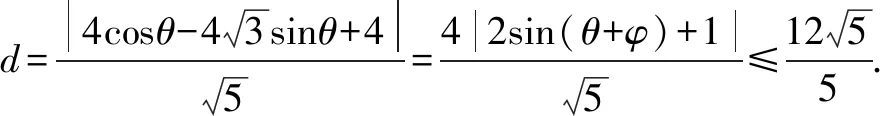
所以△AMN的面积的最大值为18.

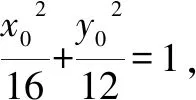
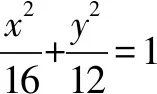
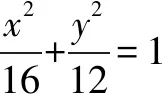
所以△AMN的面积的最大值为18.

评析这是一个容易想到的思路.求交点是解析几何的基本要求，在教材中有专项设计.通过计算能够进一步理解直线与曲线相切时，只有一个公共点.也可省去点N位置的选择.

当发现N(2,-3)使得△AMN的面积取得最大值后，后续的三角形面积计算别有洞天.

分析4 数据背后往往就是位置关系，一些特殊的位置关系就会带来简约的计算方法，通径含有的垂直关系对于三角形面积计算很重要.

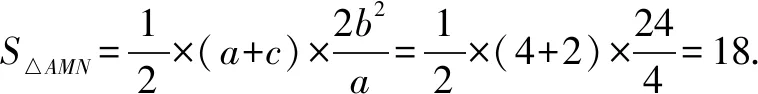
评析充分发掘数据的几何功能让解题变得轻松愉悦，也能感悟到命题者的独到匠心，利用一个特殊的情形对解析几何进行了一般技能技巧的考查.

分析5 对于三角形面积的计算，在必修3《算法初步》一章中介绍了海伦公式，本问题可以用它解答.

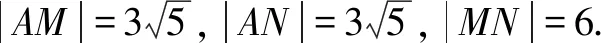
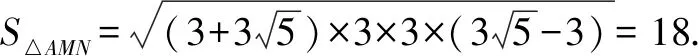
评析海伦公式虽然只是在课本中作为一个算法案例提出，但是它的用法还是很广的，平时教学留意一下，学生普遍能接受.已经多次在高考中考查该知识点.

分析6 在直角三角形中容易计算锐角的三角函数值.含正弦的三角形面积公式也是一个重要的计算方法.

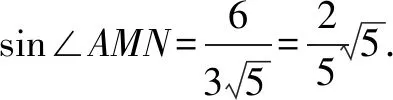
三、背景溯源

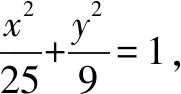
注可类似于解法1解答此题.

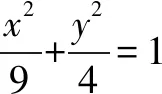
注可类似于解法2解答此题.

(1)求M的方程；

(2)C、D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值.

题源4 (2008年全国Ⅱ卷理科21题)设椭圆的中心在原点，A(2,0)，B(0,1)是它的两个顶点，直线y=kx(k>0)与AB相交于点D，与椭圆相交于E，F两点.

(1)若ED=6DF，求k的值；

(2)求四边形AEBF面积的最大值.

四、几点思考

1.回归教材，回归基础

高考题取材主要来源于教材，正如此题.然而在日常教学中我们发现，普遍存在轻教材，重教辅的情形，无限制地拔高，甚至研究出很多的高深技法，学生学得苦，老师教得累，劳而无功.

2.研究高考真题，把握命题方向

高考题是命题专家们经过周密思考，反复研磨打造出来的精品.从这些题中我们能发现命题的重点、难点、常考点，我们能学到常见的解题方法，重要的技能技巧.让学生把这些将来深造需要的知识掌握扎实即可，切实为学生减负.

3.重质量，轻数量，勤研究

刷题现象在全国各地十分普遍，似乎靠数量取胜.事实上，只有潜心研究，真正弄懂的问题才能在高考时“复制”出来，只有深入研究了才能发现每类问题的最佳解题途径.本例中，显然利用参数方程的解法2最为简洁，既提高了考试的准确率(运算小)，也为考试赢得了宝贵的时间.深入研究还可以让零散的知识有机地串联起来，相互照应，让学生思路开阔，思维灵活，培养真正的创新人才.