一般三角形射影定理及其应用
李秀元
(湖北省武穴市实验高级中学 435400)
一、一般三角形射影定理简介
在三角形ABC中,角A、B、C的对边分别为a、b、c,则a=bcosC+ccosB,b=ccosA+acosC,c=acosB+bcosA.这是人教社课标A版实验教科书必修5《解三角形》的一道练习题,教材本意是要求学生利用余弦定理来证明这组公式,但实际上,它的证明方法可以更简单,作三角形一边上的高,将边长分割成两段,利用直角三角形中锐角的三角函数定义(相当于斜边的射影),直接得到结论.由于证明方法相当于对两边作一边上的射影,故名射影定理,也称第一余弦定理,公式适用于所有三角形.
二、一般三角形射影定理的分类应用举例
解三角形一般直接应用正余弦两大定理和三角恒等变换公式,但有些试题转化起来略显麻烦.而教材例习题及其结论是可以作为高考试题的直接运用,这为一般三角形射影定理的应用带来便利.下面结合高考试题和教材习题,举例说明应用射影定理带来的好处,供大家学习参考.
1.射影定理在求角中的应用
例1 △ABC的内角A,B,C的对边分别为a,b,c,已知a=bcosC+csinB.
(1)求B; (2)若b=2,求△ABC面积的最小值.
说明一般地,对于象a=bcosC+csinB这样的边角关系式,我们总是应用正余弦定理及三角恒等变换公式进行化简,最终得到问题的解.题目几乎没有难度,但有时感觉还是有点繁、费时,毕竟高考是需要抢时间的,一般问题快速求解才能给复杂问题预留时间.合理利用射影定理就能实现抢时目标.所列试题,如果有两问,我们只关注第1问的解法,第2问略过,下同.
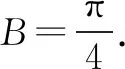
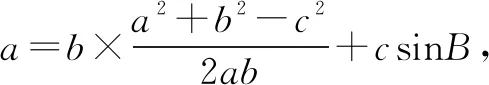
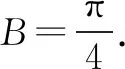
例2 设△ABC的内角A,B,C的对边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
解 方法1对bcosC+ccosB=asinA应用正弦定理,可以得到sinBcosC+sinCcosB=sin(B+C)=sinA=sin2A,从而sinA=1,故三角形△ABC为直角三角形.
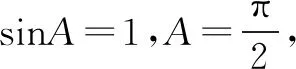


方法2提取公因式sinB后,由射影定理,得
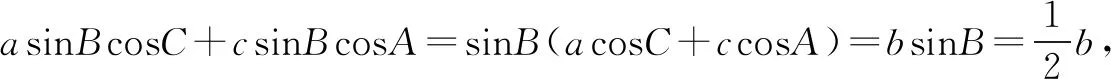
射影定理在化简与求值中的应用



解 方法1基于正弦定理和三角恒等变换公式,

去分母,得sinBcosA-2sinBcosC=2sinCcosB-sinAcosB.

方法2基于射影定理,

整理,得bcosA+acosB=2ccosB+2bcosC,即c=2a.
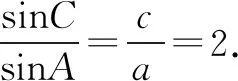

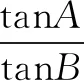
(2)求tan(A-B)的最大值.
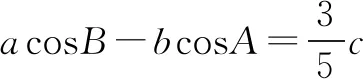
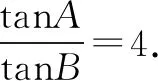
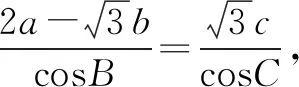
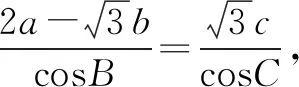
3.射影定理在证明中的应用
例7 在△ABC中,求证:c(acosB-bcosA)=a2-b2.
解 方法1 由余弦定理可得

说明前者套用余弦定理的公式,后者进行了整体代换.
方法2由射影定理,得
c(acosB-bcosA)=(acosB+bcosA)(acosB-bcosA)
=a2cos2B-b2cos2A
=a2(1-sin2B)-b2(1-sin2A)=(a2-b2)+(b2sin2A-a2sin2B)
根据正弦定理,上式后者为0,故c(acosB-bcosA)=a2-b2.
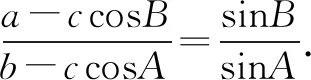
证明 方法1 应用余弦定理化角为边
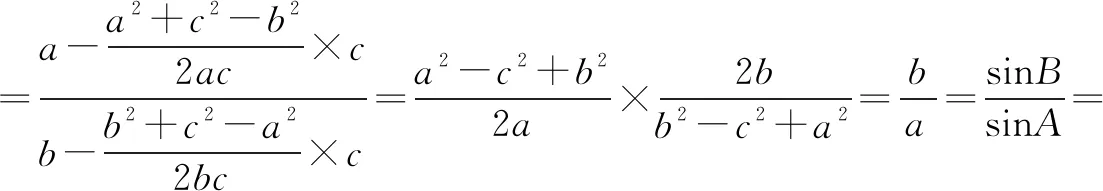
方法2应用正弦定理化边为角
方法3应用射影定理


