关于高中数学中椭圆解题方法研究

况慧珍

(安徽省濉溪中学 235100)

在日常的高中数学解题中，高中生们经常会使用椭圆的相关知识以及解题思路去解决一些相对来说比较困难的问题.椭圆的相关问题不仅仅会经常出现在日常的数学题中，在高考中，也会大量的涉及，由此可见椭圆解题方法的重要性.正是因为如此，高中教师在日常的教学中要着重培养学生们“透过现象看本质”的能力，帮助学生们建立起良好的椭圆问题的解决思路.因此，高中生们应该对与椭圆相关的问题进行剖析，从而真正地掌握椭圆相关知识，并且能够将知识综合地利用起来.

一、有关椭圆解题法的相关例题分析

椭圆解题法是高中生解决相应数学问题的常用方法，高中数学中对于圆锥的定义分为三种，分别为椭圆第一定义、椭圆第二定义，以及从椭圆上两点分别向直径作两条线段与直径的端点处的切线平行，并且两线段的平方等于直径上两条相应线段的乘积之比.通过“焦点线”定义而引出来的椭圆问题也是多种多样的，在实际的解题过程中，如果我们遇到了焦点与椭圆上的点之间的问题时，就可以利用准线定义法来解决.下面本文对这类问题进行了举例分析.

根据以上问题，本文作了相应的辅助线来帮助解题，如下图所示：

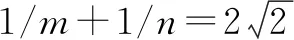
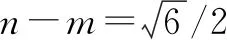
通过完成以上这道例题，我们可以发现，本道题主要是靠椭圆与几何的相关知识来共同完成的，另外在解本题的过程中，不仅仅是利用椭圆的基础知识，同时也利用了代数知识，在未知的情况下先赋值再求解，便于我们的解题.由此，我们在解椭圆相关问题时，可以通过“定位”、“定量”两个方向来进行椭圆方程的确定，其中，“定位”是指通过坐标系来明确出椭圆的焦点.“定量”是指在明确了椭圆所在坐标系中的位置之后，可以通过待定系数法将相应的变量进行代入.

在这道题的解题过程中，也用到了三角形的相似来进行解题，这也锻炼了学生们对知识的综合利用能力.与此同时需要注意的一点是，随着高中数学改革的不断深入，高中数学椭圆相关问题的解题思路将会朝着“向量”的方法进行发展.因为它结合了“数”、“形”两种思想，“数形结合”的方法是高中数学解题过程中经常用到的方法，如果能够将“数形结合”方法与椭圆解题相结合，那么学生们的解题过程将会更加简单方便.因此，本文认为，高中生在数学的学习过程中，要灵活利用“数形结合”这一方法.

二、高中数学椭圆解题法重点

认真审题是解决数学问题时的重要开端.在审题的过程中我们能够从中获取一定的解题关键.题目会告诉我们很多的内容，比如相关的数据、位置等，通过这些已知的信息能够推导出椭圆的方程式；其次，在学习椭圆的相关知识时，学生们要及时地对于知识进行梳理以及记忆.通过相关的调查，我们发现，现阶段高中数学题在不断地将各种知识进行结合，从而考查学生们对于知识的综合运用能力，因此，学生们在进行学习时也要注意将知识进行串联，从而掌握不同层次的知识.

综上所述，高中生们在学习椭圆解题方法的过程中，要将相关的基础知识学得扎实，这样才能为他们将来的解题打下坚实的基础.在通过例题来进入深入研究时，我们发现，要想提升学生们对于椭圆问题的解题能力，单单靠增加做题数量是不够的，同时要增加学们的做题质量，通过一道经典的例题，就能够帮助学生们将相关知识进行运用，从而提升学生们的解题能力以及解题思维.