密实度对垂直轴潮流能水轮机水动力性能影响分析

(江苏科技大学船舶与海洋工程学院，江苏镇江 212003)

随着各行各业发展的需求，传统能源日渐枯竭、环境不断恶化。为缓解这些问题，世界各国政府将目光投向蕴藏着丰富可再生能源的海洋，各国学者也越来越重视对可再生能源的开发利用。潮流能[1-3]由于清洁无污染、可循环利用、能量密度大、不占有陆地资源等明显优势，越来越受到国内外学者们的青睐。水轮机[4]是潮流能电站的关键部件，它的水动力性能直接关系到电站的效益。垂直轴水轮机由于具有与流向无关、结构简单、噪音低等特点，成为学者们研究的重点。流管法[5]、涡方法[6]和CFD 方法[7-8]是垂直轴水轮机水动力性能研究的主要方法，其中CFD 方法由于能够提供详细的流场信息,得到了广泛的应用。

目前大多数垂直轴水轮机都是采用直叶片。因此，在确定叶片翼型情况下，影响水轮机性能的主要参数为水轮机直径、叶片弦长和叶片数等，而体现这3 个参数的无量纲量就是密实度。从现有文献来看，研究密实度对垂直轴水轮机水动力性能影响的比较少，绝大部分都是针对一种具体的垂直轴水轮机形式，研究其在不同条件下的水动力性能。如孙科等[9]针对三叶片垂直轴水轮机自启动性能进行了研究。王凯等[10]研究了不同密实度垂直轴潮流能水轮机的相位干扰，但该文说的不同密实度只是针对叶片数而言，即只改变了水轮机的叶片数。因此，本文基于CFD 方法(ANSYS CFX)，从水轮机直径、叶片数及叶片弦长三个方面考虑密实度的变化，比较系统的研究密实度对垂直轴水轮机水动力性能的影响，得到相应影响规律，为垂直轴水轮机的选型提供相关依据。

1 数值模拟

王凯等[11-12]和SHENG Qihu，et al[13]等已验证了ANSYS CFX 计算垂直轴潮流能水轮机水动力性能的有效性，因此本文基于ANSYS CFX 研究密实度对垂直轴水轮机水动力性能的影响。

2010 年LI Ye，et al[14]研究了垂直轴潮流能水轮机的三维效应对效率的影响，研究表明当叶片的展长与半径的比值大于2 时，三维效应的影响已不是很明显。另外三维效应对不同密实度的水轮机的影响性质是一致的，即二位模型效率高的水轮机，三维模型效率也应该是高的。本文研究的目的是得到密实度对垂直轴水轮机水动力载荷的影响，为垂直轴水轮机的选型提供一定的参考，因此本文采用二维模型模拟水轮机在均匀来流环境中运行的水动力性能。计算模型参数如表1 所示。本文通过滑移网格来实现水轮机的旋转运动。因此，将整个计算域划分为圆形旋转域和外域，如图1 所示。叶片在圆形旋转域内部，叶片的旋转轴位于圆形旋转域的中心。整个计算域长32D，宽16D，且速度入口距水轮机中心8D。

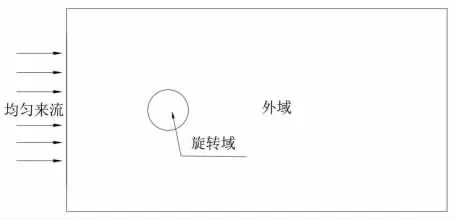
图1 计算域示意图Fig.1 Calculation domain schematic

为了提高计算精度和计算效率，外域和旋转域都采用结构化的网格，叶片表面第一层网格高度0.0001 mm，Y+值基本在5 左右，具体网格模型如图2 所示。

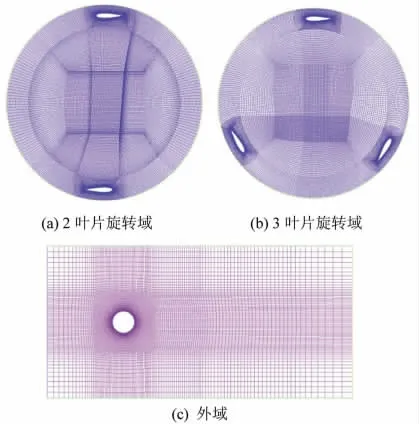
图2 网格示意图Fig.2 Mesh schematic

表1 水轮机模型参数表Tab.1 Principal parameters of the test turbine

垂直轴水轮机在运行过程中，叶片仅做绕定轴的旋转运动，因此运动的控制采用滑移网格的形式，即给出叶片的旋转角速度，保持了计算过程中网格的质量。其他边界条件设置如下：参考气压设为大气压；在进口边界给定来流速度的大小和湍流强度；在出口边界给定相对压力；叶片表面设为无滑移壁面；圆形旋转域和外域之间通过交界面连接；其他边界设为自由滑移壁面。湍流模型选用SST 模型，以水轮机旋转3°所用时间作为时间步长进行瞬态计算。

2 计算结果分析

为方便后续分析，建立如图2 所示的计算坐标系，并定义下述无量纲参数。

式中：λ 为叶尖速比；CFx为水轮机推力系数；CFy为水轮机侧向力系数；CP为能量利用率；ρ 为介质密度；U 为均匀来流速度；R 为水轮机半径；b 为叶片展长；ωT为旋转角速度；FX为水轮机推力，沿坐标系X 轴方向；FY为水轮机侧向力，沿坐标系Y 轴方向；TZ为主轴转矩。

由密实度的表达式可以看出，密实度的变化可以通过改变叶片数、叶片弦长和水轮机直径来实现。因此，下面将从叶片数、叶片弦长和水轮机直径三方面来分析密实度对垂直轴水轮机水动力特性的影响。根据垂直轴水轮机水动力载荷的特点，水轮机旋转一周，水动力载荷是发生波动的，波动的频率是NωT。因此在后续分析时，通过分析水动力载荷的均值和波动幅值来体现密实度对其的影响。均值指的是水轮机旋转一周水动力载荷的平均值；波动幅值指的是水轮机旋转一周水动力载荷最大值和最小值的差值。

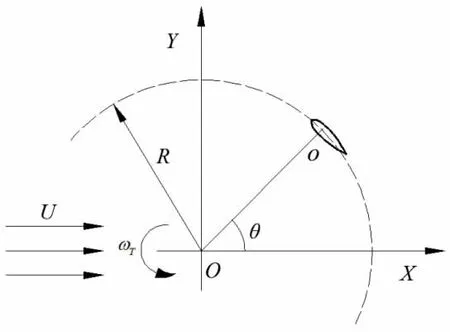
图3 计算模型坐标系Fig.3 Coordinate system of model

2.1 叶片数对水轮机水动力特性影响

为了研究叶片数对水轮机水动力特性的影响，保持水轮机直径(0.8 m)和叶片弦长(0.12 m)不变，选取三种不同叶片数(2、3、4)的水轮机进行数值计算。不同速比下的能量利用率、推力系数和侧向力系数随密实度的变化曲线如图4 所示。图中横坐标密实度的变化仅由叶片数改变引起。

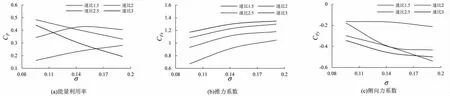
图4 不同速比下水动力载荷系数随密实度的变化曲线Fig.4 The curves of hydrodynamic force coefficient with density under different speed ratio

从图4 可以看出，对于能量利用率而言，在低速比(1.5)时，能量利用率是随叶片数的增加而逐渐增加的；在高速比(2.5、3)时，随着叶片数的增加，能量利用率却逐渐减小，这主要是由于叶片之间的干扰引起的。对于推力系数而言：随着密实度的增加，推力系数逐渐增加。对于侧向力而言：随着叶片数的增加，侧向力系数绝对值基本上也是逐渐增加的，只是在不同速比，增加的速率有所变化。

表2 不同叶片数下水动力载荷波动范围Tab.2 The fluctuation ranges of hydrodynamic load under different blade numbers

设计垂直轴水轮机时，经常尽量使水轮机的能量利用率达到最大，从图4(a)可以看出，不同叶片数(密实度)下，基本上都是在速比2 或2.5 时，能量利用率达到最大。因此，表2 给出了速比2 和2.5 时，水动力载荷在不同叶片数下的波动范围。从表中可知，在速比2 和2.5 时，随着的叶片数(密实度)的增加，能量利用率、推力系数和侧向力系数的波动范围均逐渐减小。所以，随着叶片数的增加，水动力载荷的波动频率逐渐增加，但波动幅值迅速减小。波动频率的增加不利于水轮机结构的疲劳寿命，但波动幅值的减小有利于电能输出的控制和结构的设计。

2.2 叶片弦长对水轮机水动力特性影响

为了研究叶片弦长对水轮机水动力载荷的影响，保持水轮机直径(0.8 m)和叶片数(3 m)不变，选取3 种不同叶片弦长(0.09 m、0.12 m、0.15 m)的水轮机进行数值计算。不同速比下的能量利用率、推力系数和侧向力系数随密实度的变化曲线如图4 所示。图中横坐标密实度的变化仅由叶片弦长改变引起。

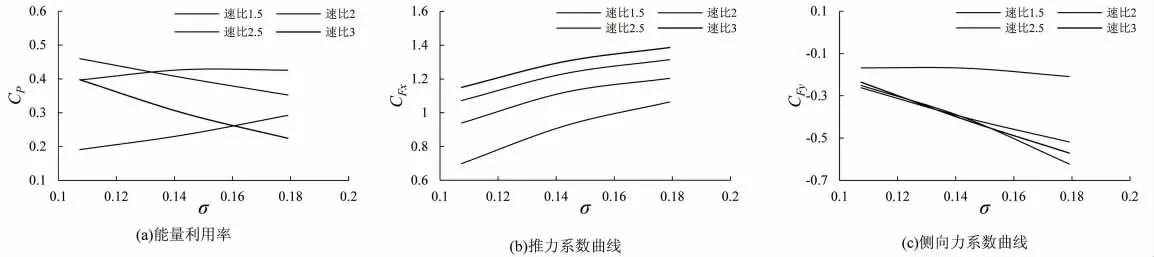
图5 不同速比下水动力载荷系数随密实度的变化曲线Fig.5 The curves of hydrodynamic force coefficient with density under different speed ratio

从图5 可以得到2.1 节一致的结论，即对于能量利用率而言，在低速比(1.5)时，能量利用率是随叶片弦长的增加而逐渐增加的；在高速比(2.5、3)时，能量利用率随着叶片弦长的增加逐渐减小。对于推力系数而言：随着叶片弦长的增加，推力系数逐渐增加。对于侧向力而言：随着叶片弦长的增加，侧向力系数绝对值基本上也是逐渐增加的，只是在不同速比，增加的速率有所不同。

同样，从图5(a)可以看出，不同叶片弦长(密实度)下，能量利用率都是在速比2 或2.5 时达到最大值。因此，表3 给出了速比2 和2.5 时，水动力载荷在不同叶片弦长下的波动范围。从表中可知，随着的叶片弦长(密实度)的增加，在速比2 时，能量利用率的波动幅值逐渐减小；而在速比2.5 时，能量利用率的波动幅值逐渐增加。对于推力系数和侧向力系数而言，不管在速比2 还是2.5 时，波动范围随叶片弦长(密实度)的增加均逐渐增加。所以，增加叶片弦长对于水轮机的结构安全是不利的。

表3 不同叶片弦长下水动力载荷波动范围Tab.3 The fluctuation ranges of hydrodynamic load under different chord lengths

2.3 水轮机直径对水轮机水动力特性影响

为了研究水轮机直径对水轮机水动力载荷的影响，保持水轮机叶片弦长(0.12 m)和叶片数(3 m)不变，选取三种不同水轮机直径(0.6 m、0.8 m、1.0 m)的水轮机进行数值计算。不同速比下的能量利用率、推力系数和侧向力系数随密实度的变化曲线如图4 所示。图中横坐标密实度的变化仅由水轮机直径改变引起。

图6 不同速比下水动力载荷系数随密实度的变化曲线Fig.6 The curves of hydrodynamic force coefficient with density under different speed ratio

从图6 同样可以得到与2.1 节一致的结论，即随水轮机直径的减小，在低速比时，能量利用率逐渐增加的；而在高速比时，能量利用率却逐渐减小。推力系数和侧向力系数绝对值随直径的减小基本上都是逐渐增加的，只是在不同速比，增加的速率有所不同。

同样，从图6(a)可以看出，不同水轮机直径下，能量利用率都是在速比2 或2.5 时达到最大值。因此，表4 给出了速比2 和2.5 时，水动力载荷在不同直径下的波动范围。从表中可知，随着的直径的增加，在速比2 时，能量利用率的波动幅值逐渐增加；而在速比2.5 时，能量利用率的波动幅值逐渐减少。对于推力系数和侧向力系数而言，不管在速比2 还是2.5 时，波动范围随直径的增加均逐渐减小。所以，增加水轮机直径对于水轮机的结构安全是有利的。

表4 不同叶片直径下水动力载荷波动范围Tab.4 The fluctuation ranges of hydrodynamic load under different diameters

3 结论

本文从三个方面考虑密实度的变化，并计算分析了密实度对均匀来流中二维垂直轴水轮机水动力载荷的影响，研究结果表明：

(1)在低速比时，能量利用率均值随密实度的增加逐渐增加；而在高速比时，其随密实度的增加逐渐增小。

(2)推力系数和侧向力系数均值均随密实度的增加而增加。

(3)仅由叶片数增加导致密实度增加时，能量利用率、推力系数和侧向力系数的波动幅值均逐渐减小。

(4)仅由叶片弦长增加或水轮机直径减小导致密实度增加时，能量利用率波动幅值在不同速比变化规律有所不同，但推力系数和侧向力系数的波动幅值均逐渐增加。